粉末增材制造微结构的非等温相场模拟

杨阳祎玮，易敏，胥柏香

(1.达姆施塔特工业大学材料与地质科学系，德国达姆施塔特，D-64287；2.南京航空航天大学航空学院，江苏南京，210016；3.南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京，210016)

粉末增材制造技术具有材料浪费少、零件结构设计自由、加工工序少、加工周期短、易于实现形状复杂零部件快速成型等特点，在航空航天、医疗仪器、轨道交通、新能源等战略新兴产业领域具有重大价值和广阔的应用前景，是先进制造和智能制造的重要发展方向[1]。粉末增材制造的零部件性能与增材制造过程中形成的微结构密切相关。通过计算模拟预测粉末增材制造过程中微结构及其演化与增材制造参数之间的关联规律，对准确把握增材制造过程的材料-工艺-微结构-性能关系，实现增材制造参数的高效低成本设计与优化，具有重要意义[2-4]。因此，以微结构演化为核心的增材制造建模与计算，已成为基于增材制造的材料/结构设计和开发过程的重要组成部分。

粉末增材制造中微结构演化及形成的影响因素极其复杂，涉及粉末与高能集中热束(激光、电子束或电弧等)的相互作用、传热与传质、相变、晶粒生长、熔体流动、结构弛豫等多种物理过程[5-7]，如何考虑这些多物理过程及其强耦合是粉末增材制造建模及计算的关键。针对粉末增材制造过程中上述物理过程的模拟已经开展了一些研究。比如，对于熔化过程以及熔体流动，常采用基于有限元和有限体积法的计算流体动力学方法，以及格子玻尔兹曼(Lattice Boltzmann method,LBM)方法，可涵盖固液相变、反冲压力、Marangoni 对流、毛细作用力等现象；对于晶粒生成及长大，可采用元胞自动机(cellular automata,CA)方法；亦可将格子玻尔兹曼方法与元胞自动机方法耦合，实现熔化与晶粒生长的模拟。这些方法在模拟增材制造的1个或几个物理现象方面取得了很好的效果，但如何在模型中全面融入多个物理过程及其耦合仍是增材制造建模与计算的挑战，而相场模型在这方面展现了一定潜力与优势。相场模型可采用序参量描述气/液/固相、晶粒形状/取向、铁电/磁畴等各种复杂的微结构，用连续光滑的函数描述不同微结构之间的界面，并能方便地直接引入描述各种物理过程的场变量(如应力/应变、熔体流速、温度、浓度、电/磁场等)，序参量在时间和空间上的演化即能表征微结构及其界面的动力学过程。目前，在采用相场模型应用于增材制造模拟方面，研究人员开展了初步探索研究。CHOU等[8]以温度梯度和凝固速度为输入参数，采用等温相场模型计算了增材制造中枝晶形貌的变化过程；KRIVILYOV 等[9]将多相流模型和相场模拟结合，研究了粉末固结行为，但未直接考虑增材制造过程的温度场信息；ZHANG 等[10]直接采用等温相场模型计算了多种金属粉末的增材制造过程，但并未考虑热传导和与非等温过程相关的微结构特征。最近，LU 等[11]在相场模型中综合考虑了气/液/固相、粉末熔化、熔体凝固和晶粒生长，并且直接在粉末尺度考虑了含热束热源的热传导方程与相场演化方程的耦合，基于该模型的二维计算可重现增材制造试验中的许多微观结构特征，但该模型并未考虑熔池的流体动力学及其对微结构的影响。

针对粉末增材制造模拟所面临的问题和不足，以及粉末与高能集中热束作用产生的极大温度梯度和非平衡过程，本文作者改进粉末增材制造的非等温相场模型，全面考虑热传导、熔体流体动力学、微结构演化三者之间的耦合，并将该模型有限元数值化后应用于模拟316L 不锈钢粉末非等温烧结、选取烧结和选区熔化增材制造，研究热束功率和扫描速度对孔隙率、表面形貌、温度分布、晶粒形状及取向、致密度等微观结构特征的影响规律，通过深入了解粉末增材制造过程中的“工艺参数-微观结构-材料性能”基本关系，为目前以实验试错为主要模式的粉末增材制造领域提供借鉴和指导。

1 相场模型简介

相场模型采用空间连续变化的序参量来描述微结构，是一种扩散界面模型，不同微结构间的界面采用序参量的光滑函数来描述，界面是非突变的。传统突变界面模型中，描述问题的偏微分方程的定域是移动的，一系列偏微分方程通过移动且未知界面上的边界条件进行耦合，需显式跟踪界面位置，难以处理复杂及弯曲界面，数值计算存在一定困难。相场模型的界面光滑连续避免了突变界面模型的困难，序参量求解后即可自动捕捉界面位置，方程之间(无需显式地通过界面)自动耦合，从而大大简化数值实现的困难，在模拟材料内部复杂微结构演化方面具有独特优势。相场本质上为基于能量及其变分的一种建模方法。鉴于能量概念的普适性，相场建模被广泛用于处理不同物理及其耦合的问题[12-14]。

相场模型主要有3个要素：一是描述微结构的序参量φ；二是描述微结构系统的能量泛函Ψ；三是描述序参量的动力学方程。相场模型的能量泛函一般可表示为

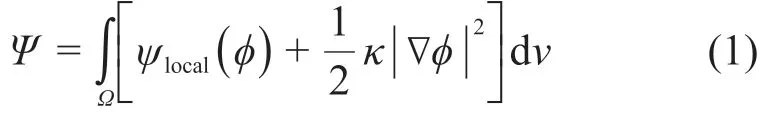
其中：ψlocal(φ)为体(局部)能量密度，为梯度(非局部)能量密度。若ψlocal取双势阱函数4Δgφ2(1-φ)2，且Δg为能量密度壁垒高度，ψlocal的局部极小值φ=1和φ=0分别代表2种不同的微结构，则在平衡条件(即变分偏导δΨ/δφ=0)下可得到实验可测量物理量(界面厚度l和界面能G)与相场模型参数(能量密度壁垒高度Δg和梯度能量密度系数κ)之间的关联如下：

式(2)提供了根据实验数据确定相场模型参数的一种可能。

微结构的演化受控于热动力学，相应地，相场中序参量的演化可以从热动力理论中导出。序参量演化方程可以通过能量泛函对其的变分来描述，根据物理本质的不同，其具体表达式也有所不同。相场模型的序参量及其动力学方程的类型如表1所示[15-18]。目前广泛应用的场变量主要有3类：第一类是不满足守恒条件的非保守场变量，比如铁电极化场、晶粒取向场、气液固相场、裂纹场、马氏体/奥氏体变体场等，主要采用Allen-Cahn方程(也称之为时间相关的Ginzburg Landau方程)来描述其动力学；第二类是满足守恒条件的保守场变量，即总量在微结构演化中始终保持不变，比如各种类型的浓度等，主要采用Cahn-Hilliard方程来描述其动力学；第三类是磁材料中基于微磁学理论的磁化场变量，与前2种常用的保守场和非保守场变量不同，在等温演化过程中磁化矢量场Mm的大小保持恒定，只有方向发生改变，主要采用Landau-Lifshitz-Gilbert方程来描述其动力学。随着更多未涉及的物理过程或问题的出现，可能需要引入新类型的场变量，并推导相应的动力学方程。

表1 相场模型的序参量及其动力学方程的类型Table 1 Type of order parameters and their kinetics in phase-field model

2 非等温相场模型建立

粉末增材制造非等温相场模型如图1所示。粉末增材制造过程包含熔化、凝固、晶粒生长、熔体流动、气泡运动、烧结、热对流、热毛细、热泳等多种复杂的物理现象。为了描述这些现象，本文的相场模型采用了如图1(b)所示的序参量，其中，ρ是保守场变量，描述气孔/空隙(ρ=0)和熔化液体/晶粒等实体(ρ=1)；φs和φl是非保守场变量，分别描述固相和液相；{ηj}(晶粒/粉末颗粒编号j=1,2,3,…,N)是非保守场变量，描述晶粒和粉末颗粒的取向。当ρ=0 时，所有非保守场变量φs，φl和ηj皆取0；当ρ=1 时，φs和φl中只有1 个取1。因此，ρ，φs和φl之间存在如下约束关系：

因此，可用场变量φ来代表固相(φs)，而用ρ-φ来代表液相。

图1 粉末增材制造非等温相场模型Fig.1 Phase-field model of powder-based additive manufacturing

此外，在气孔/空隙和液相条件下无晶粒和粉末颗粒的存在，故而无取向分布，即ηj全取0。在固相条件下才有晶粒取向，因此，只有当ρ=1和φ=1时，第j个晶粒/粉末颗粒的ηj才可取1，而其余ηi（i≠j）皆取0。因此，φ和{ηj}之间存在如下约束关系：

根据以上序参量的选择，基于YANG 等[6,19-20]的研究，粉末增材制造非等温相场模型的能量泛函可构造为：

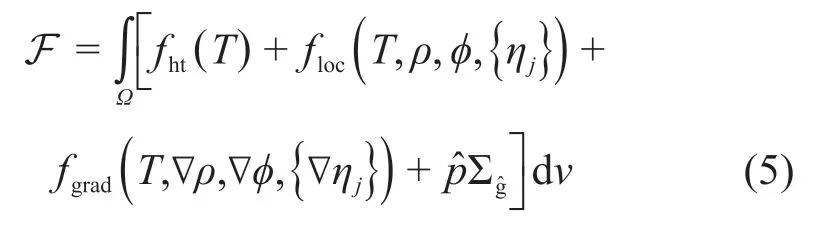
其中：

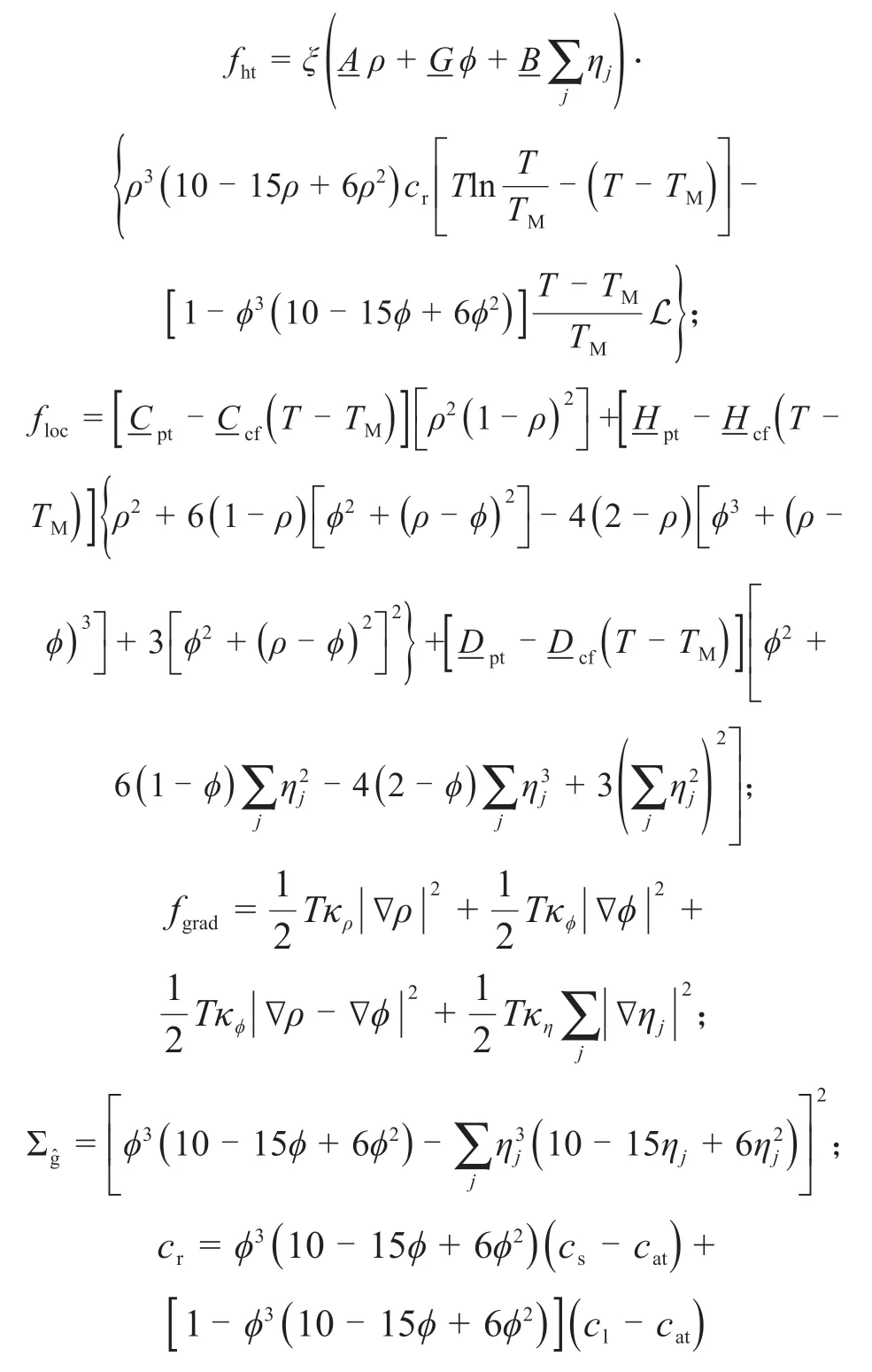
式中：fht为热量贡献的自由能密度，floc为相场模型的局部自由能密度，fgrad为相场模型的梯度自由能密度，此三者皆为温度T的函数；ˆ和Σgˆ分别为约束因子和约束函数；L 为固液相变潜热；TM为熔点；cs，cl和cat分别为固相、液相和气孔/空隙的体积比热容；和κη为模型参数，可根据实验数据拟合得到，ξ为拟合系数。依照惩罚函数法，约束因子ˆ通常赋予一个足够大的值，使约束条件得以满足。

基于以上能量泛函可推导出控制序参量、温度场和流动速度场演化的动力学方程，主要包括以下方程。

熔体流动的控制方程：

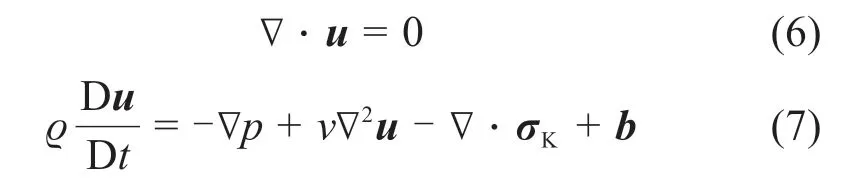
其中：ϱ为密度；u为流动的速度场；p为静水压；v为动力黏性系数；b为质量力；σK为Korteweg 应力张量，其表达式为

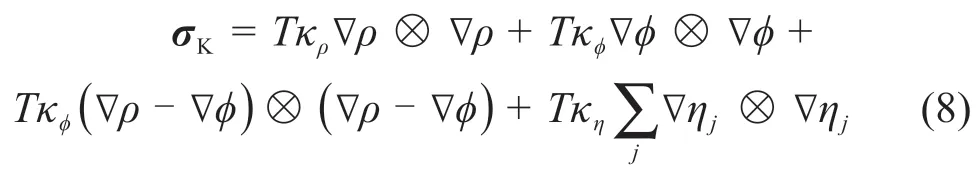
描述温度T演化的热传导方程为

式中：k为热导率张量；为Cauchy应力张量；qv为粉末增材制造过程中高能集中热束的体积功率密度；e为内能密度，

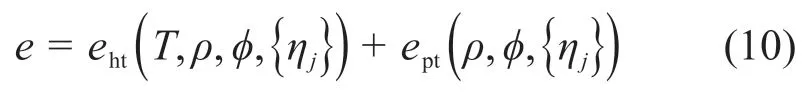
其中：

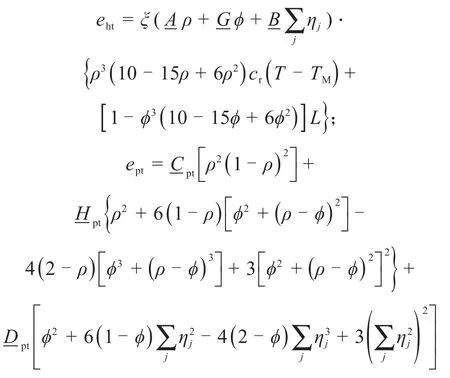
与自由能密度相对应，eht体现了热量对内能的贡献，ept体现了局部势能对内能的贡献。

控制保守场变量ρ演化的方程为

其中：M为对应扩散传质的迁移率张量；Mth为对应热泳传质的迁移率张量。

控制非保守场变量φ演化的方程为

控制非保守场变量ηj演化的方程为

粉末增材制造非等温相场模型的主要控制方程与等温相场模型的差异主要表现在以下几个方面。1)在传质现象方面，传统等温相场模型的Cahn-Hilliard 方程仅含有满足Fick 定律的扩散项，而本文的非等温相场模型还包含温度梯度导致的热毛细和热泳传质效应；2)在熔体流动方面，Korteweg 应力张量是温度相关的，其梯度亦包含了热毛细作用；3)在固液相变及相界面移动方面，在本文的非等温相场模型中，温度梯度额外引入了相界面移动的驱动力；4)在晶界移动方面，温度梯度额外引入了晶界迁移的驱动力；5)本文的非等温相场模型的6个控制方程是相互非线性耦合的；6)对qv的具体表达式进行设计，可模拟基于不同高能集中热束(激光电子束或电弧等)的粉末增材制造，图1(c)所示为增材制造中热束和粉床作用后的能量效应的分布函数qv的基本表达式。

3 微结构演化的非等温相场模拟

为了将上述非等温相场模型应用于具体的粉末增材制造模拟，对该模型进行了有限元编译并应用MPI 并行算法求解，主要是在开源代码MOOSE框架下编写了有限元子程序，采用三维八节点双线性六面体等参单元或二维四节点双线性四边形等参单元，Cahn-Hilliard方程采用分离法求解(引入化学势μ=δF/δρ为额外的自由度)，时间离散采用隐式后向欧拉法，非线性方程组的求解采用预处理的JFNK(Jacobain-free Newton-Krylov)迭代法，采用h型自适应网格技术对序参量急剧变化的界面处网格进行实时加密，而在序参量基本恒定的远离界面处采用较稀疏的网格，降低计算量。对于熔体流动控制方程的求解，对流项采用流线迎风Petrov-Galerkin格式进行稳定，不可压条件采用压力稳定Petrov-Galerkin格式。下文简要概述相关重要步骤及部分计算实例，具体细节可参照文献[6,19-20]。以下实例中除非等温烧结外，均使用了316L 不锈钢作为粉末材料以及氩气作为环境气氛，温度相关的主要材料参数如表2所示。

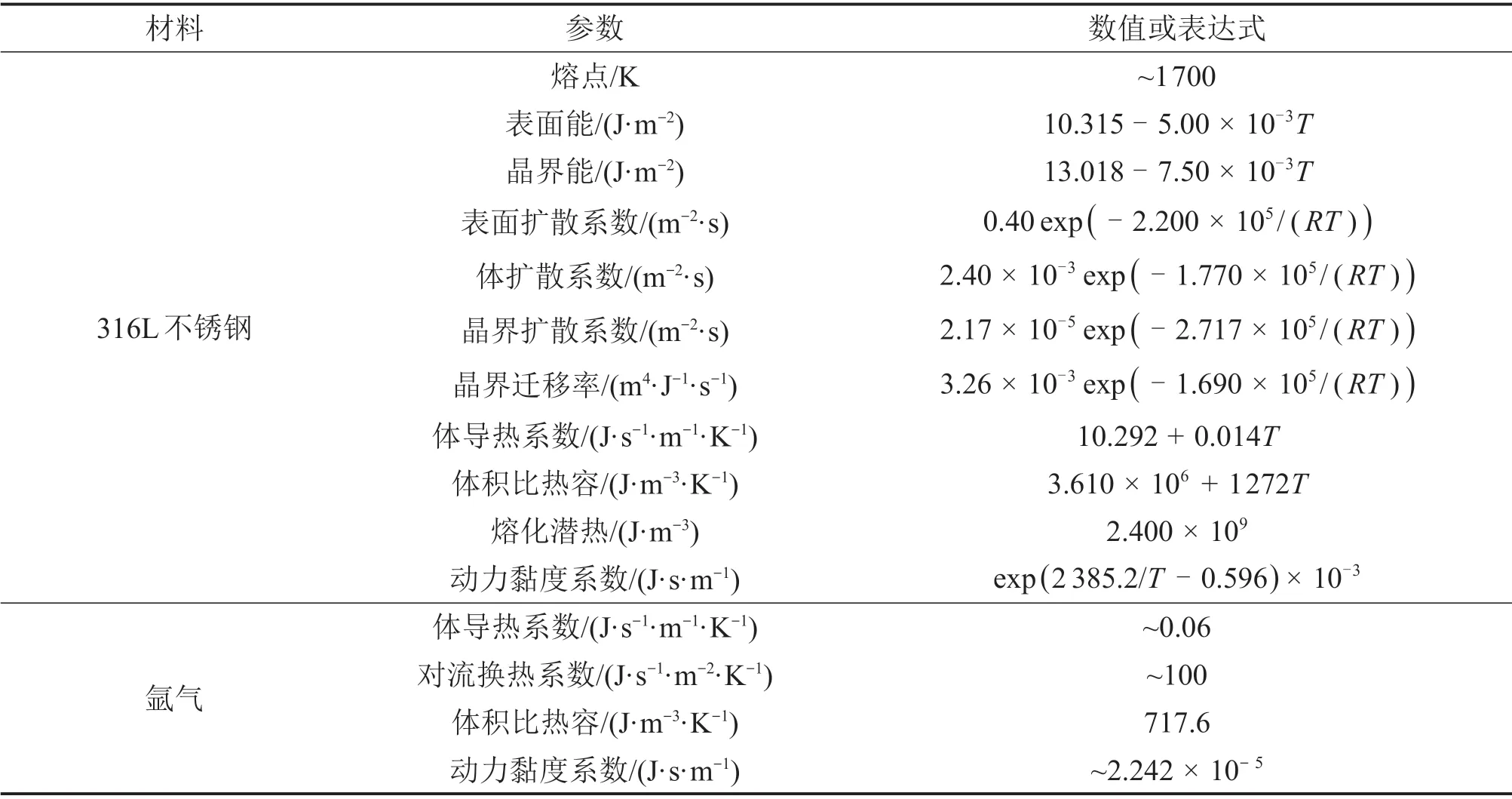
表2 模拟实例中所使用的温度相关的材料参数Table 2 Temperature-dependent material properties used in simulations

3.1 粉床的生成

粉末增材制造模拟的关键步骤之一是粉床生成，本文采用离散元方法来铺设粉床。首先，创建一个疏松堆垛的球形/圆形颗粒集，颗粒间无接触，且颗粒的粒径分布可控；然后，在每个颗粒上施加重力场，使所有颗粒在立方/矩形控制区内平铺开来，直至每个颗粒在重力场和接触力共同作用下到达力学平衡，如图2(a)所示。粉床生成之后，记录每个颗粒i的中心点坐标值r0和半径Ri，标记为顶点vi(r0,Ri)，并将其添加至顶点集合进一步优化。为了减少描述晶粒取向的序参量ηj的数量并降低计算量，采用一种基于Welsh-Powell迭代的最小着色近似算法，结合晶粒追踪方法，可仅用8 个序参量ηj来模拟具有多达200 个晶粒的系统，如图2(a)所示。多层粉末增材制造模拟则是在单层模拟的基础上，将结果形貌以三位多边形网格模型或体素模型的形式重载入到离散元模拟环境下，进行下一层粉床的铺设。完成铺设后，下一层颗粒以及上一层晶粒模拟结果将被同时映射到有限元网格中，在保留上一层晶粒编号的情况下，运行最小着色近似算法进行自由度分配与新颗粒的编号，并进行相参数初始化以进行后续的相场模拟。这一流程随着逐层铺粉将不断重复直至多层模拟结束，如图2(b)所示。

3.2 非等温烧结

在粉末的非等温烧结过程中，温度还不够高，粉末颗粒无法全部熔化，只有颗粒表面发生局部熔化，颗粒之间通过熔化的表面而结合成致密的实体。在这种情况下，本文将不考虑熔体的呈现，即略去序参量φ的控制方程和熔体流动的控制方程，而将表面局部熔化等效为较高的局部扩散系数。图3(a)～(d)所示为2 个相同颗粒的烧结凝聚过程，其中图3(a)所示为传统等温相场模型的结果，可以发现：2 个颗粒的形状在烧结过程中完全等同，且晶界始终位于对称面；而图3(b)～(d)所示为本文非等温相场模型的结果，施加的水平方向温度梯度为10 K/μm。从图3(b)～(d)可以发现：在低温端的晶粒逐渐缩小，而高温端的晶粒逐渐长大，晶界逐渐往低温端移动，2 个颗粒逐渐聚结为1 个椭圆形颗粒，晶界消失，最后在稳态时接近1个圆形颗粒，且颗粒位置靠近高温端。

图3(b)，(c)和(d)所示分别为只考虑热毛细传质、只考虑热泳传质和两者皆考虑条件下的微结构演化过程，可见，温度梯度能大幅加速2个颗粒的烧结凝聚过程。图3(e)和(f)进一步给出了等温相场模型和非等温相场模型中2个颗粒的烧结颈形成率和收缩率随时间的变化关系。从图3(e)和(f)可以发现：对于等温相场模型，当2个颗粒的烧结颈形成率到达最大值时，收缩率立即停止增长，且无晶界迁移发生；而对于非等温相场模型，当烧结颈形成率降至0 时，收缩率出现第二次突变式增加，表明从椭圆形颗粒到近似圆形颗粒的转变。图3(g)所示为YSZ粉堆在1个体积为403μm3，初始温度梯度为10 K/μm的三维孤立系统下进行烧结的微结构演化过程。该粉堆由直径为5～15 μm的颗粒随机紧密堆垛而成，模拟参数可参考文献[20]。图3(h)所示为该粉堆在不同时刻和不同位置的相对密度变化规律。模拟结果显示，在给定热泳传质迁移率Mth的情况下，物质逐渐由较低温度区域向较高温度区域迁徙，使得较高温度区域的相对密度随时间进行而逐渐增加。图3(g)中由温度梯度驱动与化学势驱动的传质流量的相对大小和方向亦反映出温度梯度驱动机制在非恒温烧结过程中对物质传递以及空间再分布有着区别于传统Fick 扩散传质(即化学势驱动)机制的显著作用[20]。

图2 多层粉床生成及逐层增材制造Fig.2 Multilayer powder bed generation and layer-by-layer additive manufacturing

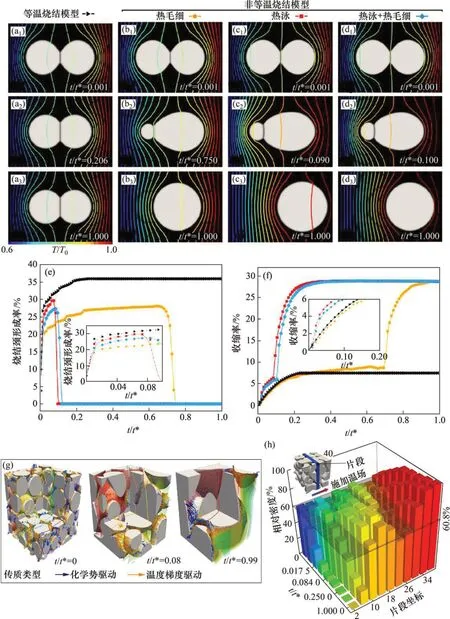
图3 直径20 μm的YSZ颗粒在温度梯度10 K/μm下的非等温烧结的相场模拟Fig.3 Phase-field simulation of non-isothermal sintering of YSZ particles with diameter of 20 μm at temperature gradient of 10 K/μm

3.3 选区烧结(selective sintering，SS)

选区烧结是一种典型的粉末增材制造技术，热束以一定的功率和扫描速度对粉床进行加热，实现逐层烧结成型。316L 不锈钢粉床选区激光烧结的三维模拟在1 个长×宽×高为500 μm×250 μm×65 μm的封闭系统下进行，其底部边界仅允许通过1 个假想的厚度为1 000 μm 的316L 不锈钢衬底进行稳态导热换热，其余边界均允许对流散热。衬底底部、预热以及环境温度均设置为316L 不锈钢熔点的40%，即680 K。除热泳项外，所采用的非等温相场模型与3.2节中的一致，仅需将热束效应作为功率体积密度引入热传导方程[19]。图4(a)所示为功率20 W 和扫描速度100 mm/s 时316L 不锈钢粉床的微结构演化过程；图4(b)所示为激光点附近区域的典型物理现象，包括晶粒生长、扩散、烧结颈形成、局部熔化、传热、温度梯度场等等。可以发现，在高于熔点的过热区域，颗粒表面发生了局部熔化，故而表面能或表面毛细压强会急剧降低，使得表面局部熔体从凸面向凹面流动，这种局部熔体流动会使得冷却时形成一连片的粗晶粒。在局部熔体附近的固体区域，温度依然足够高，这有助于快速扩散，导致相邻颗粒间的缩颈行为。从图4(a)可估算出局部熔化区域和气孔/空隙附近的温度梯度分别高达50 和100 K/μm，如此巨大的温度梯度可导致表面能的非均匀性，进而诱发额外传质，这与等温烧结明显不同。图4(c)和(d)所示为非等温相场模拟的表面微观形貌与实验结果的对比，可以发现两者之间高度吻合，表明了该相场模型的有效性。

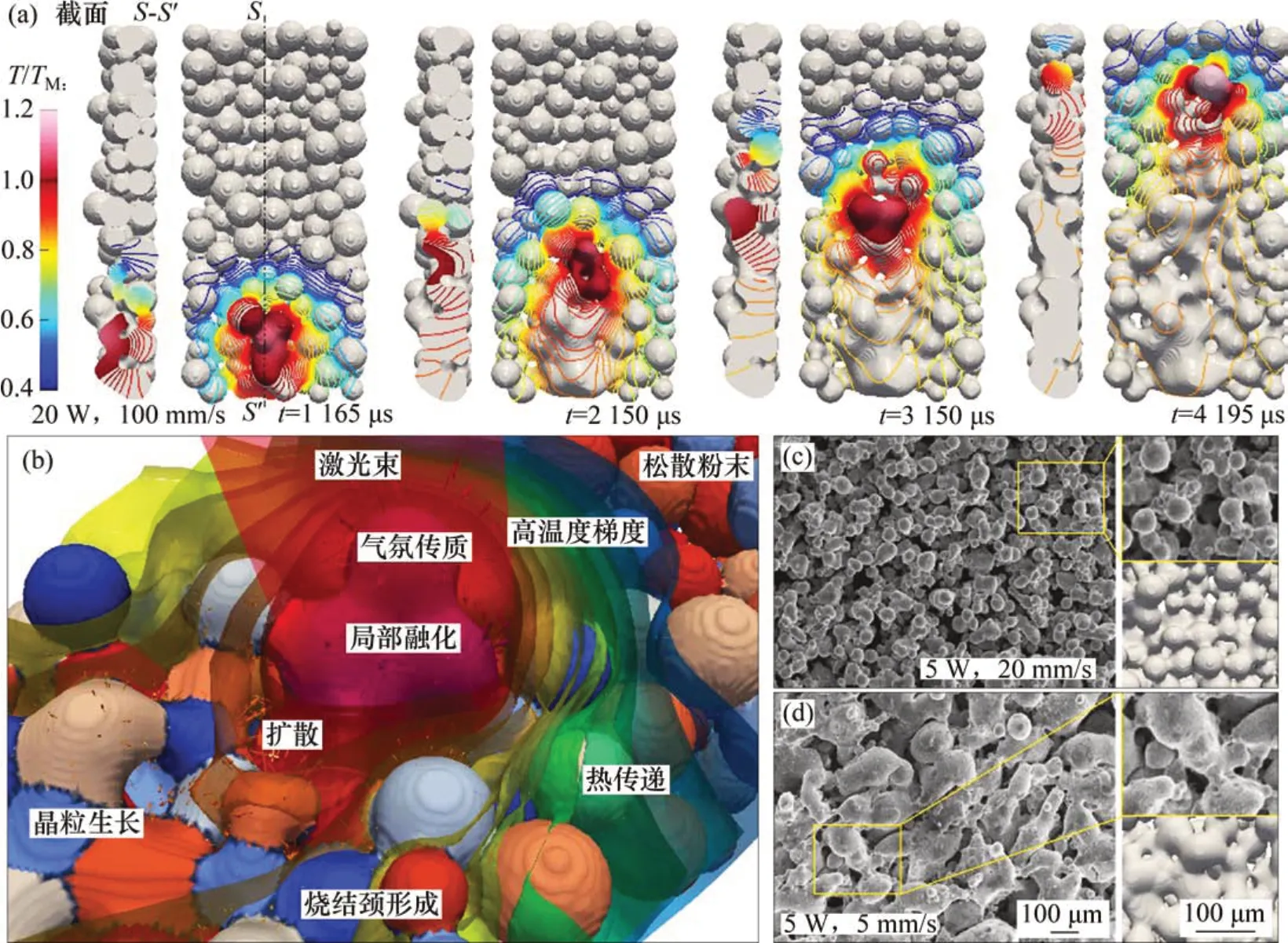
图4 316L不锈钢粉末选区激光烧结的相场模拟Fig.4 Phase-field simulation of selective laser sintering of 316L stainless steel powder

基于大量计算结果的统计，得出激光功率P和扫描速度v对选区激光烧结微结构特征的影响，如图5所示。当点(P,v)位于图5(a)右下角区域时，很多颗粒未聚结，产生较大的孔隙率；当点(P,v)位于图5(a)左上角区域时，颗粒聚结且连续成片，形成较高的致密度。进一步由图5(a)可以看出，固定激光功率时降低扫描速度，或固定扫描速度时增加激光功率，均可提高致密度，降低孔隙率。对图5(a)进行量化分析可以发现，当激光功率和扫描速度之间大概满足关系式P-0.15v-23＞0 时，选区激光烧结316L 不锈钢粉床形成的实体将具有大于90%的致密度，这为选区激光烧结粉末增材制造的激光参数优化及选择，提供了重要参考。

3.4 选区熔化(selective melting，SM)

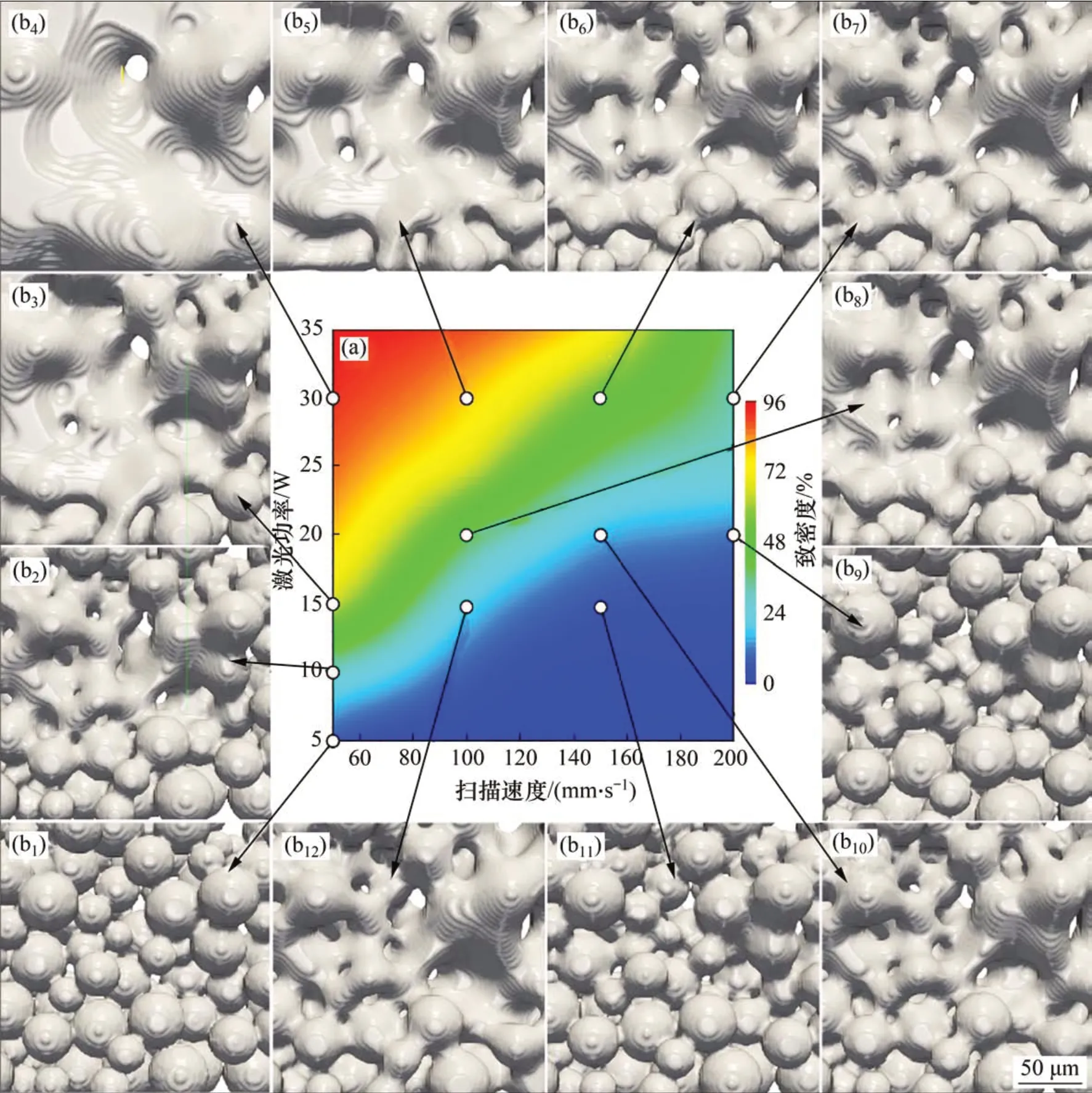
图5 选区激光烧结316L不锈钢粉末的致密度及微结构随激光扫描参数的变化Fig.5 Densification factor and microstructure of selective laser sintering of 316L stainless steel powder under different laser scanning parameters

与选区烧结不同，选区熔化过程的温度更高，可导致大片区域的颗粒发生大面积熔化，并伴随有凝固和晶粒生长过程，故需在非等温相场模型的基础上全面考虑固液相变和熔体流动，最终结果则是第2节中所展示的热-熔体-微结构耦合非等温相场模型。316L 不锈钢粉床选区激光熔化的二维模拟在1 个长×宽为1 000 μm×500 μm 的封闭系统下进行，其底部边界仅允许通过1个假想的厚度为200 μm 的316L 不锈钢衬底进行稳态导热换热，其余边界均允许对流散热。衬底底部、预热以及环境温度均设置为680 K。图6所示为316L不锈钢粉末选区熔化过程的典型微观结构演化，其中可直接观察到熔池中的熔体流动。由于存在重力作用，在凸面处的熔体会向下流动，引发表面和气孔附近的平展流。此外，在冷却时熔体会发生凝固，其凝固前端和晶粒生长方向沿着局部冷却方向，即温度的负梯度方向。固液相变由Allen-Cahn动力学方程控制，其随时空逐渐演化，并非在温度超过熔点后立即全部瞬间熔化或凝固，因此，在相场模拟结果中，仍可观察到颗粒局部熔化的现象，而在凝固区域仍可观察到过冷熔体的存在。当凝固速率接近热束扫描速度时，熔池中形成了一个拖曳尾迹，在此尾迹后面可观察到柱状晶粒。熔体中的气泡若无法在表面释放出去，将在凝固的实体中形成气孔/空隙。在熔池外面，温度依然很高，足以使颗粒之间发生如3.2 和3.3 中的烧结现象，即相邻颗粒间形成颈缩相邻颗粒间形成缩颈。局部相变/形貌改变与温度场之间的相互影响，亦十分明显，比如熔体流动可使表面平整，并增大熔池面积。熔体流动在传质的同时也传递能量，故其可影响局部温度的分布。类似地，熔体凝固也不仅仅是沿着负温度梯度方向，还能形成与热束扫描前更为致密的结构，导致熔池前端和后端不同的传热环境，使得熔池后端更有利于导热，进一步造成熔池前端的温度梯度高于后端的温度梯度。

图6(b)和(c)所示为不同热束参数下熔池的几何尺寸。可以发现：当热束扫描速度相等时，熔池的长度和深度皆随着热束功率的增大而增大(v=2 000 mm/s，P=300～600 W)，如图6(b1)～(b3)所示；而在相等的热束功率P=400 W下(图6(c1)～(c3))，当扫描速度v从3 000 mm/s降至1 250 mm/s时，熔池的长度先增大，而当v降至足够低时，熔池的长度又会减小，原因可能在于已熔合区域形成连续致密实体，有利于导热，使热量更多地从已熔合区域释放，局部集中加热效应变弱，熔池长度反而减小，如图6(c3)所示。

图7所示为选区熔化微结构与热束功率P和扫描速度v的关系。由图7(a)可以看出，致密度等值线并不沿着直线P/v方向延伸，表明热束的比能量P/v并不能完全精确预测微结构特征。但对图7(a)的数据进行近似处理，可以发现：当P和v满足P-0.25v-100＞0时，选区熔化可获得大于90%的致密度。图7(b)所示为选区熔化生成的几种典型的微结构；图7(b1)和(b2)所示为倾斜柱状晶粒，并伴有少量气孔；图7(b3)～(b5)所示为柱状晶粒，但存在大量不规则气孔；从图7(b6)可见选区未发生大面积熔化，熔池间断；从图7(b7)可见选区无熔化。本文非等温相场模拟得到的倾斜柱状晶粒和无规则气孔等微结构特征，与实验结果相对吻合，如图7(c)～(e)所示。

图6 316L不锈钢粉末选区熔化的的相场模拟Fig.6 Phase-field simulation of selective melting of 316L stainless steel powder bed

4 结论

1)建立了粉末增材制造的热-熔体-微结构耦合的非等温相场模型，该模型全面考虑了温度梯度的复杂影响，并可通过热源项的设计，实现对基于不同高能集中热束(激光、电子束或电弧等)的粉末增材制造的模拟。

2)选区烧结粉末增材制造的非等温相场模拟，揭示了激光功率P和扫描速度v对表面形貌、温度分布、晶粒几何形状以及致密度等微观结构特征的影响规律，且发现当P-0.15v-23＞0 时，选区激光烧结316L 不锈钢粉床所形成实体的致密度大于90%。

3)选区熔化粉末增材制造的非等温相场模拟，揭示了气孔、熔池、晶粒取向、晶粒形状等微观结构信息与热束扫描参数之间的关联，且发现当P-0.25v-100＞0时，选区激光熔化316L不锈钢粉床所形成实体的致密度大于90%。

4)下一步工作中，将对熔池附近的物理现象进一步细分，考虑由于溶体急剧气化而造成的一系列效应，如反冲压力以及匙状小孔(Keyhole)的形成；并将从“微观结构-材料性能”关系入手，进一步考虑热历史所产生的残余应力对材料微结构演化及力学性能的影响。