组合初始缺陷对含裂纹加筋板极限强度的影响研究*

田兆哲 杨 平 胡 康 冯 帆

(武汉理工大学交通学院 武汉 430063)

0 引 言

船舶结构在建造和营运过程中，会产生各种缺陷，如焊接引起的初始缺陷、腐蚀、疲劳裂纹、撞击产生的凹痕等.缺陷的存在会影响船体结构的安全性和有效性.因此，对含缺陷船舶结构的极限强度进行评估具有重要意义.

施兴华等[1]研究了初始变形、焊接残余应力、凹痕等3种缺陷的单独或组合作用对完整加筋板极限强度的影响.Paik等[2]通过非线性有限元法分析了焊接残余应力对高强度钢船体板极限强度的影响规律.李政杰等[3]研究了残余应力对完整加筋板极限强度的影响.马丽等[4]分析了点蚀损伤对船体梁极限强度的影响.Xia等[5]考虑了船体板上初始缺陷和裂纹的组合作用，计算分析了其对船体板极限强度的作用规律.Cui等[6-7]利用有限元软件ANSYS对纵向压缩载荷下含裂纹船体板的剩余极限强度进行评估，分析不同长度、位置、倾斜角度的裂纹对极限强度的影响；又研究了受单轴压缩载荷作用的含裂纹加筋板结构的极限强度特性，分析了板厚、裂纹长度及裂纹分布对加筋板的极限强度、应力分布等方面的影响.

对船舶加筋板结构而言，在船体板和加强筋上均含有焊接产生的残余应力.同时，疲劳裂纹也最容易产生于板、筋相连处.目前对加筋板极限强度的研究已有大量成果，但绝大多数研究仅考虑了初始变形的影响，而对于焊接残余应力作用的研究仅限于无裂纹加筋板，对焊接初始缺陷和裂纹进行全面考虑和分析的工作还有不足.因此，研究焊接初始缺陷和疲劳裂纹的组合作用对加筋板结构极限强度的影响十分必要.本文通过非线性有限元法，对同时含初始缺陷和疲劳裂纹的加筋板极限强度进行综合计算分析，讨论不同程度的初始缺陷、不同长度和分布的裂纹对加筋板极限强度的影响规律.

1 有限元模型

1.1 加筋板几何特征及材料属性

加筋板模型选自ISSC2012极限强度委员会报告[8]中的标准算例，其加筋板取自某散货船底，模型范围为单弯单跨，含2根加强筋，加强筋截面为扁钢.加筋板采用理想弹塑性材料，屈服准则为von Mises屈服准则，不考虑应力强化的影响.具体参数见表1.

表1 加筋板的几何和材料参数

1.2 裂纹形式

文中考虑的裂纹均为穿透裂纹，不考虑在加载过程中裂纹的扩展或闭合现象.现有的许多研究已表明：裂纹的宽度对结构极限强度的影响较小；而在相同长度下，横向裂纹相对于纵向或斜向裂纹对极限强度的影响较大.因此，本文中考虑的裂纹均为横向裂纹，裂纹宽度均取为3 mm，且裂纹均只存在于板上.

多数情况下，裂纹容易产生于板与骨材的焊接相连处.文中考虑裂纹在横向上的4种分布形式：单边裂纹、双边裂纹、单筋处板上裂纹和双筋处板上裂纹(裂纹对称分布于筋的两侧)，裂纹均处于跨中.裂纹长度以板格宽度的比例表示.裂纹形式见图1.

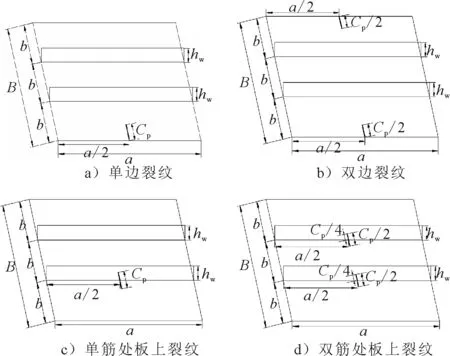
图1 裂纹分布形式

1.3 单元属性和网格划分

运用有限元软件ANSYS对加筋板模型进行数值分析，采用SHELL181单元建立板和加强筋的有限元模型.采用映射划分方式进行网格划分，将结构中远离裂纹区域的网格划分为边长25 mm的正方形；裂纹附近区域需进行网格细化，裂纹尖端建为半圆形，以防止裂纹扩展，裂纹尖端网格数目为16.

1.4 边界条件及加载

选取模型范围为单弯单跨，则加筋板四周都为横向、纵向强骨材所支撑.通常加筋板与强骨材交界处的约束介于简支和固支之间.一般而言，简支边界条件得到的计算结果较为保守，故本文采取四边简支的边界条件.同时，加筋板四周均应保持直边，还应约束加载边中点在y方向的位移和非加载边中点在x方向的位移，以限制刚体移动.

加筋板所受载荷为纵向压缩载荷，在有限元计算中采用位移控制法施加载荷，见图2.具体的加筋板边界条件如下.

加载边板的边界AA‴和BB‴：Ux=U′,Uz=0,θx=0,θz=0.

加载边筋的边界A′C′，A″C″，B′D′和B″D″：Ux=U′,Uy=0,θx=0.

非加载边板的边界AB和A‴B‴：Uz=0,Uy=Coupled,θy=0,θz=0.

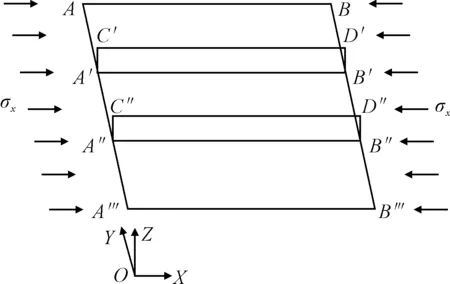
图2 加筋板边界约束

1.5 初始缺陷

初始缺陷包括初始变形和焊接残余应力.船体板的初始变形可采用瘦马形初始变形或板的屈曲模态模拟其形状，根据文献[8]，当纵向压力起主要作用时，采用瘦马形初始变形计算得到的极限强度偏大.因此，本文采用一阶屈曲模态模拟板的初始变形形状，以得到较为保守的结果.加筋板的整体初始变形为三种初始变形的叠加，分别为

式中：a和b为板格的长度和宽度；B为加筋板总宽度；A0，B0，C0分别为各种初始变形的幅值，板的初始变形幅值分为三种水平.

在船体构件的焊接相连部位，会产生拉伸残余应力.为保持结构内部应力平衡，在其他区域会产生压缩残余应力.对本文研究的加筋板而言，在板和筋相连处，板和筋上都会有残余拉应力；另外，在板的边缘也会有残余拉应力.在其他区域则会分布残余压应力.在数值模拟中，残余应力有四种理想化分布模型，本文中选取矩形分布形式.残余应力在板格上和加强筋上的分布见图3.

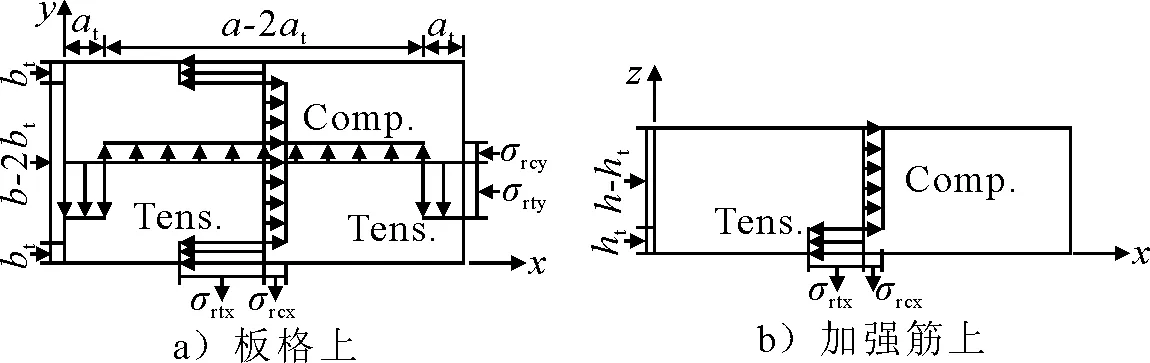
图3 残余应力分布示意图

根据应力平衡条件可得：

船体板上的纵向残余压应力也分为3种水平.

加强筋上的纵向残余压应力均为平均水平，即σrcx=-0.15σy.横向残余压应力与纵向残余压应力之间符合关系式.

式中：c为小于1.0的系数，当纵向应力起主要作用时，通常假定c为0.

文中考虑的载荷为纵向压力，不考虑横向残余应力的影响.文献[2]中指出，钢板中拉伸残余应力的幅值可恰好到达材料的屈服应力，而对于高强度钢材料，则需要做适当折减.板和加强筋上的纵向拉伸残余应力取为屈服应力的80%，即σrtx=0.8σy.残余应力以初始应力的形式施加于结构单元上，见图4.实际情况中，初始变形和残余应力可能会相互影响，本文为求简便，不考虑二者之间的影响作用.

图4 残余应力的施加

1.6 有限元方法的验证

选取文献[8]标准算例中的某散货船底双弯双跨范围内的加筋板结构，加强筋截面为扁钢，初始变形为平均水平.计算其在纵向压缩作用下的极限强度，结果见表2.由表2可知，本文的计算结果与文献[8]中较为吻合，证明本文极限强度计算方法的合理性.

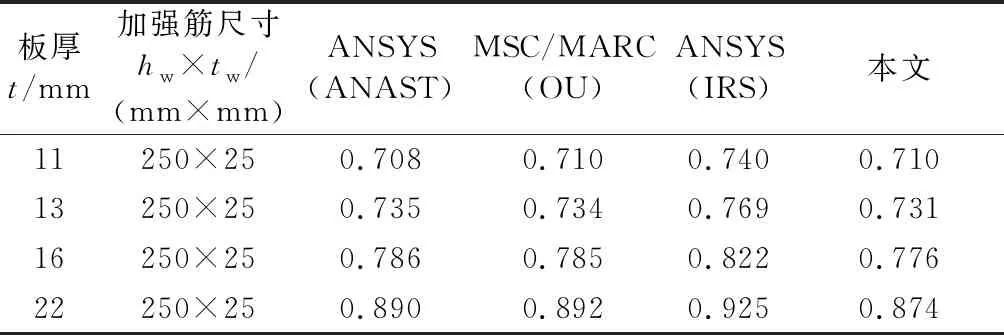
表2 双弯双跨加筋板极限强度(σu/σy)

Paik等[9]通过实验研究了轴向拉压作用对含裂纹板极限强度的影响，选取其中3个典型试件模型，计算其在无焊接残余应力和平均水平残余应力下的极限强度，见表3.由表3可知，考虑残余应力的影响后，有限元计算值均更为接近实验结果，误差也在可接受范围内，证明本文所采用的残余应力模拟方法的合理性.

表3 文献[9]中试件模型的极限强度 MPa

2 计算结果与分析

2.1 初始变形对极限强度的影响

对不同板厚、裂纹分布不同的加筋板极限强度进行计算，裂纹长度均为0.4b，考察不同水平的初始变形对极限强度的影响，不考虑残余应力的作用.计算结果见表4.

由表4可知，对于分析的所有含裂纹加筋板模型，其极限强度均随初始变形幅值的增加而减小.而随板的柔度降低，即板厚增加，加筋板的极限强度均会提高；但随着初始变形水平的提升，板厚较大的加筋板极限强度的降低幅度却明显高于板厚较小的加筋板.

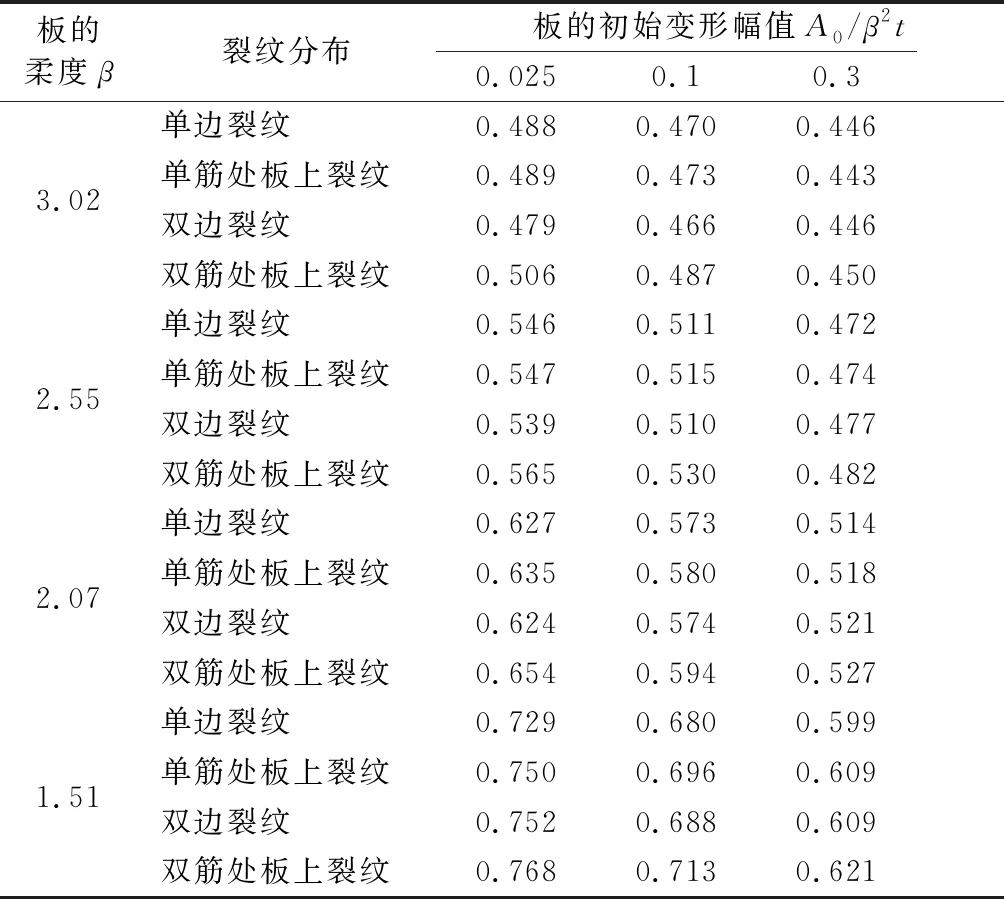
表4 初始变形不同水平下含裂纹加筋板的极限强度(σu/σy)

在裂纹的不同分布位置中，含双筋处板上裂纹的加筋板极限强度均较其他含裂纹加筋板更高，因此，双筋处板上裂纹对加筋板极限强度的影响较小.

当初始变形为轻微水平和平均水平时，含单筋处板上裂纹的加筋板极限强度略高于含单边裂纹、双边裂纹的加筋板；但初始变形为严重水平时，含单筋处板上裂纹的加筋板极限强度与含边裂纹的加筋板较为接近，有时甚至较低.可见，初始变形由平均水平升至严重水平时，含单筋处板上裂纹加筋板极限强度的降低幅度较大.

对于含边裂纹的加筋板，当初始变形为轻微水平时，含单边裂纹的加筋板极限强度高于含双边裂纹的加筋板，但板厚为22 mm时，含双边裂纹的加筋板极限强度较高；当初始变形为平均水平，板厚为11和13 mm时，含单边裂纹的加筋板极限强度较高；板厚为16和22 mm时，含双边裂纹的加筋板极限强度较高；初始变形为严重水平时，含双边裂纹的加筋板极限强度略高于含单边裂纹的加筋板.因此，相较于含单边裂纹的加筋板，含双边裂纹的加筋板极限强度因板厚增大而明显提升.

从平均应力-应变曲线上观察，以板厚13 mm、含单边裂纹和单筋处板上裂纹的加筋板为例(见图5)，随初始变形的水平增加，含裂纹加筋板的极限强度逐渐减小，刚度也会降低，但应力极值点对应的应变值却逐渐增大.

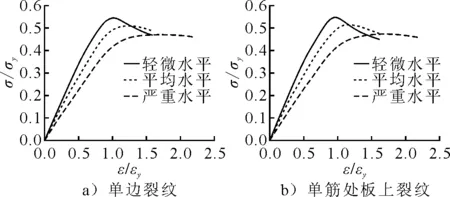
图5 初始变形不同水平下含裂纹加筋板平均应力-应变曲线

图6为板厚13 mm、含单边裂纹的加筋板处于极限状态时的应力云图.变形幅度上，初始变形的水平越高，加筋板在极限状态时的变形幅度越大.应力分布上，在裂纹附近均会产生应力集中现象，而低应力区均集中于有裂纹的板格上，高应力区处于远离裂纹的板格上.当初始变形的幅值逐渐增加，含裂纹的板格上的高应力区域逐渐扩大.

图6 初始变形不同水平下含单边裂纹的加筋板极限状态应力云图(板厚13 mm)

2.2 焊接残余应力对极限强度的影响

以板厚13 mm、裂纹长度均为0.4b的加筋板为分析对象，初始变形均取为平均水平，考察不同程度的焊接残余应力对其极限强度的影响.计算结果见表5，各加筋板应力-应变曲线见图7.

表5 残余应力不同水平下含裂纹加筋板的极限强度(σu/σy)

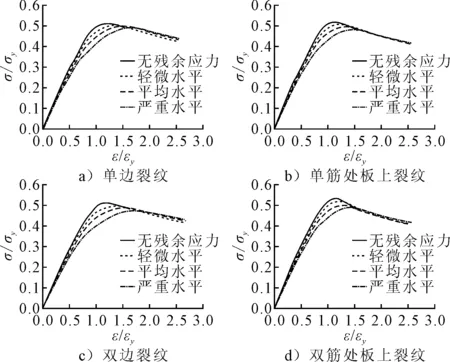
图7 残余应力不同水平下含裂纹加筋板平均应力-应变曲线

由计算结果和平均应力-应变曲线可知，对于4种裂纹分布的加筋板模型，极限强度均随残余应力的水平升高而降低.可见，残余应力对加筋板极限强度具有不利影响.同时，从各加筋板平均应力-应变曲线上可以看出，随残余应力的程度加大，应力极值点对应的应变值不断增大.

图8为不同残余应力水平下各加筋板极限强度的变化趋势，虽然极限强度值均有下降，但下降幅度却有较大差异.含双筋处板上裂纹的加筋板极限强度下降幅度最大，无残余应力时，其极限强度明显高于其他裂纹形式的加筋板；而当残余应力为平均水平和严重水平时，其极限强度已低于含单边裂纹的加筋板.含双边裂纹的加筋板极限强度的下降幅度略低于含双筋处板上裂纹的加筋板，含单边裂纹的加筋板极限强度降低幅度最小.

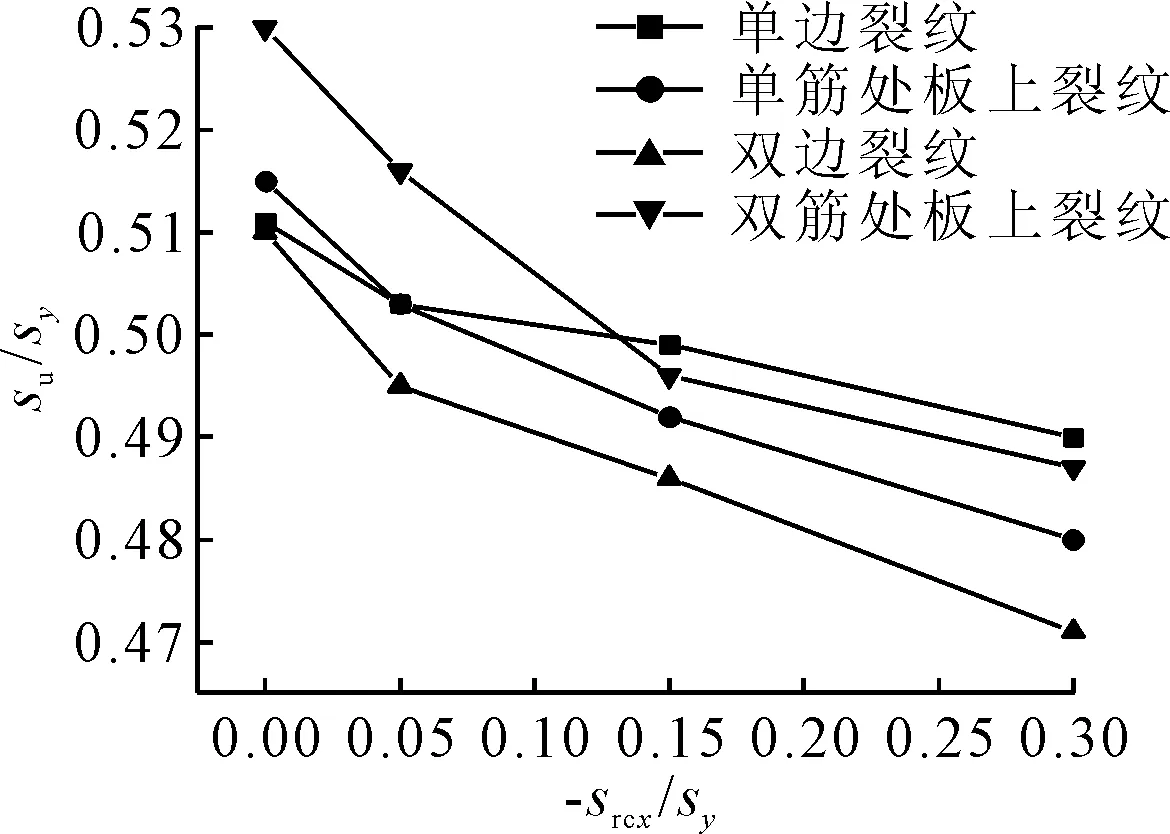
图8 残余应力不同水平下含裂纹加筋板极限强度变化趋势

出现这种现象的主要原因在于，在加筋板模型的边缘和板、筋相连处分布着拉伸残余应力，而裂纹同样处于这些位置.拉伸残余应力对于极限强度具有有利影响，压缩残余应力具有不利影响.因此，裂纹主要存在于拉伸残余应力的区域时，会削弱残余拉应力的有利影响.对于含双筋处板上裂纹和双边裂纹的加筋板，大部分长度的裂纹都处于残余拉应力区域内，对拉伸残余应力的有利影响的削弱作用更为明显，则含双筋处板上裂纹和双边裂纹的加筋板极限强度下降幅度更大.而对于含单边裂纹的加筋板，裂纹有很大一部分处于压缩残余应力区域中，削弱拉伸残余应力有利影响的同时，也抵消了部分压缩残余应力的不利影响，因此，极限强度的降低幅度较小.

以含双筋处板上裂纹的加筋板为例，其极限状态的应力云图见图9.应力分布上，随着残余应力水平的升高，加筋板的长边边缘和板、筋相连处的低应力区域逐渐扩大，这是因为拉伸残余应力的宽度在增大.而在裂纹附近，低应力区域相对于纵向上其他位置较小，高应力分布较多，表明裂纹附近较容易出现应力集中.

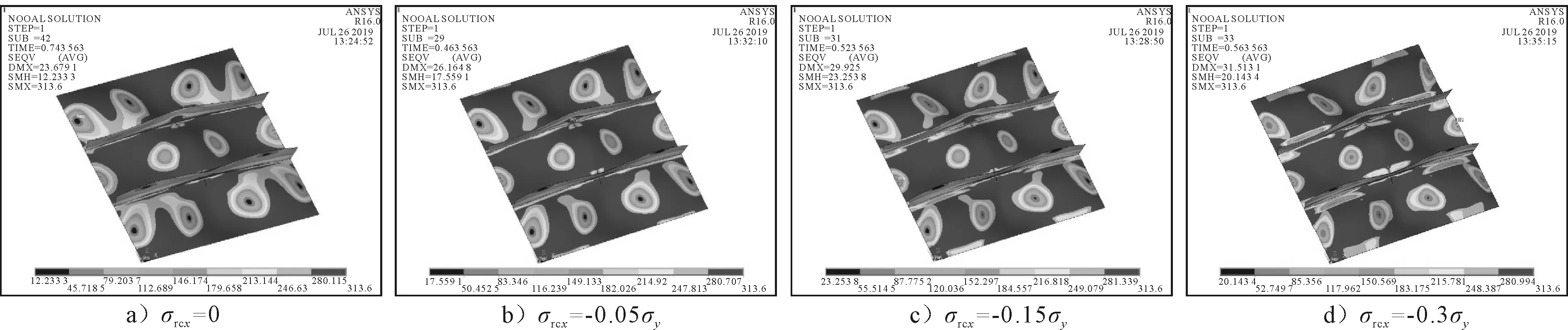
图9 残余应力不同水平下含双筋处板上裂纹的加筋板极限状态应力云图(板厚13 mm)

2.3 不同裂纹长度下残余应力对极限强度的影响

以板厚13 mm的含裂纹加筋板为研究对象，初始变形取为平均水平，残余应力取为严重水平，以突出其影响.考察裂纹长度不同时，残余应力对加筋板极限强度的影响，并与不含残余应力的情形相比较.残余应力为严重水平时，含不同长度裂纹的加筋板极限强度见表6，变化趋势见图10.

表6 残余应力严重水平下含不同长度裂纹的加筋板极限强度(σu/σy)

图10 不同裂纹长度下加筋板极限强度变化趋势(板厚13 mm，残余应力为严重水平)

由计算结果可知，尽管随着裂纹长度增加，含不同分布裂纹的加筋板极限强度均发生下降，但下降幅度截然不同.含单边裂纹的加筋板极限强度下降幅度最小，当裂纹长度为0.1b时，其极限强度在4种含裂纹加筋板模型中最小；而当裂纹长度为0.4b时，其极限强度最大.而含其他3种裂纹的加筋板极限强度下降幅度均较大.值得一提的是，随着裂纹长度的增加，含双筋处板上裂纹的加筋板极限强度下降速度明显加快，而含双边裂纹的加筋板极限强度下降速度却逐渐减弱.其主要原因在于，对于双边裂纹来说，裂纹长度从0.2b增至0.3b时，裂纹尖端从拉伸残余应力区域移至压缩残余应力区域内.因此，裂纹开始削弱压缩残余应力对极限强度的不利影响.而本文考虑的双筋处板上裂纹对称分布于加强筋的两侧，裂纹一直完全位于拉伸残余应力的区域内，裂纹长度的增长和对残余拉应力作用的削弱均对极限强度产生不利影响，加速了极限强度的下降.

将含严重水平残余应力的加筋板与不含残余应力的情形进行对比，4种加筋板极限强度的变化趋势见图11.整体而言，相对于不考虑残余应力时极限强度的降低幅度，只有含单边裂纹的加筋板在考虑残余应力时的极限强度下降幅度较小，其他3种含裂纹加筋板考虑残余应力时的极限强度下降幅度均较大.随着裂纹长度的增加，含单筋处板上裂纹和双边裂纹的加筋板考虑残余应力时的极限强度下降速度与不考虑残余应力时基本一致，说明裂纹较长时同时削弱了残余拉应力和残余压应力的影响.含单边裂纹的加筋板不考虑残余应力时，极限强度几乎为线性下降，考虑残余应力时，极限强度的降低速度随裂纹长度增加而明显减缓.这是因为单边裂纹长度为0.2b时，裂纹尖端已位于压缩残余应力区域内，之后裂纹的增长一直在削弱残余压应力对极限强度的不利影响.对于含双筋处板上裂纹的加筋板来说，却正好相反.如前所述，双筋处板上裂纹一直处于残余拉应力区域内，裂纹的长度增加本身已会导致极限强度降低，同时又减弱了残余拉应力对极限强度的有利影响，更加剧了极限强度的下降.因此，相对于不考虑残余应力的情形，含双筋处板上裂纹的加筋板考虑残余应力时的极限强度下降幅度随裂纹长度增加而不断增大.

图11 有无残余应力时各加筋板极限强度变化趋势

3 结 论

1) 船体板初始变形幅值的增加，会导致加筋板的极限强度下降，且板厚较大的加筋板极限强度下降幅度较大.双筋处板上裂纹对加筋板极限强度的影响最小，边裂纹对极限强度影响较大，含单筋处板上裂纹的加筋板极限强度随初始变形水平提高而下降的幅度最大.

2) 残余应力对加筋板极限强度具有不利影响，残余应力水平越高，加筋板极限强度越低.随着残余应力水平的提高，含双筋处板上裂纹的加筋板极限强度下降幅度最大，而含单边裂纹的加筋板极限强度降低幅度最小；同时，加筋板的长边边缘和板、筋相连处的低应力区会逐渐扩大.

3) 残余应力为严重水平时，随着裂纹长度的增加，含单边裂纹的加筋板极限强度下降幅度最小.相比于不考虑残余应力的情况，考虑残余应力时，含单边裂纹的加筋板极限强度下降幅度随裂纹长度增加而逐渐减小，而含双筋处板上裂纹的加筋板极限强度降低幅度随裂纹变长而逐渐增大.

本文仅通过数值计算，对一种典型加筋板结构(包括4种不同板厚)进行分析，研究不同水平的初始变形和焊接残余应力等初始缺陷的单独或组合作用对含裂纹加筋板极限强度的影响，得到上述主要结论.这些结论的普遍性、适用性和正确性尚需理论分析、模型实验等进一步研究工作的证实.