基于遗传算法的四缸双模天然气汽车加注时间优化
邓义斌 周 晴
(武汉理工大学能源与动力工程学院 武汉 430063)
0 引 言
近年来全世界天然气汽车产业发展迅猛的势头遭遇瓶颈,原因之一是供气体系不够完善、加气站建设滞后[1-2].针对加气站选址规划的优化[3]、站内燃料加注技术[4-6]等方面的研究一定程度改善这一局面,但仍无法从根本上解决加气站点数量不足的问题.为此人们开始探索如何拓展加气站点,例如,利用比加气站分布更为广泛的低压民用天然气管网作为气源进行燃料加注,通过Phill,FMQ2.5和FMQ10等设备实现从家用天然气管道取气进行压缩实现NGV的燃料加注, 但该类设备在安装要求、价格和加注效率之间此消彼长、不能兼顾.
双模天然气发动机技术[7]也是利用低压民用天然气管网作为气源进行燃料加注的一个典型代表,它是在不影响多缸发动机原有工作能力(即动力模式)的基础上,在停车时利用活塞式发动机与压缩机相似的特点,将一个或多个气缸切换为压缩气缸,而其余正常工作气缸为压缩气缸提供动力,实现从低压天然气气源的加压加注(即加注模式),该技术的优点在于不需要配备独立的压缩设备.Echter等[8]基于该技术开展6缸双模天然气发动机的改装、仿真计算、台架试验和实车应用等研究,通过对某型6缸5.9 L 12阀的柴油机进行改装及结构强化,采用三级压缩加注,从低压气源将140 L的天然气储罐加注至25 MPa约需要120 min,基于此情况提出双模天然气发动机的燃料加注效率仍有进一步优化空间.但当前天然气加注优化研究主要是利用现代智能优化算法对加气站压缩机的能耗和效率进行优化[9-10],对于双模天然气发动机这种较为特殊地燃料加注结构及方式并不适用.
文中针对4缸NGV发动机,运用双模技术对其进行改装设计,在假定改装后动力性满足要求的前提下,建立加注过程的数学模型并进行数值模拟,在此基础上建立以加注时间为优化目标的数学模型,并利用遗传算法求解优化问题.
1 双模NGV发动机改装设计
研究对象为某型NGV,其四缸CNG发动机的气缸行程为90 mm,缸径为83.5 mm,压缩比为10,车载储罐容积为60 L.双模NGV的CNG燃料加注需要有天然气气源、加压装置如压缩机等、动力和相应的管路及控制系统.利用NGV活塞式发动机与活塞式压缩机相似的特点,将四缸CNG发动机的一个气缸改装为压缩机,并为NGV增加相应的管路及控制系统,这样只需要将NGV接入民用管道天然气即可实现燃料自行加注.根据民用管道天然气压力(0.1 MPa)、车载储罐目标压力(20 MPa)、平均压力损失和最佳压力比可确定加注过程为四级压缩.其工作原理见图1,通过控制各级储罐的气体进出控制阀,可以实现管道天然气通过压缩气缸经过A、B、C三个中间储罐并最终到达车载储罐D.冷却器的作用是使压缩后的高温气体在进入各储罐前被充分冷却,提高加注效率.
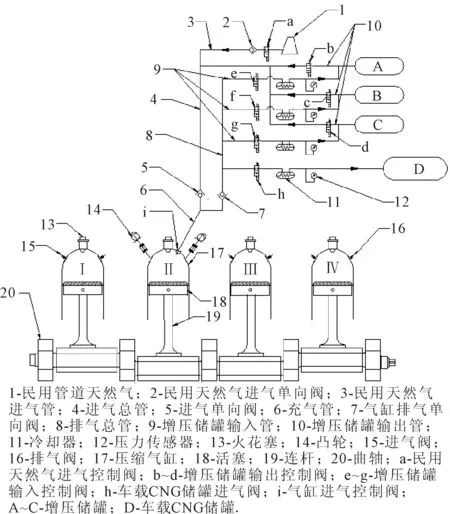
图1 双模NGV原理图
2 双模发动机加注过程建模计算
2.1 双模发动机加注过程建模及验证
根据能量守恒方程对气缸内热力学参数变化进行分析,对缸内气体内能产生影响的主要因素为流进和流出的气体携带的能量和活塞对气体做的功.
(1)
式中:dQ为在dθ曲轴转角内气缸内的吸收或释放的热量;dms,dmd为dθ曲轴转角内进入和流出的气体质量;hs,hd为dθ曲轴转角内进入和流出气缸气体的单位焓值;d(mcuc)为dθ曲轴转角内气缸内气体内能增量;dW为dθ曲轴转角内气体所作机械功的增量.
压缩气缸内的工作容积中,气体质量变化包括流入和流出气缸的质量,因此质量守恒方程为
(2)
式中:dm为缸内质量变化;dms,dmd分别为流入和流出气缸的流体质量.
根据式(1)、式(2)可得到压缩气缸模型,与气阀模型和储罐模型结合即可得到即可得出双模NGV加注工作过程气缸内气体和各级储罐内气体随曲轴转角的变化规律.
2.2 加注模型的验证
利用文献[11-12]的压缩机试验测试数据对所建的数学模型进行验证,试验p-V图见图2a),根据相关试验参数运用所建数学模型可得计算p-V图见图2b).由图2可知,膨胀和压缩过程的变化趋势基本一致,差异体现在进气和排气过程,与计算曲线较为平滑的进气和排气曲线相比,试验曲线呈现出较为明显的压力波动,主要原因是由于计算模型假设进排气时阀门瞬间打开,简化了气阀的实际运动造成的.总体而言,对比结果证实了压缩机工作过程数学模型合理可信,因此可以将该模型应用于双模NGV加注过程的数值计算.
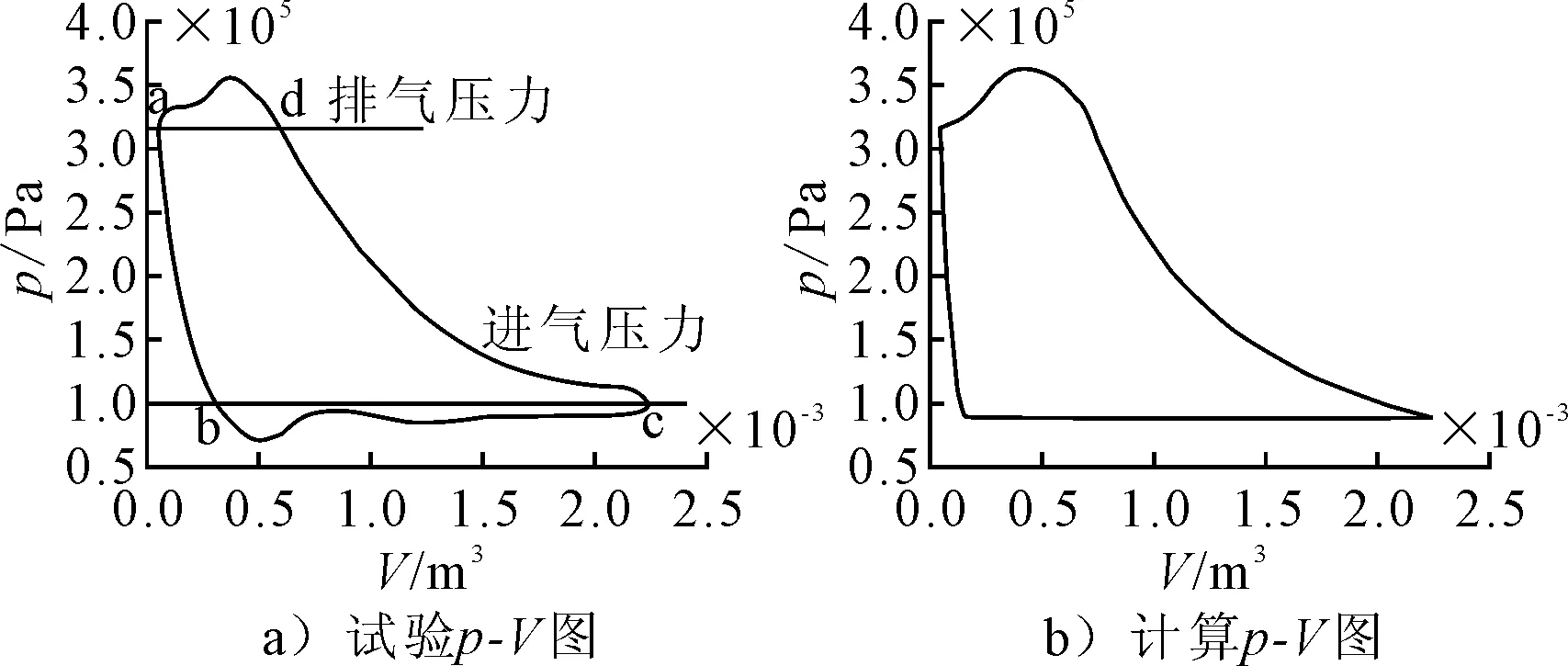
图2 压缩机试验与计算对比图
2.3 双模NGV加注工作过程计算与分析
假定压缩气体在进入储罐前被充分冷却至25 ℃,设定加注模式下发动机工作转速为1 000 r/min,考虑到空间限制,三个中间储罐容积均设为5 L,计算步长取0.1度曲轴转角,多级压缩过程中根据最省功原则和中间完全冷却原则采用等压比方法确定各级储罐的压力区间.
越级加注是从天然气气源(0.1 MPa)或低压力级别储罐依次向各个更高压力级别储罐进行加注,当作为气源的储罐压力低于设定下限时,将该储罐作为压力目标储罐,从低一级压力储罐为其加注直至车载储罐压力达到目标压力,加注过程各级储罐切换见表1,双模NGV车载储罐采用该方案对其加注.
整个加注过程所需压缩次数为48 467次,加注时间约为48.5 min.加注过程各级储罐气体压力变化见图3,各中间储罐内压力依次达到该压力上限然后在其压力区间内呈规律性震荡,直至车载储罐内压力呈阶梯状逐步上升达到目标压力(20 MPa).当储罐作为吸气气源时,储罐压力随压缩过程的进行而减少,当储罐作为排气目标储罐时,而储罐的压力随压缩过程的进行逐渐增大,不参与压缩过程的储罐压力维持不变.

表1 越级加注方案顺序列表

图3 越级加注各储罐压力变化图
3 燃料加注时间的优化
3.1 问题分析及优化模型的建立
双模发动机接入家用天然气气源对车载储罐进行加注时,在一定发动机转速下,加注时间跟压缩次数直接相关.考虑到进行越级加注方案时压缩气缸的位置状态只能在中间储罐内压力达到临界值(设定的上下限压力)时才能切换,各级储罐的上下限压力的大小会直接影响到加注时间.如一级储罐的上下限压力变化时,加注过程的加注时间变化见图4,图中显示一级储罐上限压力在0.35~0.45 MPa时和一级储罐下限压力在0.19~0.24 MPa时的加注时间变化规律,可以发现加注时间随上下限压力的上升逐渐降低.由此可见各级储罐内的上下限压力会对整个加注过程的加注时间造成较大的影响.

图4 加注时间与一级储罐上下限压力关系图
以加注时间为目标函数,加注过程的各级中间储罐压力上限x1,x2,x3和各级中间储罐压力下限x4,x5,x6作为优化变量.函数的优化模型为
min(t)=f(x1,x2,x3,x4,x5,x6)
(3)
模型的约束条件为
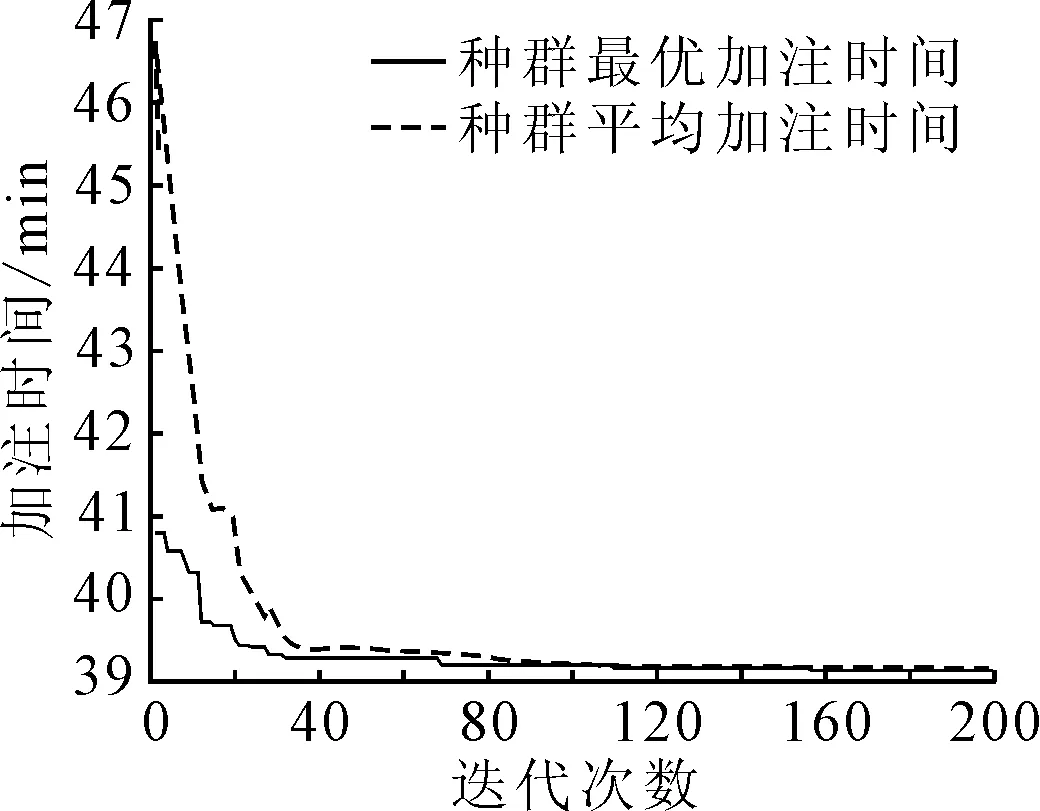
xi,l (4) 式中:i取1,2,3,4,5,6;xi,l为xi取值的下限;xi,h为xi取值的上限. 采用二进制编码对六个压力变量进行编码,采用锦标赛算子进行选择操作,对于交叉算子和变异算子均采用自适应操作.采用单点交叉进行交叉操作,并使用自适应的交叉概率,通过当前的适应值,确定交叉概率Pc的大小. (5) 采用基本位变异完成变异操作,并使用自适应的变异概率来进行变异操作. (6) 在计算过程中为防止当前种群的最优个体在下一代发生丢失,采用精英保留策略将当代最优适应值个体替换掉下一代种群中适应值最小的个体,组成新的种群.例: 第n代种群个体:p1,p2,p4,p5,p6,p7,…,p30 第n+1代种群个体:q1,q2,q4,q5,q6,q7,…,q30 种群个体均已按适应值从大到小排列,即p1为第n代最大适应值个体。在第n+1代时,q30为当前代最小适应值个体,根据精英保留策略,将该个体剔除,并用p1替代.则有: 第n+1代种群个体:q1,q2,q4,q5,q6,q7,…,q29,p1 遗传算法参数如下:种群大小为50,迭代次数为200,初始变异率为0.05,初始交叉率为0.8. 在一台六核主频2.4 GHz内存64G的工作站开展优化计算,约6 h完成计算.整个过程种群的平均加注时间和最优加注时间变化见图5.由图5可知,自适应遗传算法的收敛代数曲线比较平滑且速度较快,第40代时就收敛到较好的水平,且保证种群的平均加注时间与最优加注时间趋于一致.优化计算后的结果见图6,优化后的加注时间为39.1 min,优化后各级压缩压力区间见表2. 图5 遗传算法优化后加注时间变化曲线 图6 后加注过程各级储罐压力变化曲线 表2 优化结果对比表 MPa 由图6知,按照等压比原则得到的各级储罐压力区间计算得出的加注时间经过遗传算法优化后有较大幅度的减少. 运用双模技术对四缸NGV进行改装设计、开展燃料加注过程建模仿真工作,基于所建立的模型和计算条件,双模NGV从管道低压天然气实现储罐容积为60 L目标压力为20 MPa的燃料加注,加注时间约为48.5 min.针对双模NGV特殊的燃料加注方式,运用自适应遗传算法以加注时间为优化目标的优化模型进行求解,结果显示加注时间降低为39.1 min,降幅为19.4%.该算法设计合理,收敛速度较快,可为类似问题的优化提供参考.另外,遗传算法的算法复杂度较高,难以在实际行车电脑中应用,因此更简单高效的优化算法仍需探索.3.2 遗传算法设计
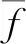
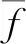
3.3 计算结果分析


4 结 束 语

