基于参数自跟踪的沥青路面使用性能预测研究*

杨 博 侯明业 毛海臻 王笑风

(河南省交通规划设计研究院股份有限公司 郑州 450000)

0 引 言

沥青路面由于其施工周期短、养护维修方便、行车舒适性高等优点，在高速公路建设过程中得到广泛应用.但受自然环境和行车荷载影响，沥青路面使用性能逐年下降，严重影响道路行车安全.通过对路面使用性能进行预测，掌握路面使用性能的发展趋势，进而确定路面的最佳养护时机，可有效保证沥青路面行车舒适性、安全性及运输经济性[1-3].

近年来，国内外学者相继提出了确定型、概率型等多种形式的网络预测模型[4-6]，但均存在计算过程繁琐、对原始检测数据样本数量和质量要求较高等问题.沥青路面使用性能数据具有典型的时序性、非线性等特点，且时间序列样本数量较少，数据集合常常无法满足传统模型学习需求，导致预测结果精度较低[7-9].

文中针对现有预测模型局限性及路面使用性能数据特征，建立了基于参数自跟踪的路面使用性能预测模型，研究了参数物理意义及对预测方程的影响规律，提出了模型参数修正方法，并采用不同路面使用性能评价指标进行预测分析，验证了参数自跟踪方法在路面使用性能预测领域应用的可行性.

1 预测模型建模

1.1 预测模型

路面使用性能预测模型在路面投入使用初期各项评价指标应处于最大值，预测指标在路面养护工程未介入情况下随着运营时间增加逐渐减小，且预测模型变化趋势最大程度贴切路面使用性能衰减规律.根据上述基本条件并结合路面使用性能衰变规律，综合国内外研究成果,运用余弦函数进行大量数据拟合，建立了路面使用性能预测方程，为

(1)

式中：I为路面使用性能评价指标预测值；I0为路面使用性能评价指标初始值；t为路面运营年限；α和β为方程参数.

1.2 参数分析

预测方程中的未知参数主要为α和β，为进一步分析两参数的物理意义及对预测方程的影响规律，选取不同参数值进行回归分析，具体结果见图1.

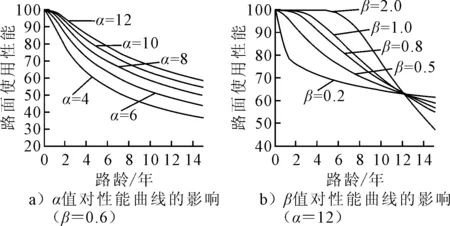
图1 不同参数值对性能曲线的影响

由图1可知：

1) 在β参数值固定的情况下，随着α值的增加预测线形的变化趋势较小，表明参数α对线形的影响较小，且由式(1)可知，当t=α时，I总是通过0.77I0，因此将α参数定义为使用寿命因子.

2) 在α参数值固定的情况下，当β参数值为0.2和0.5时，预测曲线形式为凹型，路面使用性能呈现早期衰减较快、后期平缓趋势.随着β参数值得增加，预测线形由凹曲线转变为凸曲线，不同的β参数值决定了预测曲线线形，因此将参数β定义为线形因子.

3) 参数β对线形的影响程度明显大于参数α，且唯一固定的参数α和参数β可确定路面使用性能衰变曲线.

1.3 参数修正

1)α值修正 使用寿命因子α在筑路材料、结构设计、施工质量,以及运营养护水平等多种因素影响下动态变化，参考文献[10]建立使用寿命因子求解方法，为

α=ka1hb1Lc1[1-exp(-(a2hb2Lc2/l0)a3hb3Lc3)]

(2)

式中：h为沥青层厚度，cm；l0为设计弯沉，0.01 mm；a1，a2，a3，b1，b2，b3，c1，c2，c3为回归指数，取值见表1.

表1 标准轴载下参数取值

2)β值修正 由于参数β对线形的影响程度较大，采用参数自跟踪方法进行测算，结合历年路面使用性能实测评价指标值(I1,I2,…,In)，计算出mn，再进行反算得出前n年各年实际的参数β1,β2,…,βn，进而预测第n+1的参数βn+1，路面进行专项养护或修复工程后重新反算参数β，为

βn+1=kn+1βn+kn+1mn+1βn-1+…+

(3)

mn=βn/βn-1

(4)

由式(3)～(4)可知，距离预测年份越远的路面使用性能检测数据对预测指标值的影响越小，年份相距较近的数据对预测值的影响程度较大，预测参数β对近期检测数据的依赖程度更高.

为进一步验证预测模型的预测精度，设预测方程I=f(t,β,α)，由于未知参数α,β相互独立，暂且认定α为常数，则预测方程为

I=f(t,β)

(5)

Ii=f(ti,β)+μi

(6)

式中：ti，Ii为第i次观测的自变量和因变量值；μi为预测模型误差.

设n+1年形状因子的预测值为β，则有：Ii-In+1=f(ti,βi)-f(tn+1,β).

由于I=f(t,β)关于参数β连续可导(其中β为自变量，t为常数)，根据拉格朗日中值定理，必定至少存在一个β′∈(βi,β)使得：

f(ti,βi)-f(tn+1,β)=f′(t,β′)(βi-β)

[f(ti,βi)-f(tn+1,β)]2=[f′(t,β′)(βi-β)]2

令：max[f′(t,β′)]2=L

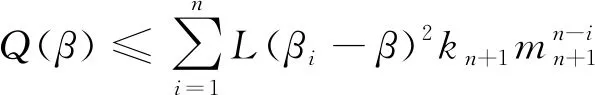
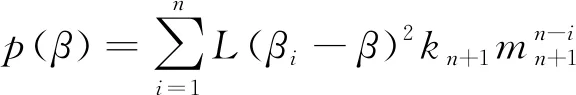
要使p(β)最小，即dp(β)/dβ=0

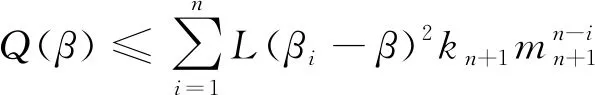
2 应用实例

2.1 数据来源

数据信息来源于京港澳高速，选取2009—2017年路面关键性评价指标PCI和SRI检测数据进行预测分析，具体检测数据及该路段历年的标准轴载作用次数见表2～4.

表2 京港澳高速PCI实测值

表3 京港澳高速SRI实测值

表4 京港澳高速标准轴载作用次数

2.2 预测结果分析

根据京港澳高速路面使用性能检测指标实测值以及历年标准轴载作用次数，利用预测模型对京港澳高速路面使用性能进行预测，预测结果见表5和图2.

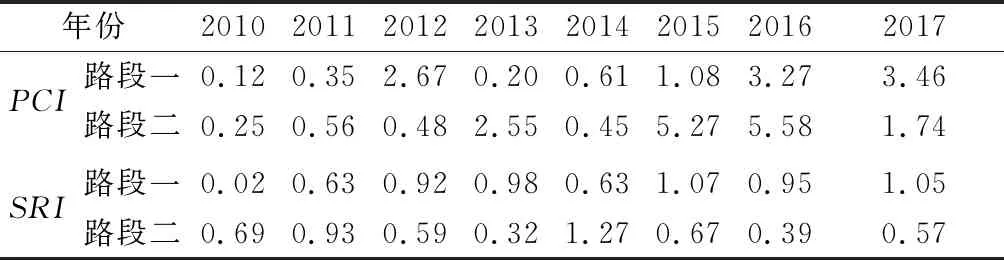
表5 预测结果RE %

图2 路段一、二的PCI和SRI预测结果

引入相对误差RE来衡量参数自跟踪模型对预测结果准确性的影响，为

(7)

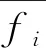
由表5可知：

1)PCI和SRI两项指标的初始预测精度较高，主要是预测初期路面技术状况较好，日常性养护对指标影响程度较低，路面使用性能评价指标实测值衰减曲线较为稳定，则路面使用性能评价指标预测值也较为稳定，相对误差较小；PCI指标由于后期专项养护工程介入导致指标波动较大，预测精度有所下降[11-12].

2) 参数自跟踪预测方法PCI，SRI预测结果的最大相对误差分别控制在5.58%和1.27%范围内，整体误差处于较低水平，基于参数自跟踪的路面使用性能预测模型精度较高，预测曲线与实测曲线较为吻合，可准确反映路面各项性能的衰变发展情况.

3 结 论

1) 结合路面使用性能衰变规律，建立了基于参数自跟踪的路面使用性能预测模型，系统研究了参数物理意义以及对预测方程的影响规律，结果表明参数β对线形的影响程度明显大于参数α，且唯一固定的参数α和参数β可确定路面使用性能衰变曲线.

2) 根据道路标准轴载发展规律，提出了参数α的修正方法，同时以最小二乘法为理论基础，通过路面使用性能评价指标实测值不断动态调整参数β，提升模型预测精度.

3) 以京港澳高速检测数据为例，对PCI，SRI等指标进行预测，发现基于参数自跟踪的路面使用性能预测模型曲线与实测值的契合程度较高，相对误差控制在5.58%范围内，验证了参数自跟踪方法在路面使用性能预测领域应用的可行性.