山区公路弯道小型车辆的比功率分布特征研究*

黄颖铭 刘丹丹 陈金山 郭建钢 李 林

(福建农林大学交通与土木工程学院 福州 350002)

0 引 言

机动车比功率(vehicle specific power,VSP)指的是单位质量下机动车的瞬时功率，单位为kW/t，由Palacios等首次提出[1].相较于其他的机动车行驶参数而言，VSP更容易获取且接近实际情况.许多专家学者对此做出了大量研究，已采用VSP来刻画机动车的运行状态和能耗测算的影响[2-3].美国环保署EPA发布了基于VSP的油耗排放计算模型MOVES2014，利用VSP来描述车辆不同运行工况，从而建立宏观交通参数与微观油耗之间的关系[4-5]；Zang等[6]提出一种基于机动车比功率分布的生态驾驶行为评价方法，表明个体驾驶员的VSP分布与基本分布的差异可用来识别生态驾驶行为，并在不同的车速范围内，其生态驾驶行为一致；王敏等[7]着重研究介于低速与高速两者之间的VSP分布，表明高速区间下VSP分布接近于正态分布；雒文鹏[8]提出车型混合比的概念，建立高速公路混合交通流比功率及比功模型；冯红晶[9]对商用车的VSP参数进行标定，得出不同轴型货车及客车的VSP计算模型.

美国环保署EPA与国内外研究学者们对不同车型、不同速度区间和不同道路等级下比功率的相关研究十分成熟，但对弯道、信号控制交叉口、公交车站等特殊路段的研究较少.为此，选取福州市森林公园至鼓岭道路的6个弯道作为研究对象，采用无人机实地航空摄影，利用Tracker软件获取车辆行驶数据，聚类分析小型车弯道处不同平均行程速度区间下的VSP分布特征，量化VSP在弯道处的变化趋势，拟合小型车VSP、平均行程速度和断面位置的三维关系，有助于更好地理解山区弯道VSP的分布特征.

1 研究方法

1.1 研究对象

以福州市森林公园经宦溪至鼓岭景区道路的6 个弯道为研究对象.限于篇幅，选取其中一个弯道(K17+477.003)说明，其几何参数从竣工图获取，见表1.该路段为典型的山区道路，双向两车道，设计速度为20 km/h，根据实地调查，交通流主要为小型车辆.

表1 弯道(K17+477.003)参数信息

1.2 VSP数据获取

为获取小型车自然行驶状态下的参数，采用无人机进行航空摄影，获得1 080 P,25帧/s的超高清视频.选择旅游淡季进行调查，以降低车辆跟驰行驶和对向车辆所造成的影响，摄像时段为09:00—11:00.

使用Tracker软件对过弯车辆进行自动跟踪，将视频导入并设置视频播放帧数为15帧，即0.6 s读取1次数据[10].定义弯道起点为坐标原点，利用质点跟踪功能，选取车辆的一个固定特征点进行跟踪，获取自然行驶车辆的速度、加速度和断面位置.将弯道外侧的行车方向定义上行，弯道内侧的行车方向定义为下行.根据统计学最小样本量的要求(上下行各为61辆)，因此采集了上下行样本量各70辆[11].

1) 速度计算 通过Tracker软件得到间隔15帧，3个固定特征点的坐标，记为(x1，y1)，(x2,，y2)，(x3，y3)，则速度v1，v2的计算为

(1)

(2)

2) 加速度计算 加速度a的计算为

a=(v2-v1)/Δt

(3)

3)VSP计算 由于小型车的各种相关参数取值范围较小，故而公式较为统一，VSP为

VSP=v[1.1a+9.81grand(%)+0.132]+

0.000 302v3

(4)

式中：v为瞬时速度，m/s；a为加速度，m/s2；grand为道路坡度，%.

1.3 VSP聚类分析

为了便于分析，对弯道处所得的VSP进行聚类[12].对通过弯道的每一辆车辆的瞬时速度求取平均，得到车辆过弯的平均行程速度，波动范围在20～50 km/h，以10 km/h的行驶速度对机动车平均行程速度进行区间划分，上行VSP的波动范围在-28～28 kW/t，下行VSP的波动范围在-16～20 kW/t，以2 kW/t的步长对不同速度区间下的VSP进行划分.VSP区间划分，见表2.

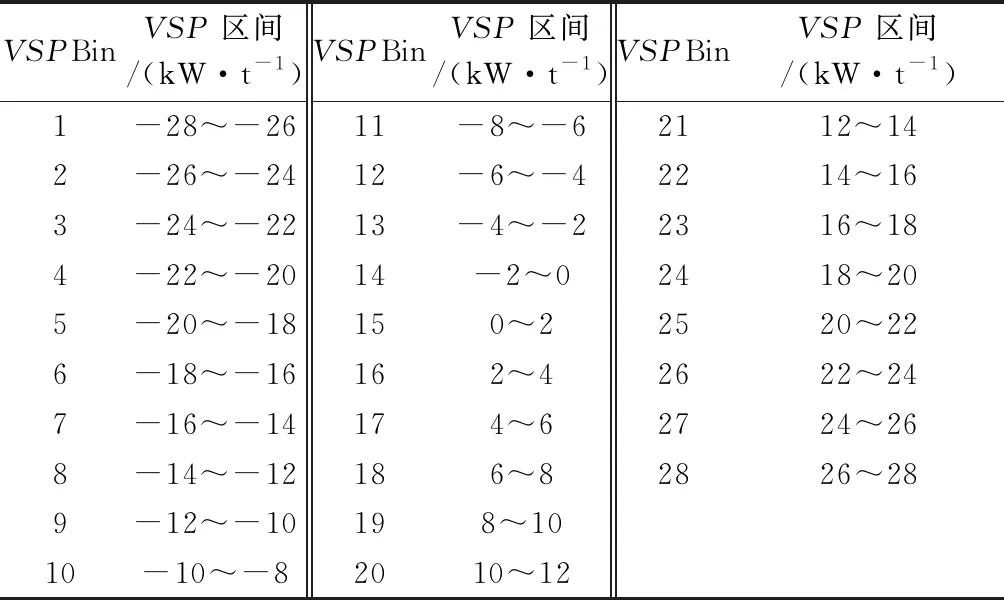
表2 VSP区间划分

2 结果与分析

2.1 VSP分布特性分析

VSP分布率为不同平均速度区间下VSP的个数占该VSP总数的比重.分上行和下行统计不同行程速度区间各VSP区间的分布率，见图1.

图1 上下行车辆在不同速度区间下的VSP分布图

从图1可以看出，车辆在上下行车辆在不同速度区间内的VSP分布特征.

1) 上下行车辆在不同平均行程速度区间下，其VSP分布均接近正态分布，在20～30 km/h的速度区间下，正态性最显著，且随着速度区间值的变小，VSP的波动范围变小，更加聚集分布在某一VSP区间范围内.

2) 在速度为40～50 km/h的区间下，VSP波动范围较大，上下行车辆的VSP均出现两个波峰，上行车辆的VSP主要分布在0～2 kW/t和14～16 kW/t，下行车辆的VSP主要分布在-2～0 kW/t和8～10 kW/t.

3) 速度为30～40 km/h的区间下，上行车辆的VSP主要分布在8～10 kW/t，下行车辆的VSP主要分布在-2～0 kW/t；在速度20～30 km/h的速度区间下，上行车辆的VSP主要分布在6～8 kW/t，下行车辆的VSP主要分布在0～2 kW/t.

2.2 不同断面位置VSP规律分析

上下行车辆各断面位置与相对应的VSP采用三次多项式拟合，可得该弯道上下行车辆VSP变化曲线图，见图2.

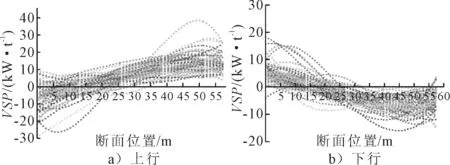
图2 上下行车辆-VSP变化曲线图

由图2可知，上行车辆在断面位置-VSP的变化曲线中，VSP大致趋势随着断面位置的增大而增大，VSP从负区间变为正区间，下行车辆的变化曲线刚好相反，VSP大致趋势随着断面位置的增大而减小，VSP从正区间变为负区间.

采用Getdata软件对车辆在该弯道上下行VSP的变化趋势进行量化，以5 m为单位对上下行车辆VSP变化曲线图取值，并求取平均，添加趋势线，可得上下行车辆平均VSP变化曲线图，见图3.

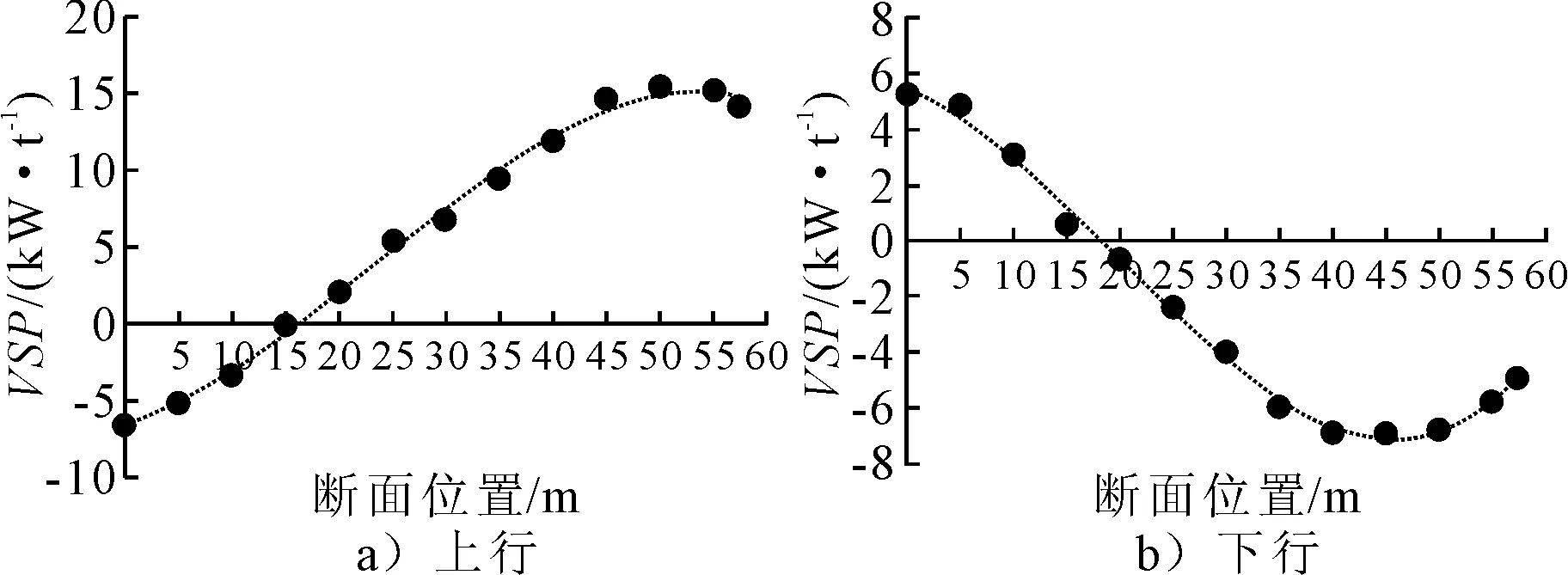
图3 上下行车辆VSP平均变化曲线图

对上下行车辆进行拟合，可得车辆VSP平均变化曲线函数，为

上行：y=-0.000 2x3+0.015x2+0.211 9x-

6.489，R2=0.996

(5)

下行：y=0.000 2x3-0.011x2-0.162 5x+

5.503，R2=0.996

(6)

式中：y为VSP，kW/t；x为断面位置，m.

由图3可知，上行车辆于断面位置约16.1 m处VSP由负转正，下行车辆约18.4 m处VSP由正转负，上下行零点的断面位置大致相当.可将曲线的变化原因归为，上行入弯时，先刹车减速，后由于车辆爬坡，VSP呈增长趋势，并于约16 m处，车辆开始加速；下行入弯时由于坡度、惯性，车辆下坡加速，后由于刹车制动，VSP呈下降趋势，并于约18 m处，车辆处于减速状态.

2.3 弯道VSP曲线拟合

使用matlab的curve fitting工具箱拟合平均行程速度、断面位置和VSP的关系，VSP与平均行程速度的关系满足一次多项式，VSP与断面位置的关系满足三次多项式，上下行关系拟合三维图，见图4.

上行车辆拟合的模型，为

f(x,v)=15.66-1.146x-0.598 5v+

0.022 98x2+0.040 61xv-0.000 155 6x3-

0.000 38x2v,R2=0.685 8

(7)

下行车辆拟合的模型为，为

f(x,v)=-9.286+0.694 4x+0.418 1v-

0.019 84x2-0.024 76xv+0.000 175 7x3+

0.000 278 7x2v,R2=0.612 3

(8)

式中：f(x,v)为VSP，kW/t；x为断面位置，m；v为速度，km/h.

由图4可知，可得到以下特征.

1) 随着小型车平均行程速度的增大，曲线所占的VSP分布区间越多，上下波动越剧烈.

2) 在断面位置为0时，上行方向速度越高，VSP相对越小，下行方向则相 反，速度越高，VSP相对越大；在断面位置为弯道终点时，上行方向速度越高，VSP相对越大；下行方向则相反，速度越高，VSP相对越小.

3 结 论

1) 上下行车辆在不同平均行程速度区间下的VSP分布均接近正态分布规律，速度越低，VSP的波动范围越小，更加集中分布于某一VSP分布区间，正态性越显著.

2) 上下行车辆的VSP平均变化曲线近乎相反，并在近似同一断面位置上VSP为零，车辆行驶工况发生变化.

3) 车辆过弯时，平均行程速度、断面和VSP间的关系满足多项式模型.上下行车辆平均行程速度越大，曲线所占的VSP分布区间就越多，上下波动越剧烈.

通过对山区公路弯道小型车辆的VSP分布特征进行研究，旨在对今后研究山区公路弯道小型车的油耗奠定基础，但仍存在问题需要进一步探讨：①研究其他坡度、半径的弯道和平均行程速度范围下的VSP分布特征；②在满足精度要求上收集更多车辆的相关数据，确保样本量充足，降低外界因素的影响；③将弯道的几何因素纳入考虑，进一步研究道路线形对VSP分布的影响.