KK型管节点应力集中系数几何敏感性分析

林海花，孙承猛，石 强

(1. 山东交通学院 船舶与港口工程学院，山东 威海 264200; 2. 大连船舶重工集团设计研究所有限公司，辽宁 大连 116005)

自升式平台能够在海上进行定点勘探开发作业，是当前海洋油气勘探开发装备中应用最为广泛的一种平台。随着平台作业水深的逐渐增加，以及对平台钻井能力要求的日益提升，当前设计建造的自升式平台大多采用质量轻但强度高的桁架式桩腿。

自升式平台依靠桩腿和桩靴站立于海底之上，外界环境载荷作用于海洋平台上，并传递至桩腿。因此，自升式平台桩腿[1]的强度安全关系到整座平台的安全性。一般地，对自升式平台桁架式桩腿的屈服强度和屈曲强度进行联合校核，通常桩腿与平台主体相连接的桩腿部位是综合应力最大的部位，而对桩腿的疲劳强度[2-4]则进行单独校核。由于处于波浪飞溅区的桩腿结构遭受波浪水质点椭圆运动产生的交变载荷作用，因而该区域的桩腿结构疲劳损伤[5]较大。同时，平台作业海域不固定，因而作业水深并不固定，再加上潮汐的变化，因此处于波浪飞溅区的桩腿部位是变化的。环境载荷的长期循环作用较为显著，使得桩腿疲劳研究分析成为自升式平台整体安全性分析的一项重要工作。

桩腿结构的疲劳损伤除了与外界的交变载荷有关外，还与结构的形式[6]有着极大的联系。结构几何不连续将引起结构的应力集中，这也是引起损伤的主要原因。自升式平台桁架式桩腿由高强钢钢管焊接而成，圆管构件相互交汇的节点称为焊接管节点，通过管节点将支管的载荷传递到弦杆上。在这些几何不连续的管节点处，应力状态较为复杂，会产生应力集中，对其热点应力的大小和位置的研究，是结构疲劳寿命评估中非常重要的工作。

学者对T型、Y型和K型[7-9]管节点应力集中和疲劳研究较多，但结构形式的稍微变化[10-11]都将对应力集中产生较大的影响。选取少有学者研究的自升式平台桁架式桩腿中采用的KK型管节点为研究对象，采用ANSYS软件进行参数化建模[12-13]，并对其热点应力进行分析，得到应力集中系数SCF，为自升式平台桩腿的疲劳分析和KK型管节点结构设计提供理论依据。

1 KK型管节点简介

所研究的KK型管节点包含两个完全相同的K型管节点，几何模型及相关尺寸定义如图1所示。

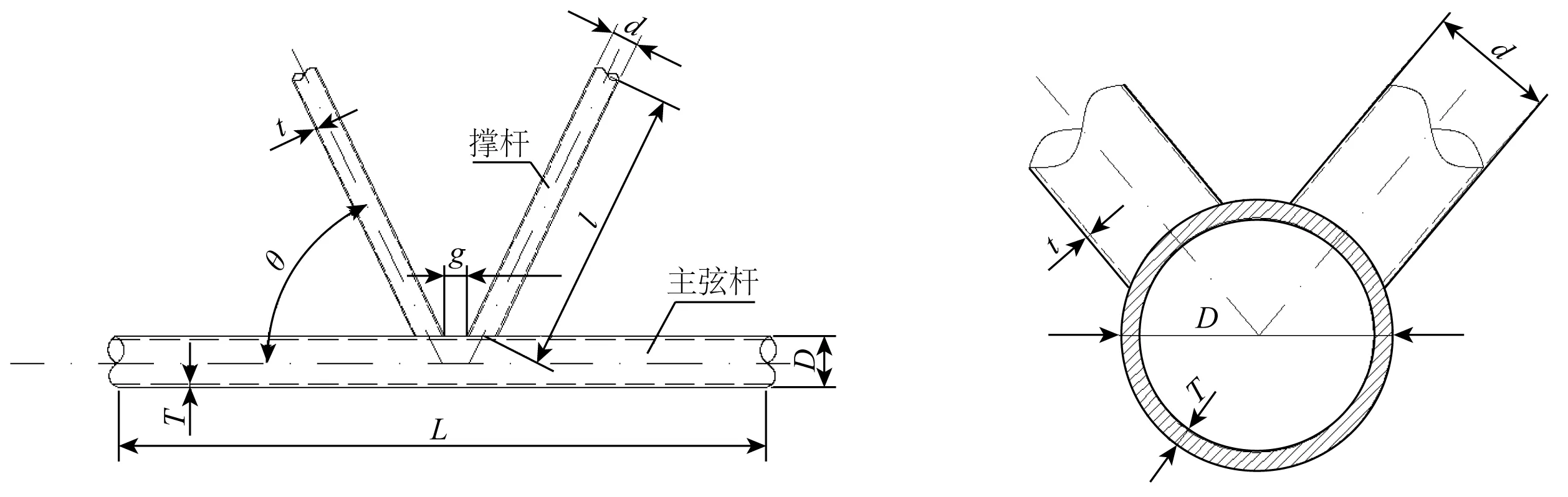
图1 KK型管节点的几何模型Fig. 1 Configuration of a KK tubular joint

可以看出，KK型管节点主要由一根弦杆和4根撑杆组成，各撑杆的直径和厚度相同，L为弦杆长度，D为弦杆外径，T为弦杆壁厚，d为撑杆外径，t为撑杆壁厚，θ为单K型一侧的弦杆与撑杆之间的夹角，g为单K型一侧两根撑杆在弦杆处的间隙。

管节点的几何参数还可通过无量纲参数来进行描述，具有相同无量纲参数的管节点可视为具有相同的力学性能。对比图1所示的KK型管节点几何模型，无量纲参数定义如下：

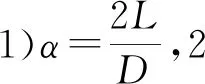
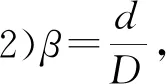
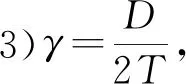
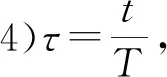
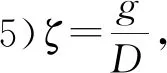
6)θ，弦杆轴线与撑杆轴线的交角θ，反映载荷的传递。

基于以上6个无量纲参数对KK型管节点应力集中系数SCF的几何敏感性进行研究分析。

2 参数化模型

对KK型管节点采取参数化建模[14]方式，以便于分析得到KK型管节点应力集中系数SCF对各几何参数的敏感性，为结构的疲劳分析和结构形式设计提供理论依据。根据前述无量纲参数的定义，在参数化建模中无量纲参数的取值范围如表1所示。

表1 KK型管节点无量纲几何参数取值范围Tab. 1 Dimensionless geometric parameters for KK tubular joints

选择带有厚度的壳单元创建分析模型，在某无量纲参数下，创建参数化模型如图2所示。

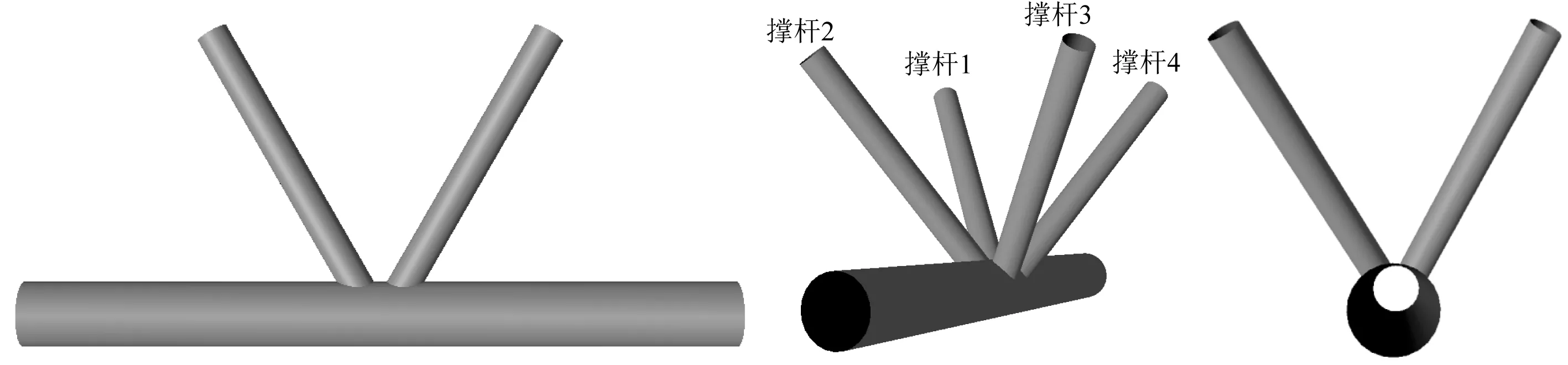
图2 KK型管节点的参数化几何模型Fig. 2 Parametric geometric model of KK tubular joints

划分网格时遵循以下原则：

1) 管节点附近即弦杆与撑杆相连接的区域应力和应力梯度均较高，采用与撑杆杆件厚度相同的精细网格尺寸进行划分，在杆件环向方向上网格沿着相贯线并包含冠点和鞍点，在杆件轴向方向上网格沿杆件的轴向(如图3所示)方向一层层地划分，保证至少有10层精细网格，并尽量使所划分网格呈正四边形，且避免出现扭曲畸形的网格；

2) 在远离弦杆与撑杆相连接处的区域采用稍微粗糙的网格进行划分，在保证分析精度的同时可以减少分析时间；

3) 在精细网格区域和粗糙网格区域之间划分网格时，应保证网格整体过渡协调合理。

根据以上原则，创建KK型管节点有限元分析的参数化模型，如图3和图4所示。

图3 KK型管节点热点附近的网格划分Fig. 3 Integral meshing diagram of KK tube joints near hot points

图4 KK型管节点的整体网格划分Fig. 4 Integral meshing diagram of KK tube joints

3 数值模拟方法

采用ANSYS软件对管节点疲劳性能进行有限元分析，计算应力集中系数SCF。

3.1 SCF的计算原理

应力集中系数SCF可通过热点应力和名义应力的比值[15]来获得。

热点是疲劳裂纹的起源点，热点应力[16-17]即为热点处的应力，与结构的整体焊接和受载有关。热点应力取焊接趾端处的最大局部应力，根据有限元数值计算结果，采用表面外推法求得。具体做法为：利用距离撑杆焊趾表面三个单元处的上、下表面的各单向应力分别进行二次插值计算，利用插值得到的结果再计算焊趾处的最大第一主应力，作为相应的热点应力。

自升式平台桁架式桩腿的撑杆同时承受着轴向力F、面内弯矩Mi和面外弯矩Mo的作用，假设撑杆受到独立的轴向力F或独立的面内弯矩Mi或独立的面外弯矩Mo的作用，则撑杆的各项名义应力计算公式为：

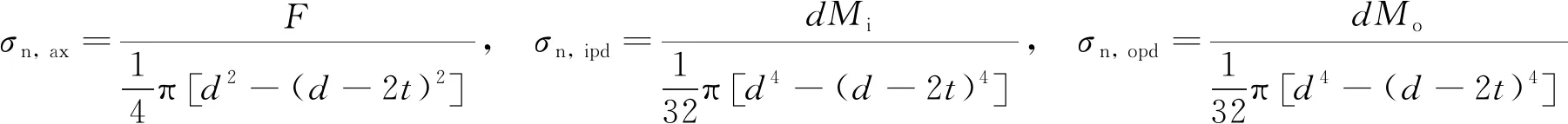
(1)

其中，σn, ax为由轴向力引起的名义应力；σn, ipd为由面内弯矩引起的名义应力；σn, opd为由面外弯矩引起的名义应力。

图5为一Y型管节点，其中，τ=0.03，β=0.467，γ=22.72，θ=60°，α=29.33。

以遭受面内弯矩为例，根据DNVGL[18]规范中的Efthymiou公式，可得撑杆相贯线冠点处的SCF为：

1+0.65βτ0.4γ(1.09-0.77β)(sinθ)(0.06γ-1.16)=1.709 8

图5 Y型管节点模型Fig. 5 Model of Y tube joint

(2)

创建Y型管节点有限元分析模型，在面内弯矩的作用下其应力云图如图6所示。

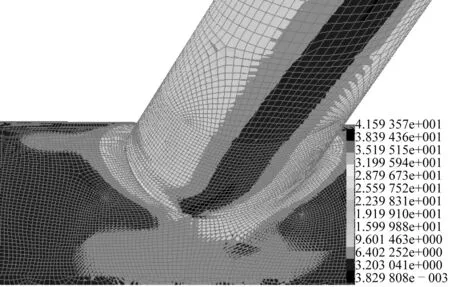
图6 面内弯矩作用下Y型管节点应力云图Fig. 6 Stress distribution of Y-joint under in-plane bending moment

由应力集中系数SCF等于热点应力和名义应力的比值，得该Y型管节点在面内弯矩作用下的撑杆冠点处的SCF为1.780 6，与Efthymiou公式的计算结果相近。因此，文中的分析方法合理，计算结果可靠。

3.2 边界条件

按照弦杆两端采用固定约束的方式取边界条件。

3.3 模型加载

由于SCF的大小与结构形式和载荷形式有关，而与载荷大小无关，因此参数化分析中，对每一种结构形式均采用如表2所示的加载方式。表中： ① 工况1～工况6分别为6种不同的载荷加载形式，载荷加载至KK型管节点的4根撑杆上； ② 工况1为撑杆分别承受轴向拉伸和轴向压缩的作用，工况2为撑杆均承受轴向拉伸的作用，其中，F为轴向拉力，-F为轴向压力； ③ 工况3和工况4为撑杆仅承受面外弯矩的作用，Mx为绕撑杆自身局部坐标系x轴(即沿着撑杆轴向)的弯矩，在撑杆局部坐标系中按照右手法则来确定弯矩的正负； ④ 工况5和工况6为撑杆仅承受面内弯矩的作用，My为绕撑杆自身局部坐标系y轴(即垂直于撑杆轴向)的弯矩，在撑杆局部坐标系中按照右手法则来确定弯矩的正负； ⑤ 应力集中系数SCF是应力的比值，与外载荷的数值大小无关，因此分析中统一取载荷值的大小为Mx=My=1 000 kN·mm，F=1 000 N。

表2 KK型管节点加载方式Tab. 2 Loading mode of KK tubular joints

4 数值仿真分析结果

采用参数化方式建模，建模时，根据表1设置α、β、γ、τ、ξ和θ的取值，首先固定其中任意5个无量纲参数，固定取值为：α=20，β=0.45，γ=18，τ=0.6，ξ=0.4，θ=45°，然后按照表1中给出的取值区间和取值间隔来依次改变另外一个参数。根据选取的参数和取值创建模型、进行数值分析，得到KK型管节点在各工况下的第一主应力，并分别计算各对应的名义应力，进而得到应力集中系数SCF。以下分别给出了不同工况、不同几何参数下撑杆焊接趾端处的最大SCF的分析结果。

4.1 KK型管节点SCF对α的敏感性分析

固定无量纲参数β、γ、τ、ξ和θ的值，改变α的值，KK型管节点SCF的分析结果如图7所示。

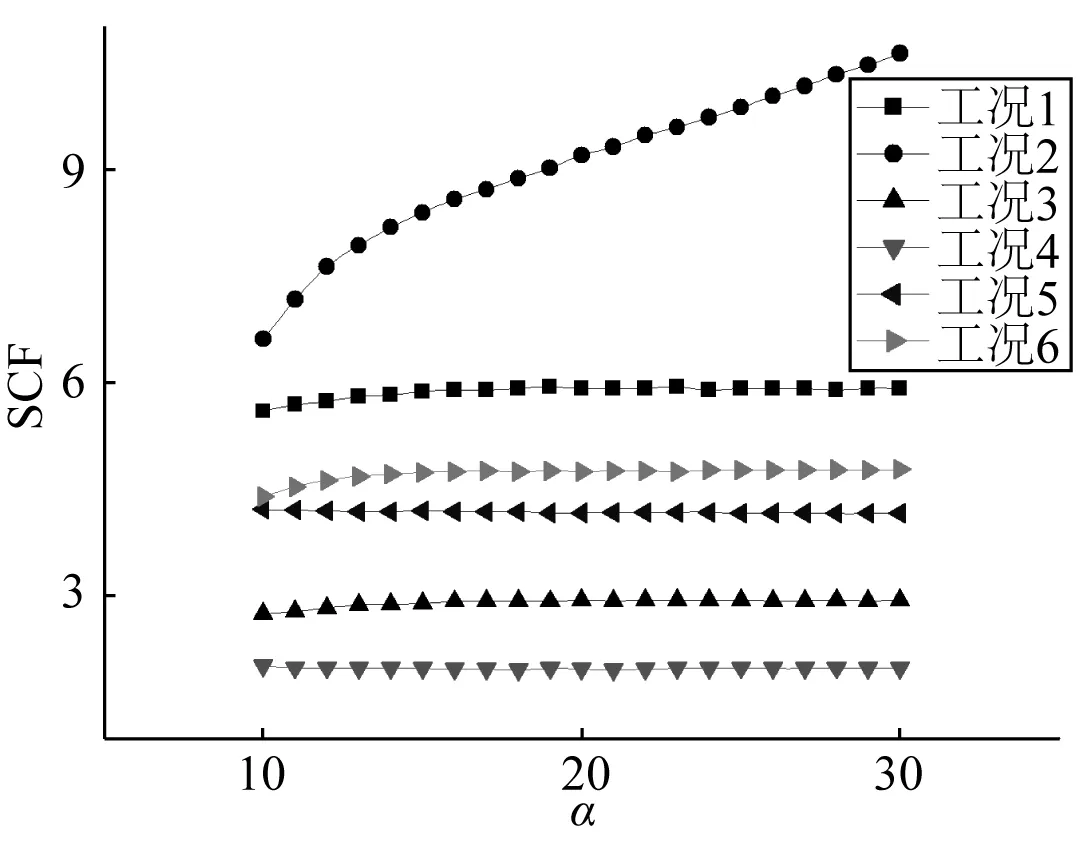
图7 KK型管节点SCF随α的变化Fig. 7 Variation of SCF with α of KK tubular joints

从图7可以看出，无量纲参数α对KK型管节点SCF的影响为：① 在工况2时，即撑杆均承受轴向拉伸的作用时，SCF随着α的增加而增加，在计算区域内SCF最大值为10.63，最小值为6.62，此时在满足其他性能要求时应考虑采用较小的α，即较大的弦杆直径; ② 在其他工况时，即撑杆分别承受轴向拉伸和轴向压缩的作用时或撑杆在弯矩载荷作用时，SCF随着α的增加基本保持不变，可见此时SCF与α基本无关; ③ 工况2下的SCF值较其他工况SCF值大; ④ 承受轴向载荷作用下的撑杆SCF值较承受弯矩载荷作用下的撑杆SCF值大; ⑤承受My时的撑杆SCF值较承受Mx时的撑杆SCF值大。

综合以上分析可知，在撑杆承受轴向拉伸作用时，增大弦杆直径或减小撑杆直径，从而减小无量纲参数α对减小KK型管节点SCF有利，在其他受力情况下α对SCF值的影响并不大。

4.2 KK型管节点SCF对β的敏感性分析

固定无量纲参数α、γ、τ、ξ和θ的值，改变β的值，KK型管节点SCF的分析结果如图8所示。

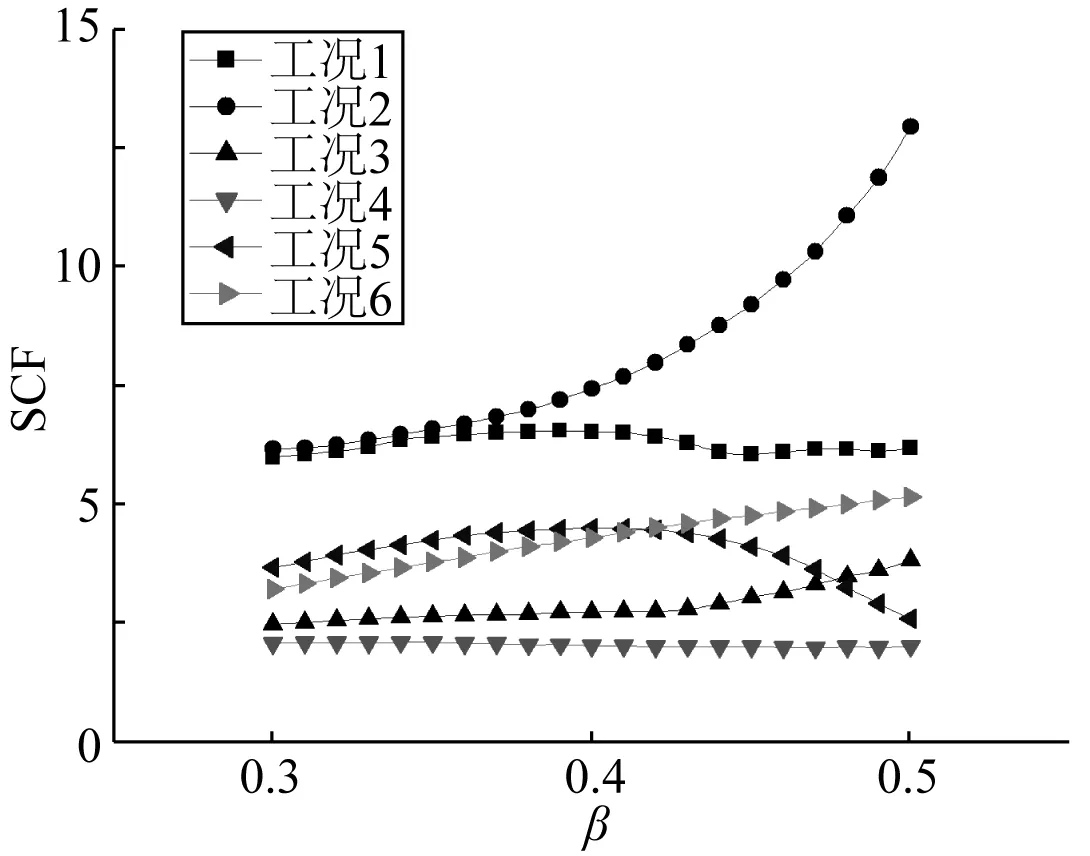
图8 KK型管节点SCF随β的变化Fig. 8 Variation of SCF with β of KK tubular joints

从图8可以看出，无量纲参数β对KK型管节点SCF的影响为：① 在工况2时，即撑杆均承受轴向拉伸的作用时，SCF随着β的增加而明显增加，尤其是当β超过0.4时，SCF增加速度较快。在计算区域内SCF最大值为12.93，最小值为6.15，增加了110.24%，此时在满足其他性能要求时应考虑采用较小的β，即采用较小的弦杆直径; ② 在工况6时，SCF随着β的增加而增加，但增加速度较工况2的增加速度缓慢，在计算区域内SCF最大值为5.13，最小值为3.20，增加了66.45%; ③ 在工况5即撑杆遭受正、负平面内弯矩共同作用时，SCF先随着β的增加而缓慢增加，从β为0.3时的3.65，增加到β为0.4时的最大值4.48，增加了22.74%，然后SCF随着β的增加而降低至2.57，降低了42.63%; ④ 在其他工况时，SCF随着β的增加基本保持不变，可近似地认为SCF与β无关; ⑤ 撑杆承受轴向载荷作用下的SCF值比承受弯矩载荷作用下的SCF值大，其中又以撑杆均承受轴向拉伸作用时的SCF值为最大; ⑥ 撑杆承受面内弯矩My作用时的SCF值较承受面外弯矩Mx作用时的SCF值大。

综合以上分析可知，KK型管节点的结构设计在满足其他要求以外，还应采用较小的β，尤其应避免β的值超过0.4，即取相对较大的弦杆外径或相对较小的撑杆外径对管节点的疲劳性能是有利的。

4.3 KK型管节点SCF对γ的敏感性分析

固定无量纲参数α、β、τ、ξ和θ的值，改变γ的值，KK型管节点SCF的分析结果如图9所示。

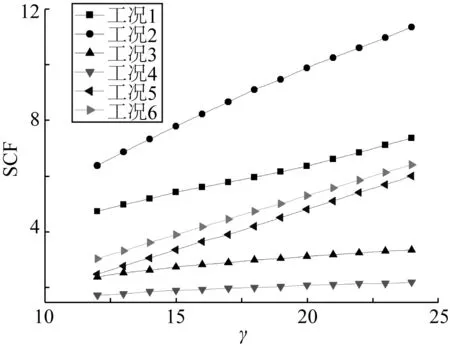
图9 KK型管节点SCF随γ的变化Fig. 9 Variation of SCF with γ of KK tubular joints

从图9可以看出，无量纲参数γ对KK型管节点SCF的影响为：① 在工况1、2、5和6时，SCF随着γ的增加而明显增加; ② 在工况3、4时，撑杆承受面外弯矩Mx的作用，此时SCF随着γ的增加基本保持不变，可近似地认为SCF与γ无关; ③ 在工况2时，即撑杆均承受轴向拉伸的作用时，在所有的γ计算值内，SCF值最大，在γ=24时达到最大值11.35，相比较于γ=12时的最小值6.39，增加了77.62%; ④ 撑杆承受轴向载荷作用下的SCF值较承受弯矩载荷作用下的SCF值大，其中又以撑杆均承受轴向拉伸的作用时的SCF值为最大; ⑤ 撑杆承受面内弯矩My作用时的SCF值较承受面外弯矩Mx作用时的SCF值大，且随着γ的增加，差值越来越大。

综合以上分析可知，KK型管节点的结构设计除了应该满足其他要求以外，还应采用较小的γ，即当弦杆的外径一定时，采用相对较厚的弦杆厚度对管节点的疲劳性能有利。

4.4 KK型管节点SCF对τ的敏感性分析

固定无量纲参数α、β、γ、ξ和θ，改变τ的值，KK型管节点SCF的分析结果如图10所示。

图10 KK型管节点SCF随τ的变化Fig. 10 Variation of SCF with τ of KK tubular joints

从图10可以看出，无量纲参数τ对KK型管节点SCF的影响为：① 在所有工况下，SCF均随着τ的增加而增加，故增大弦杆与撑杆厚度的差值可降低SCF; ② 在工况2时，即撑杆均承受轴向拉伸的作用时，在所有的τ计算值内，SCF值最大，在τ=0.95时达到最大值10.87，相比较于τ=0.25时的最小值4.26，增加了155.19%; ③ 撑杆承受轴向载荷作用下的SCF值较承受弯矩载荷作用下的SCF值大，其中又以撑杆均承受轴向拉伸作用时的SCF值为最大; ④ 撑杆承受面内弯矩My作用时的SCF值较承受面外弯矩Mx作用时的SCF值大，且随着τ的增加，差值越来越大。

综合以上分析可知，KK型管节点的结构设计除了应该满足其他要求以外，还应采用较小的τ，即当弦杆的壁厚一定时，采用相对较薄的撑杆厚度对管节点的疲劳性能是有利的。

4.5 KK型管节点SCF对ξ的敏感性分析

固定无量纲参数α、β、γ、τ和θ的值，改变ξ的值，KK型管节点SCF的分析结果如图11所示。

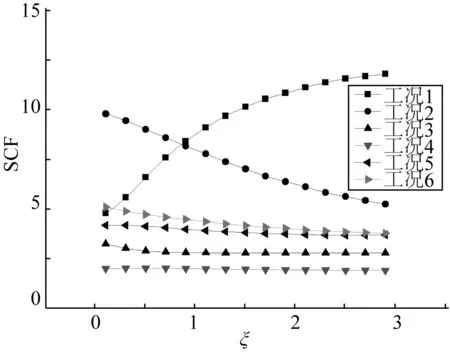
图11 KK型管节点SCF随ξ的变化Fig. 11 Variation of SCF with ξ of KK tubular joints

从图11可以看出，无量纲参数ξ对KK型管节点SCF的影响为：① 在工况1时，SCF随着ξ的增加而明显增加，由ξ为0.1时的4.78增加到ξ为2.9时的11.81，增加了约147.07%; ② 在工况2时，即撑杆均承受轴向拉伸作用时，SCF随着ξ的增加而明显减小，由ξ为0.1时的9.80减小到ξ为2.9时的5.24，减小了46.58%; ③ 结合工况1和工况2，应综合考虑轴向载荷的作用，取一个合适的ξ值，以达到理想的SCF; ④ 根据工况3～6的结果，可以看出当撑杆承受弯矩载荷时，ξ对SCF的影响不大; ⑤ 撑杆承受面内弯矩My作用时的SCF值较承受面外弯矩Mx作用时的SCF值大。

ξ与撑杆之间的间隙相关，故综合以上分析可知，KK型管节点撑杆之间的间隙取值，应综合考虑撑杆轴向载荷的作用以及生产施工等因素。

4.6 KK型管节点SCF对θ的敏感性分析

固定无量纲参数α、β、γ、τ和ξ的值，改变θ的值，KK型管节点SCF的分析结果如图12所示。

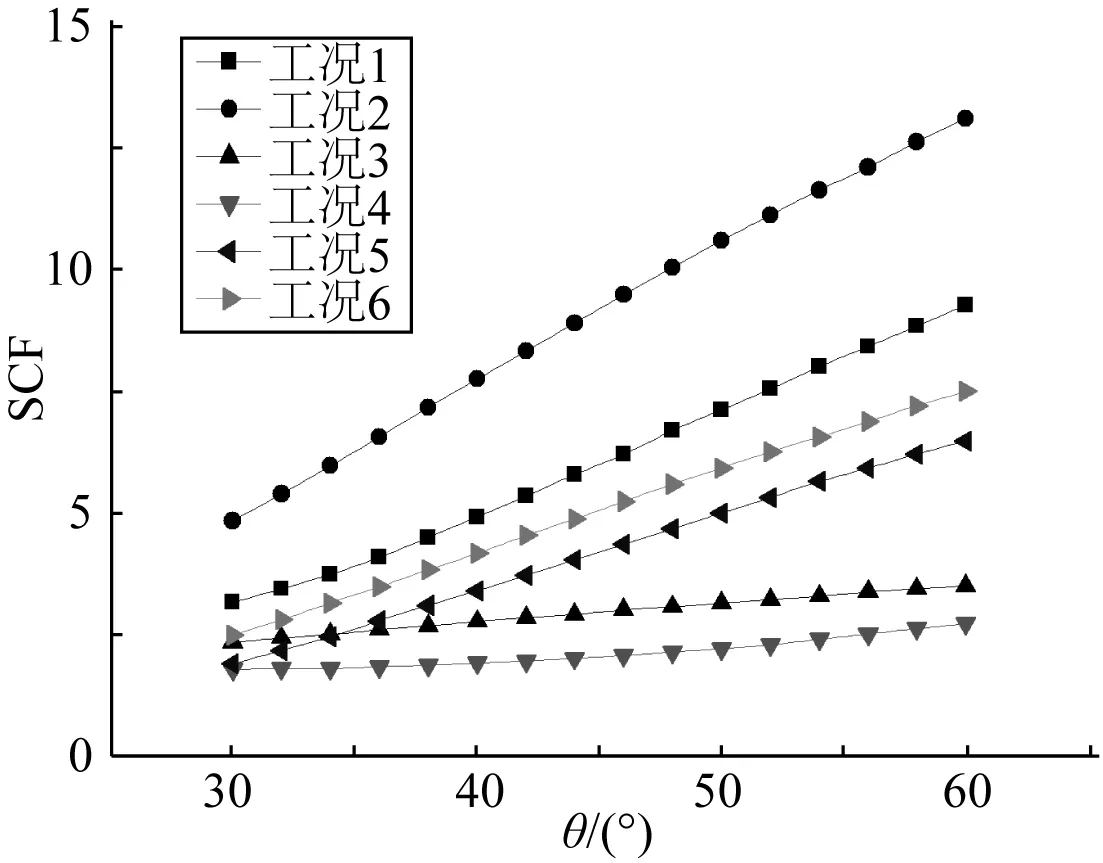
图12 KK型管节点SCF随θ的变化Fig. 12 Variation of SCF with θ of KK tubular joints

从图12可以看出弦杆轴线与撑杆轴线的夹角θ对KK型管节点SCF的影响为：① 在所有工况下，SCF均随着θ的增加而增加，因此采用较小的θ是比较合理的; ② 在工况1、2、5和6时，SCF随着θ的增加而明显增加; ③ 在工况3和4时，SCF随着θ的增加而略微增加; ④ 在工况2时，即撑杆均承受轴向拉伸的作用时，SCF值较相同θ下其他工况的SCF值大，由θ为30°时的4.83增加到θ为60°时的13.11，增加了171.43%; ⑤ 综合比较工况3、4、5和6，撑杆承受面内弯矩My作用时的SCF值较承受面外弯矩Mx作用时的SCF值大，且随着θ的增加，差值越来越大。

θ不仅影响管节点的SCF，还对桩腿的布置、加工和钢材用量等有较大影响，因此在KK型管节点的设计中，应综合考虑这些因素并在满足其他各项要求的前提下，减小弦杆与撑杆的夹角θ，以提高管节点的疲劳寿命。

5 结 语

KK型管节点是海洋工程桁架式结构中所采用的一种管节点形式，其应力集中系数SCF是对管节点进行疲劳分析的重要参数。利用ANSYS软件对KK型管节点的应力集中系数SCF进行了分析，给出了SCF在不同无量纲参数下的几何敏感性分析结果，对其进行总结提炼得到以下规律：

1) 对于撑杆，承受轴向载荷时的SCF值较承受弯矩载荷时的SCF值大，承受面内弯矩作用时的SCF值较承受面外弯矩作用时的SCF值大;

2) 在满足其他条件的前提下，取较小的α、β、γ、τ、θ对撑杆疲劳有利，即对撑杆取较小的直径和较小的厚度，而对弦杆取较大的直径和较大的厚度，且β尤其不应超过0.4，同时适当减小弦杆与撑杆的夹角对疲劳有利;

3)ξ与撑杆之间的间隙相关，SCF的大小与撑杆受载形式呈非线性关系，故ξ应综合考虑撑杆载荷的作用形式以及生产施工等因素来确定；

4) 管节点结构形式设计是一个综合性的设计，需要考虑结构布置、加工建造工艺、屈服强度、屈曲强度、疲劳强度以及经济性等。在满足其他条件的基础上，合理调整KK型管节点的几何参数，不仅可提高该类型管节点的疲劳寿命，同时还可以达到优化结构、降低成本的目的。