超几何-正态模型在稀疏二分类数据Meta分析中的应用及R软件实现
张天嵩
本文介绍Stijnen等[1]提出的超几何-正态模型(hypergeometric-normal model,HNM),并实例说明采用R软件拟合该模型的具体方法和步骤。
1 方法
1.1 研究数据 数据来源于一项Meta分析[2],该研究主要观察β受体阻滞剂对充血性心力衰竭的干预作用,本研究选择测量结局为病死率的相关数据,表1显示,纳入的22个研究中,有2个单零研究、5个双零研究,共含有7个变量。
1.2 模型与方法[1]假设纳入Meta分析第i(i=1,2,…,N)个研究第k(k=0,1)个臂的事件发生人数和总人数分别为rik和nik,每个臂的事件发生率为pik,单个研究的真实值为θi,估计值为yi,估计值的标准误为Si,研究间真实效应变异为τ2,总的合并效应为θ,则经典的正态-正态模型有2层,第1层为抽样模型,又称为研究内模型,假定yi服从未知均值θi和已知标准误Si的正态分布:yi~N(θi,Si2);第2层为参数模型,也称为研究间模型,假定θi服从正态分布:θi~N(θ,τ2)。如果选取OR的对数尺度为效应量,

如果四格表中有1个数据为0,则无法计算标准误。一般情况下每个格子加0.5进行连续性校正,但合并结果可能产生偏倚。因此,为避免近似正态研究内似然的潜在问题,Stijnen等[1]建议用给定研究中事件总数ri=ri0+ri1的精确条件似然如非中心超几何分布来代替它:

与参数模型合称为HNM。该模型实质上是条件Logistic回归混合效应模型,在计算方面比较困难,可以采用SAS软件的NLMIXED程序、R软件的meta包及metafor包等实现。
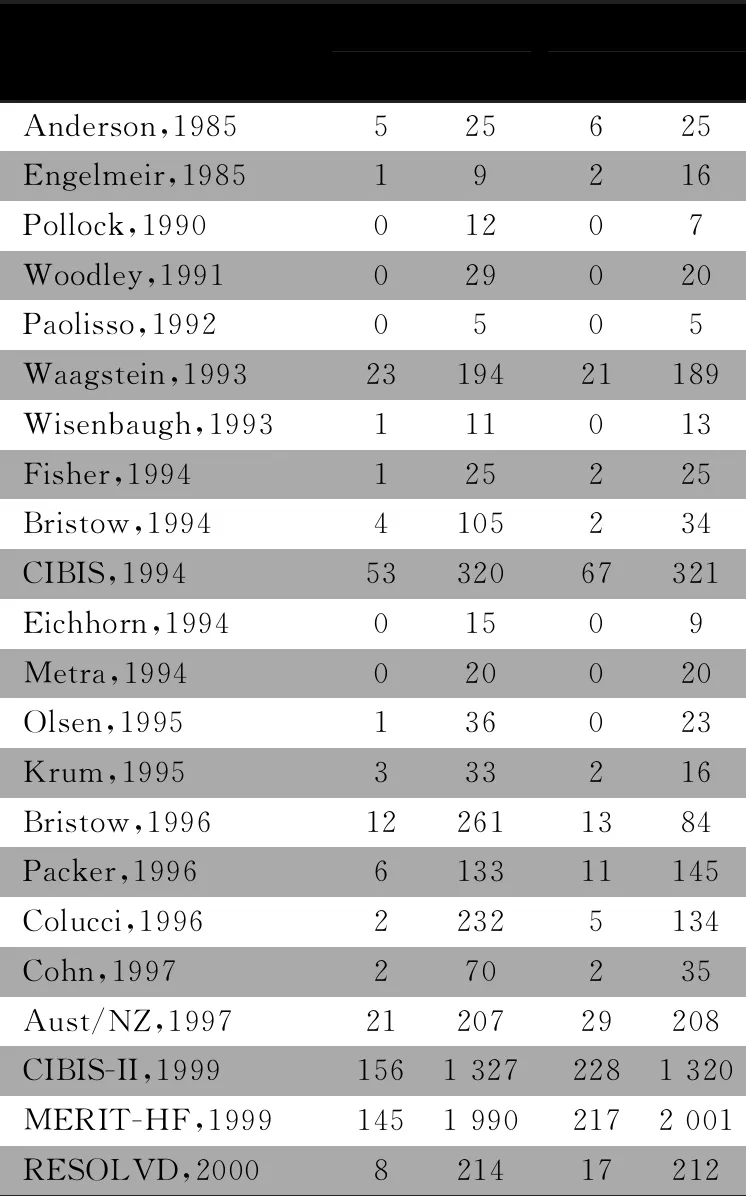
表1 β受体阻滞剂治疗充血性心力衰竭的
1.3 模型拟合 重新分析Beophy等[2]研究的数据,选取OR为效应指标,采用R4.0.0软件的meta包(version 4.14-0)中的metabin()函数以确切似然法拟合HNM。
需注意,metabin()函数在默认设置下,不显示双零研究等单个研究的效应量点估计及95%CI,可以通过设置“allstudies=TRUE”参数将双零研究进行连续性校正,再计算单个研究结果;以print()函数打印主要合并结果,并通过forest()函数绘制森林图,具体过程如表2所示。

表2 拟合模型过程及简要解释
2 结果
meta包metabin()函数拟合HNM,针对研究间异质性检验提供了2种方法,结果分别为,Wald检验Q统计量为54.1,相应P< 0.001;似然比检验Q统计量为59.69,相应P< 0.001。研究间异质性方差为0.188 9,方差的标准差为0.434 6;I2统计量为62.6%;H统计量为1.63。
主要合并结果如图1所示,固定效应模型和随机效应模型OR及95%CI分别为0.49(0.42~0.56)、0.54(0.39~0.75)。
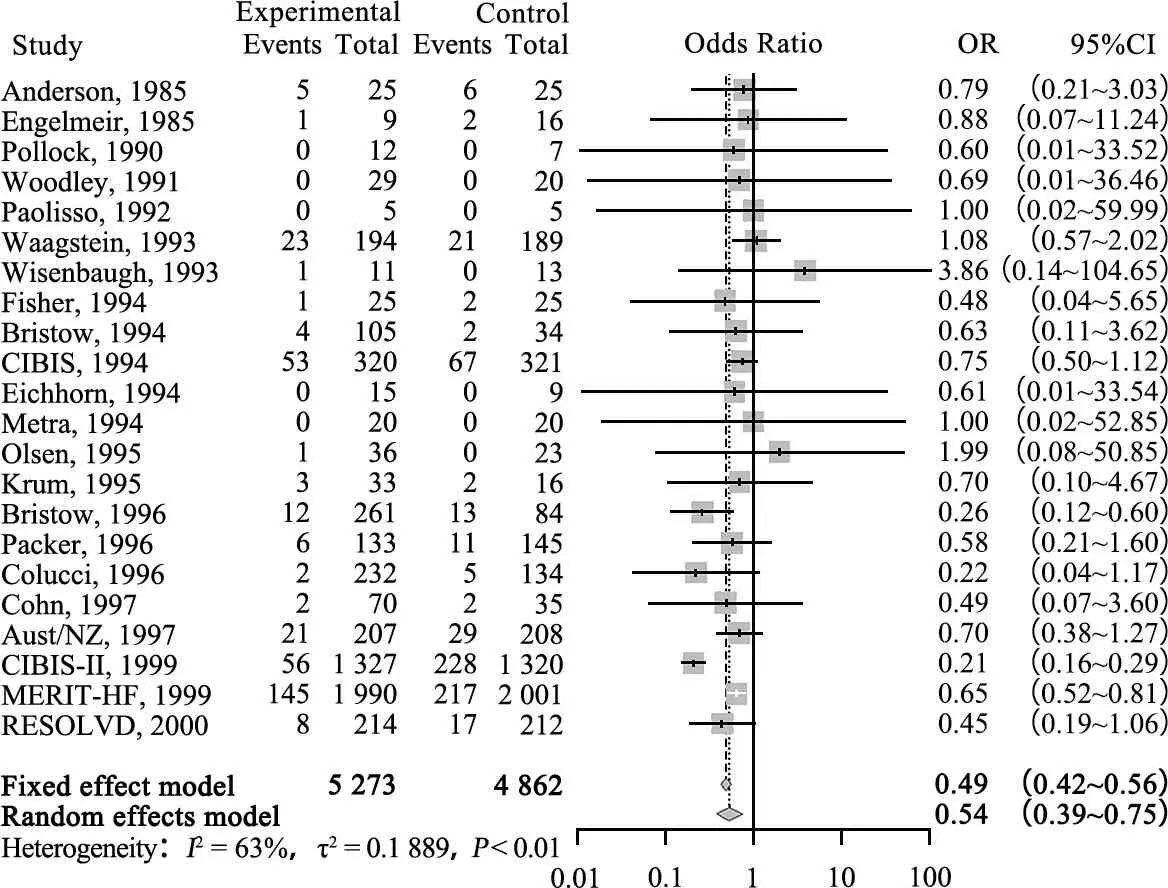
图1 森林图
3 讨论
在医学领域内,Meta分析中涉及稀疏二分类数据的现象十分常见,如一项对500篇Cochrane系统评价随机抽样调查的研究表明,有30%的系统评价中至少有1个研究1个臂的事件发生数为0[3]。针对稀疏二分类数据Meta分析, Peto法、Mantel-Haenszel法等一般经典方法是对单零研究进行连续性校正(如对四格表数据每个格子的数据各加0.5),而将双零研究排除在外不进行合并;Logistic 回归虽然不需要对单零研究进行连续性校正,但将双零研究除外不纳入分析。无论是连续性校正还是除外双零研究,必然导致合并结果偏倚[1,4]。因此,涌现了一批新的模型和方法[4],如二项式-正态层次模型(BNHM)、贝塔-二项式模型(BBM)和HBM等,介绍相关软件实现的文献相继发表[5-8],为合并稀疏二分类数据提供了更为合理的分析策略。
Stijnen等[1]提出一种基于广义线性混合效应模型(GLMM)框架下确切研究内似然模型(EWLM),包括二项式-正态模型(BNM)和HNM等,并给出SAS软件NLMIXED程序拟合模型的代码,吴敏等[5]将该模型在国内进行了介绍,并补充了MIXED和NLMIXED等程序的相关代码,但SAS软件租赁费用昂贵,且需要使用者掌握一定的编程技术,因此限制了其使用和推广。基于软件可得性及模型拟合简易性等方面考虑,推荐使用R软件。R软件中meta、metafor等核心Meta分析包均可以拟合HNM,其中meta包中的metabin()函数内部调用metafor包的rma.glmm()函数,因此,2个包获得结果完全一致,本文结果与原文采用的贝叶斯层次随机效应Meta分析模型获得的结果0.65(0.53~0.80)相近[2]。
需要注意的是,用于罕见事件 Meta 分析的不同模型和方法可能导致不同结论,且数据越稀疏,不同方法结果间差异越大。因此,笔者建议系统评价员在制定系统评价/Meta分析计划时就应考虑,如果遇到稀有数据时,应选择多种分析方法进行敏感性分析,以确定结果是否稳健[6]。

