地震作用下简支梁桥纵向碰撞模拟

游四方，郑史雄，贾宏宇，赵灿晖，杨光强，杨 健

(1.西南交通大学土木工程学院，成都 610031；2.贵州理工学院，贵阳 550003； 3.贵州省交通规划勘察设计研究院股份有限公司，贵阳 550081)

我国地处亚欧板块和太平洋板块交界处，地震频繁且威胁巨大。2008年四川汶川地震、2010年青海玉树地震、2013年四川雅安芦山地震以及2014年云南昭通地震，均造成了重大的生命财产损失和桥梁碰撞事故[1]。简支梁桥作为桥梁结构中的重要桥型之一，因约束、受力及结构布置简单而被广泛使用。基于简支梁本身的结构特点，往往要在梁间设置伸缩缝以抵抗温度等因素导致的纵向变形，由于这个间隙的存在，使梁间碰撞破坏成为一种普遍现象。

地震作用下桥梁结构的碰撞问题层出不穷。1989年美国洛杉矶Loma Prieta地震China Basin高架桥的一个截面处因上下路面间的立柱间距预留较小而发生碰撞，使桥面和桥墩发生脆性破坏[2]；1995年日本Kobe地震，一座高速公路桥桥面产生0.03 m顺桥向位移，导致支座和连接限位构件失效，梁间发生碰撞破坏[3]；2008年汶川地震，百花大桥因纵向位移过大而发生落梁破坏，导致第5联整体倒塌[4]。基于以上事实可知，梁间碰撞已成为桥梁损坏甚至是倒塌的重要因素。针对此类桥梁事故，国内外学者进行了大量研究，于海龙[5]分别在2跨和3跨简支梁桥上作用不同的地震波，证实碰撞效应对桥梁结构的显著响应；陈彦江等[6]以3跨简支梁桥为例研究了接触单元刚度、伸缩缝间隙、墩高比对桥梁响应的影响；贾宏宇等[7]用虚拟激励法对高墩桥梁的碰撞可靠度问题进行了研究，并推导出碰撞概率和地震峰值加速度之间的变化关系，结果表明：地震加速度大小与碰撞动力可靠度成反比；贾宏宇等[8-9]基于随机振动理论提出了震级-间隙宽度的计算方法，在此基础上研究了不同场地与间隙宽度的关系，该结果可对新设计桥梁和既有桥梁间隙大小进行指导和评估；黄宇辰[10]对摩擦摆半径和支座摩擦系数进行了研究，结果表明,横向地震作用对梁间碰撞是不利的，增大摩擦摆半径和摩擦系数可以减小地震反应；彭刚辉等[11-12]从隔震支座的温度和时效两个方面对碰撞效应进行研究，指出低温环境下简支梁桥应选择耐寒性强、隔震效果好的支座；此外，为证实地震动的空间性对大跨桥梁的不利影响，Hao H[13]通过建模分析和数值模拟，从地震动的空间作用、跨度和阻尼等方面进行碰撞研究，结果表明,地震动空间效应是导致梁间碰撞的重要因素；Bi K和Hao H[14-15]通过随机振动理论研究了桩-土相互作用对简支梁桥碰撞间隙的影响，证实在软土条件下桩-土相互作用对碰撞间隙有不可忽略的影响；李兰平等[16]提出了一种考虑局部场地效应、相干效应和行波效应的多点激励反应谱分析的改进方法，并证实地震动的空间性对大跨度桥梁的重要影响。

近年来，我国高铁和公路大量兴建，尤其是高铁大量采用“以桥代路”设计，这也导致大量的梁式桥涌现出来，但由于目前对此类桥梁在高烈度地震区的抗震性能的研究还不够深入，客观上还需要加强这方面的研究，并指导抗震规范的不断完善。针对这个问题，结合以上学者的研究成果，以一座3跨高速铁路简支梁桥为背景，建立其在纵向地震波作用下的三维有限元碰撞模型，并在有限元软件SAP2000中进行非线性动力分析，探究伸缩缝间隙大小、碰撞刚度大小、桥墩高度以及行波效应等因素对桥梁动力响应的影响。

1 碰撞作用理论分析模型

目前关于桥梁碰撞的研究方法主要有3种：恢复系数法、拉格朗日乘子法和接触单元法。模拟行波效应也有3种方法：大质量法、大刚度法和直接方法。限于篇幅，此处仅对本文所用的接触单元法和大质量法进行介绍。

1.1 接触单元法

接触单元法的作用原理是在会发生碰撞的相邻梁端连接一个接触单元，当相邻主梁梁端的相对位移达到伸缩缝间隙时，就会发生碰撞。目前而言，接触单元的模型种类有很多，例如线性弹簧单元、Kelvin模型、Hertz模型、Hertz-damp模型、三维接触-摩擦模型，其中前两种适用于线性情况，后两种用于解决非线性问题；线性弹簧单元和Hertz模型未考虑能量损失，Kelvin模型和Hertz-damp模型需要考虑阻尼的影响。此外，不同模型的精度及计算复杂程度也不尽相同，在实际的碰撞模拟中应根据情况选择合适的模型。

为较为真实地模拟碰撞过程中碰撞力和梁间变形之间的关系,以及碰撞过程中的非线性接触问题，本文选用Hertz模型进行碰撞模拟分析。其中Hertz模型的碰撞力表达式为

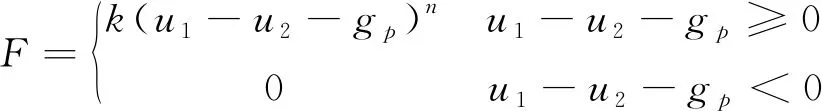
(1)

式中，k为连接弹簧的非线性刚度；n为该刚度的变化趋势，通常取1.5；u1,u2为两相邻跨主梁的位移；gp为两相邻主梁之间的距离[17]。

1.2 大质量法

大质量法是通过对支承点(本文中即桥墩底部4个固结点)施加力的时程，使得支点处的大质量产生振动，从而实现各支承点的非一致地震激励的一种方法，桥梁系统的运动方程如下

(2)

2 工程实例及其模拟

以一座3跨高速铁路简支梁桥为工程背景，主梁截面宽12.6 m，桥边不设置人行道以及其他附属设施，不考虑有砟轨道的影响，计算跨径31.5 m，全梁长32.6 m，横截面采用单箱单室等高度简支箱梁，箱梁高3.035 m，梁端顶板、腹板、底板在梁端1.5～4.5 m的3 m范围内进行局部内侧加厚，主梁梁体混凝土强度等级为C50；主梁支座横向中心距4.5 m，支座对主梁的支撑长度为0.55 m。桥墩截面采用椭圆形，桥墩自墩顶0～2.75 m为变截面桥墩，再往下部分为等截面桥墩，桥墩墩身、托盘、顶帽混凝土强度等级均为C35。桥梁整体信息及布置情况如图1所示。

图1 3跨简支梁整体信息及布置情况(单位：mm)

对于该实例，采用有限元软件SAP2000进行模拟，其中主梁和桥墩单元均选用梁单元，梁间碰撞选择Gap连接单元，支座采用Wen单元，桥墩底部固结，不考虑桩土作用。

2.1 碰撞单元模拟

在SAP2000中选择Gap(缝单元)以实现梁间碰撞的模拟，恢复力模型如图1所示，碰撞力表达式如下

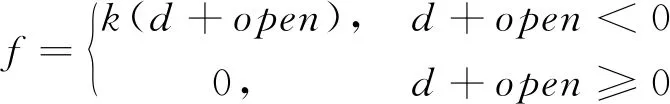
(3)

式中，k为弹簧的刚度；open为初始间距，d为轴向变形量。在进行碰撞间隙对桥梁响应的讨论时，依次取梁间间隙为0.05，0.06，0.07，0.08，0.09，0.10，0.11，0.12 m进行对比分析。

对于Gap碰撞单元中刚度的计算，常取相邻两跨中主梁较短的梁的轴向刚度值[18]，计算公式为

(4)

式中，A为主梁截面面积；L为主梁跨度。本实例中选初始碰撞刚度为1倍的主梁刚度。在进行碰撞刚度对桥梁响应的讨论时，依次取主梁刚度的0.4，0.6，0.8，1.0，1.2倍。

2.2 支座单元模拟

盆式橡胶支座普遍应用于现代城市桥梁设计中，故本文按照图纸要求，同时参考《城市桥梁抗震设计规范》中的相关规定，用双线性理想弹簧单元模拟盆式橡胶支座，其恢复力模型见图2。

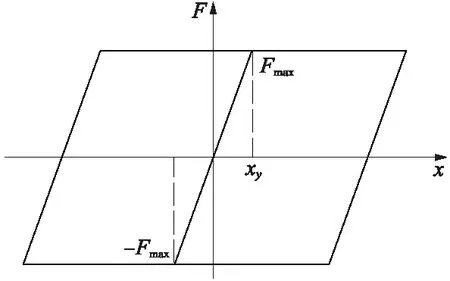
图2 恢复力模型

盆式活动支座临界滑动摩擦力

Fmax=μdR

(5)

支座初始水平刚度

(6)

支座竖向刚度

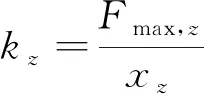
(7)

式中，μd为滑动摩擦系数，该值一般取0.02；R为上部主梁的自重荷载，kN；xy，xz为屈服位移，m，该值常取0.002～0.005 m。

在软件中使用Wen单元塑性属性模拟支座，力的表达式为

f=r·k·d+(1-r)·y·z

(8)

式中，k为弹性弹簧常数；y为屈服力；r为屈服后刚度和弹性刚度之比；z是内部滞后变量。

(9)

公式中，exp为不小于1的指数，该指数数值越大，屈服比率越陡，实际该指数最大取20，见图3。

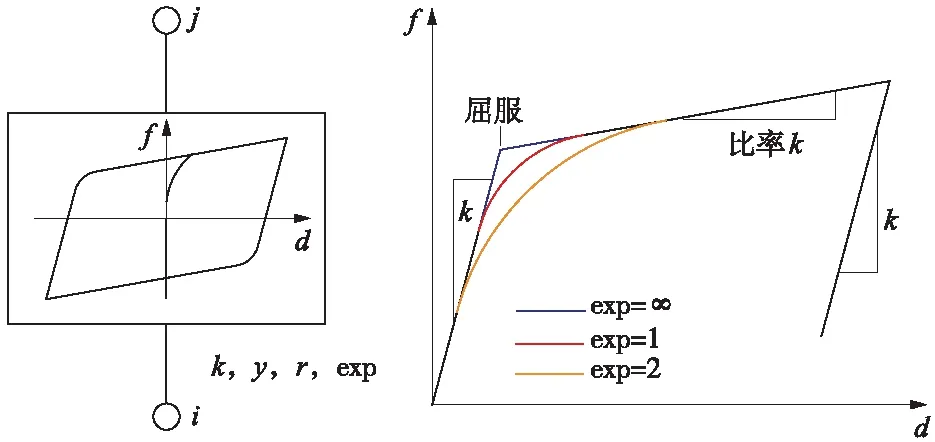
图3 Wen单元塑性属性

主梁支座情况依据图纸要求，在模拟操作中进行位移约束，如图4所示(图中箭头表示为支座可以朝该方向发生移动)。

图4 支座约束

2.3 地震荷载模拟

选取人工合成的罕遇地震波，并同时施加在桥墩底部(一致激励)，峰值加速度为4.524 m/s2，时程曲线如图5所示。

图5 地震加速度时程

再对该地震荷载进行傅里叶变换，结果如图6所示，其中出现3个典型的频率峰值，分别为6.3，8.5，21.8 Hz。

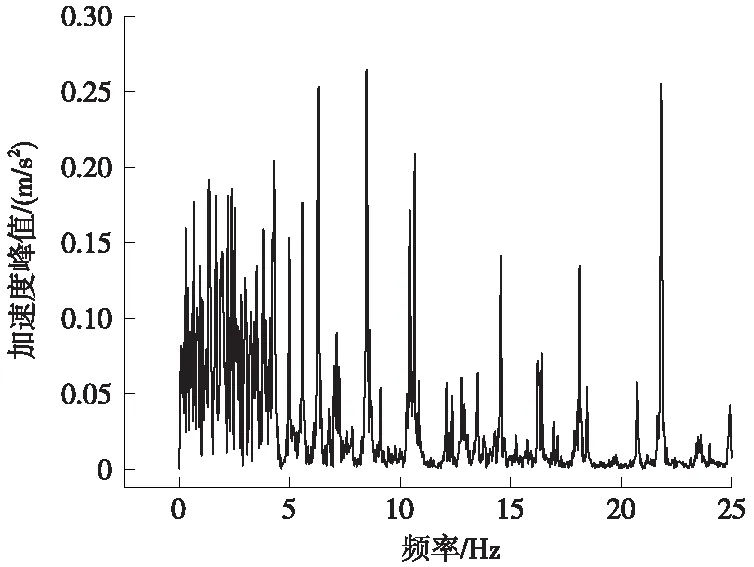
图6 傅立叶变换

3 计算分析

3.1 模态分析

基于SAP2000中的Rite向量法对桥梁模型进行自振特性计算分析，各阶振型频率及振型特点如表1所示。

表1 桥梁动力特性

此结果和傅立叶变换的结果进行比对可知，该桥前5阶振型的自振频率均在5.5～6.8 Hz，接近外荷载频率，容易引发桥梁共振现象，加重震害。

3.2 碰撞与否对结构动力响应的影响

选取初始碰撞间隙为0.12 m进行模拟(当碰撞间隙超过一定值时便会因间隙过大而不发生梁间碰撞)，碰撞刚度为k(主梁刚度)，桥墩高度均为12.75 m，选取2号桥墩为研究对象，数据结果见图7。

图7 考虑碰撞与否时的各响应

图7(a)结果显示，整体上看，考虑碰撞时墩底弯矩与未考虑碰撞时差异并不大，但最大值增加了34.5%，即碰撞的发生使得墩底响应有所减小，避免墩底应力较大而造成的不利影响；图7(b)显示，梁端位移在两种情况下重合度较高，但不考虑碰撞时的梁端位移最大值要大13%。基于这样的数据结果，在实际工程应用中更要考虑桥梁结构的碰撞问题，以防止强震作用使得梁端位移大于支座支撑长度而发生落梁破坏。

3.3 改变碰撞间隙的影响

为探究碰撞间隙对结果的影响，保持桥墩高度为12.75 m，碰撞刚度为k(主梁刚度)，改变碰撞间隙的大小，依次对0.05，0.06，0.07，0.08，0.09，0.10，0.11，0.12 m这8种情况进行分析，选取2号桥墩为研究对象，结果见图8。

图8 考虑碰撞间隙的各响应

从图8(a)可知，碰撞力对间隙值的变化十分敏感，间隙值取50 mm时的碰撞力约为60 mm时的2.5倍，为70 mm时的10倍，碰撞力的大小随着间隙的增加有减少趋势；图8(b)表示的墩底最大弯矩在较小的间隙值时有较大的响应。总的来说，桥梁响应均随碰撞间隙的增加而减小，在碰撞间隙值取90 mm时，各响应均保持在较低的水平。故选择合适的间隙值可以降低梁间碰撞引发的不利影响。

3.4 碰撞刚度影响

为探究碰撞刚度对结构响应的影响，保持桥墩高度为12.75 m，碰撞间隙为0.10 m，选取碰撞刚度为0.4k、0.6k、0.8k、1.0k、1.2k五个样本进行分析，并以2号桥墩为研究对象，数据结果见图9。

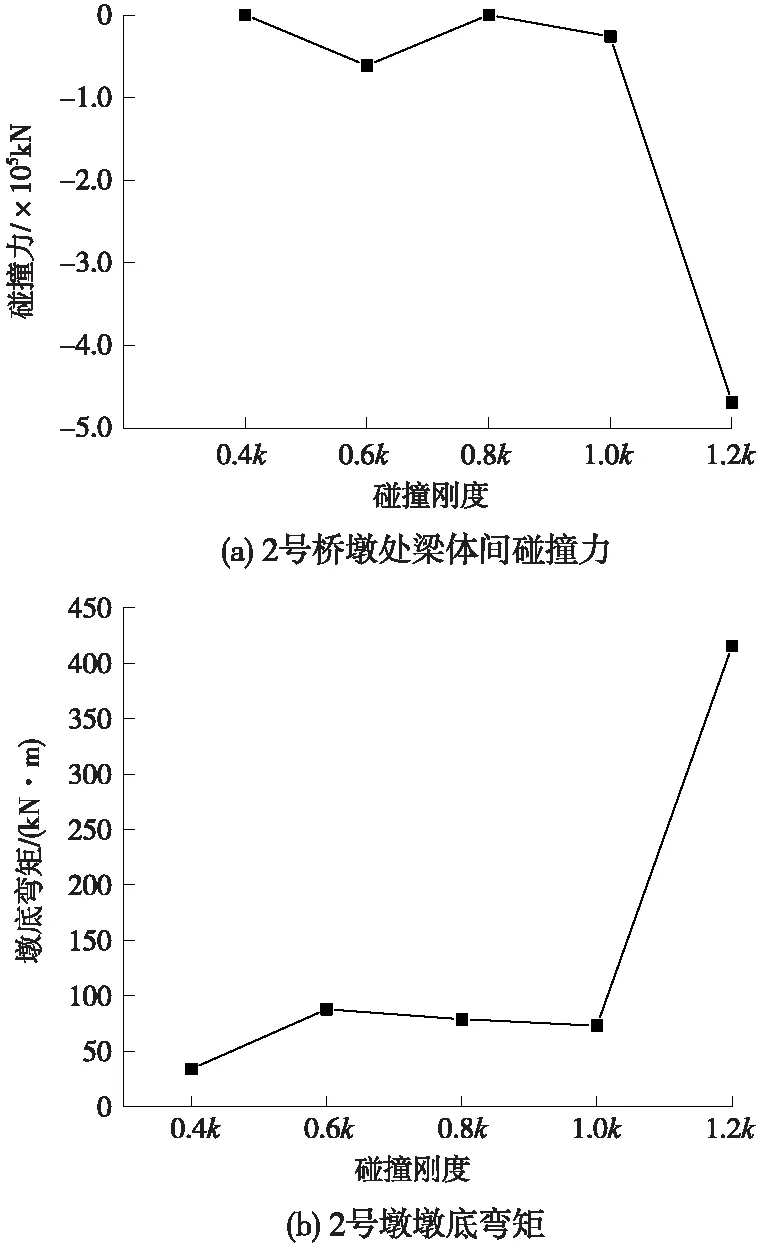
图9 考虑碰撞刚度的各响应

据图9分析，在碰撞刚度小于1.0k时，碰撞力、墩底弯矩均处于平稳变化阶段。考虑到整体稳定以及协调左右两跨主梁振动以及降低梁间碰撞等因素，可以保持碰撞单元刚度和两侧较短主梁刚度一致，以获得较为安全的结构响应。当碰撞刚度大于1.0k时，各响应均发生了较大的突变，造成这样的原因是刚度过大使得梁间接近于刚性连接，使桥梁的振动模态和碰撞单元的受力变得复杂所致。

3.5 桥墩高度影响

为探究桥墩高度对结构响应的影响，保持碰撞刚度k和碰撞间隙0.10 m不变，依次改变3号桥墩的高度为10.75，12.75，14.75 m，墩高比(3号桥墩高度与2号桥墩高度的比值)分别为0.84，1.00，1.16，选取2号桥墩为研究对象，数据结果见图10。

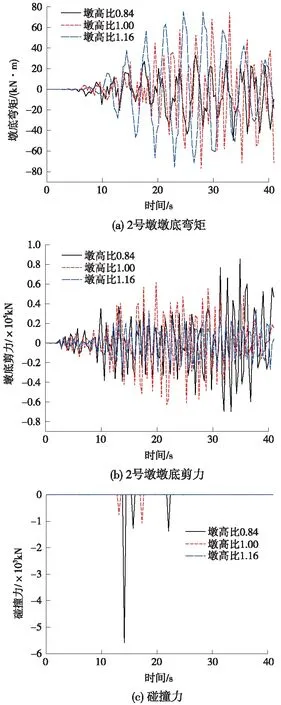
图10 考虑桥墩高度时的各响应

对2号墩而言，随着墩高比的增大墩底弯矩在不断增加，墩底剪力在不断变小，梁间碰撞力在墩高比为1时结果最优。当墩高比为1.00～1.16时的墩底弯矩分别比墩高比为0.84时增加了71.7%，73.5%，墩底剪力则变为墩高比为0.84时的53.9%，39.5%。容易发现：桥墩较高时桥墩的控制因素是墩底弯矩；桥墩较矮时则是由墩底剪力控制；保持墩高一致，使得相邻两跨动力特性接近，可以降低梁间的碰撞作用。

3.6 盆式支座连接方式对碰撞的影响

考虑到支座连接方式的差异，每一跨主梁左右两端盆式橡胶支座的约束方向(图4)是不同的，这样的差别会对下部桥墩和主梁单元产生不同程度的影响。基于这种考虑，这里选择2号、3号桥墩进行对比分析，数据结果见图11。

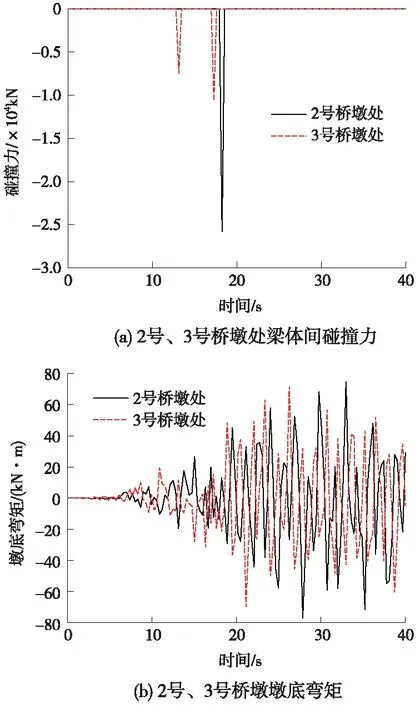
图11 考虑支座连接差异的各响应

图11(a)的碰撞力中显示2号桥墩处的梁端碰撞力是3号桥墩处的梁端碰撞力的2.5倍，根据图4中的支座布置情况有以下思考：2号桥墩处的PZ-5000-ZX支座和PZ-5000-DX支座，均没有限制纵桥向位移，而3号桥墩处的PZ-5000-GD支座和PZ-5000-HX支座，则对纵桥向位移进行了限制，因此前者的主梁梁端位移大于后者，碰撞力也有这样的变化；图11(b)中两个桥墩的墩底弯矩差距不大，从而可以认为盆式橡胶支座的不同连接方式对梁端碰撞力有较大的影响，对桥墩单元的影响不大。

3.7 行波效应影响

地面的运动不仅是随时间发生变化的，而且还有明显的空间效应，包括有部分相干效应、局部场地效应和行波效应。这些因素会导致不同位置的桥墩在同一时刻发生激励不尽相同。

对跨度较小的桥梁结构，不同桥墩受到的激励差别不大，可忽略地震波的空间变化特征。但对于跨度较大的桥梁结构而言，由于地震动空间效应的影响，不同支撑点的地震波输入变化会很大，振幅和频率也不同，这将导致结构产生不同的桥梁结构动力响应。故对于大长结构的多跨简支梁，有必要考虑行波效应对结构动力响应的影响。

在本文中选择4个不同的视波速来探究行波效应对简支梁纵向碰撞的影响，视波速分别为500,1 000,1 500 m/s和无穷大(一致激励)，其他各参数保持不变，数据结果见图12。

图12 不同视波速下2号桥墩各响应

图12为各视波速下2号桥墩处各响应的结果。分析可知，无论是梁端碰撞力、墩顶位移还是桥墩底部弯矩，均随着视波速的增加而减小。且视波速越小，结构动力响应变化越剧烈；视波速越大，结构动力响应越趋于平稳，此时结果也越接近一致激励的情况。

此处还可以得出以下结论：在实际情况下，当桥梁的跨度较大，视波速的大小对桥梁动力响应会产生比较明显的影响，而且视波速越小响应越大。这是因为在较小的视波速作用下，不同位置处的桥墩在同一时刻受到的激励不相同，并且差异较大，这样便导致结构的响应有较大差别。当视波速不断增大时，这种差别就会有不同程度上的减小，并逐渐趋于一致激励时的结果。

4 结论

以有限元软件SAP2000为平台，分别建立了各参数影响的对比模型，通过计算分析后得出如下结论。

(1)考虑碰撞时的墩底剪力要比未考虑时大，梁端位移最大值也在地震加速度较大时增大了13%，落梁破坏比不考虑时更容易发生；碰撞间隙对梁间碰撞力起控制作用，间隙值不同碰撞力差异较大，大小也会随着间隙值的增加而减小；碰撞刚度在小于主梁刚度时，响应稳定，当超过主梁刚度时会发生突增。

(2)桥墩高度决定了在地震作用下桥墩是受弯矩还是剪力控制：桥墩较高时桥墩的控制因素是墩底弯矩，桥墩较矮时则是由墩底剪力控制，保持墩高一致使得相邻两跨动力特性接近，可以降低梁间的碰撞作用；不同的支座连接方式导致纵向约束的不同，仅对梁间碰撞力影响较大，对桥墩的影响较小。

(3)考虑地震动的空间作用行波效应对桥梁结构的影响，在较小视波速下的结构反应是大于较大视波速下的结构响应，而且视波速越大，越接近于一致激励的情况，在进行大跨度桥梁设计时应予以注意。