风力机叶片翼型钝尾缘改型新方法及气动性能分析研究

马铁强， 陈 明， 孙传宗

（沈阳工业大学 机械工程学院 风力机械传动与控制实验室， 辽宁 沈阳 110870）

0 引言

翼型是构成风力机叶片的基本元素， 翼型的气动性能决定了叶片的气动效率， 进而影响风电机组的输出功率。开发新的翼型系列耗时长、投资大，在现有翼型基础上，通过调整和优化翼型结构来提高翼型的气动性能较为稳妥。 在翼型上安装Gurney 襟翼、楔形块或者对翼型尾缘进行修型处理可以使翼型升力系数明显提高。 随着风力机功率的逐渐增大和叶片长度的增加， 对叶片的要求也越来越高。 考虑到大型风力机叶片的强度和工艺，叶片的中部和根部通常为钝尾缘的形式，如荷兰DU 系列翼型。 国内外学者针对钝尾缘以及尾缘改型的翼型进行了大量的试验和数值上的研究。 由于气动和结构上的优点[1]，一般情况下，钝尾缘风力机翼型满足0.2＜r/R＜0.42[2]，并常被用于大型叶片设计之中。 翼型尾缘加厚主要有对称加厚法、非对称加厚法和直接截断法[3]，[4]。 尾缘加厚翼型的升力系数比原始翼型有一定的提高， 且受前缘粗糙度的影响小于原始翼型[5]，同时大大推迟了翼型的失速现象[6]，尾缘加厚的翼型可同时兼顾结构与气动性能要求[7]。 尽管加厚尾缘翼型可以提高升力系数， 但其带来的阻力大幅增加是不可忽略的。 考虑到尾缘厚度增加所带来的对阻力影响， 本文提出了翼型尾缘弧形加厚法。 通过CFD 方法对尾缘厚度不同的翼型和翼型尾缘弧形加厚法改型的翼型进行气动性能计算。

1 研究对象

荷兰Delft 理工大学在欧盟JOULE 计划和荷兰能源与环境局的资助下， 开发了DU 风力机翼型族[8]。 DU 翼型的设计原则是外侧翼型具有高升阻比、高的最大升力及缓和的失速特性、对粗糙度不敏感和低噪声。内侧翼型适当满足上述要求，重点是考虑结构要求和几何兼容性。 与传统航空翼型相比，对DU 翼型上表面厚度进行了限制，且具有较低的粗糙度敏感性。本文选用相对厚度为21%的DU93-W-210 翼型。 此翼型已在Dleft 理工大学低速风洞进行了性能测试，测试结果见文献[8]。

2 数值方法

2.1 计算网格

计算网格由CFD 前处理软件ICEM 生成。 对于钝尾缘翼型，由于尾缘较厚，一般使用O 型网格。对于尖尾缘的翼型，一般使用C 型网格。本文翼型多为钝尾缘翼型， 所以生成O 型拓扑网格，并对翼型尾缘的尖角做光顺处理，如图1，2 所示。为了准确模拟边界层内的流动，使得近壁Y+＜1，翼型表面第一层网格高度设置为5E-6 倍弦长，法向网格增长率为1.2， 翼型表面网格节点数为430，尾迹与前缘网格数为100，垂直壁面网格数为230，远场为30 倍弦长。

图1 DU93-W-210 翼型计算网格Fig.1 Computational grid for the DU93-W-210 airfoil

图2 DU93-W-210 翼型尾缘部分计算网格Fig.2 Calculation grid for the trailing edge part of the DU93-W-210 airfoil

2.2 数值方法及适应性验证

本文采用CFD 软件Fluent 对各种原始翼型及其尾缘改型翼型进行数值计算。 基于雷诺时均方法（RANS）对二维翼型进行数值计算。本文中所有翼型的弦长均为1 m，雷诺数Re=2×106，相对来流速度为29.561 m/s。 湍流模型选用Transition k-ω SST 湍流模型，该模型是转捩模型与k-ω SST模型的组合。k-ω SST 模型是全湍流模型，适用于前缘受污染的翼型， 而带转捩修正的湍流模型适合计算光滑翼型的气动性能。

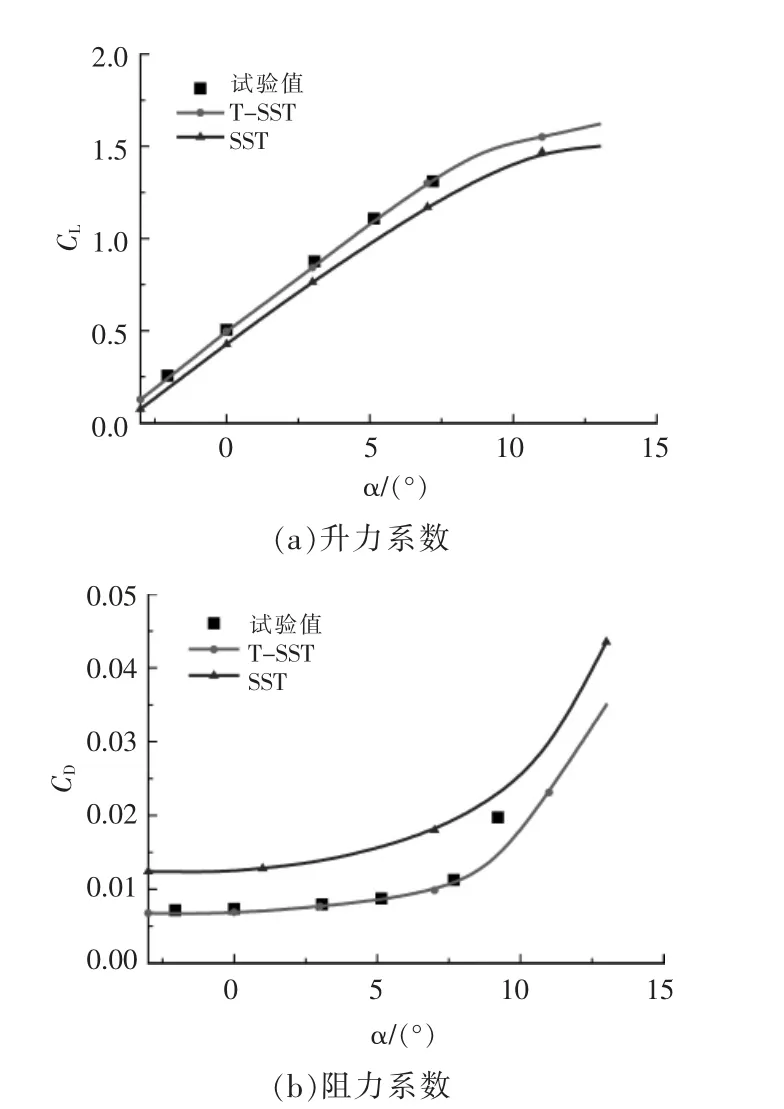
图3 不同湍流模型下DU93-W-210 翼型计算值与试验值对比Fig.3 Comparison of calculated and experimental values of DU93-W-210 airfoil under different turbulence models

DU93-W-210 翼型是Delft 理工大学在1993年设计的DU 翼型系列之一，该翼型已在Dleft 理工大学低速风洞进行了性能测试。 本文分别采用Transition k-ω SST 湍流模型和k-ω SST 湍流模型对其进行了数值计算，不同湍流模型下升、阻力系数随攻角α 变化的曲线如图3 所示。 由图3 可知：采用不同湍流模型时，升力系数CL随攻角变化的趋势均与试验值相同，采用Transition k-ω SST 模型时，CL与试验值吻合的较好，而采用k-ω SST 模型时，CL与试验值有一定误差，且低于采用Transition k-ω SST 模型时的CL； 采用Transition k-ω SST 模型时，阻力系数CD也与试验值吻合的较 好； 采 用k-ω SST 模 型 时，CD高 于 采 用Transition k-ω SST 模型时，但采用两种模型时的CD随攻角变化的趋势均与试验值相同。 所以本文采用Transition k-ω SST 湍流模型作为计算模型。

3 尾缘改型与计算结果分析

3.1 尾缘加厚法

翼型尾缘加厚主要有对称加厚法、 非对称加厚法和直接截断法等。 许多学者分析了钝尾缘翼型对风力机性能的影响。研究表明：尾缘加厚翼型的升力系数比原始翼型有一定的提高， 且受前缘粗糙度的影响小于原始翼型； 尾缘加厚的翼型可同时兼顾结构与气动性能要求。

本文选用对称加厚法对光顺翼型进行修改。目前，翼型尾缘对称加厚修型主要采用文献[3]提出的方法。 该方法在不改变基本翼型最大厚度和中线分布的前提下对称增加翼型尾缘厚度， 所增加的厚度服从幂函数分布。 幂函数分布可使改型后翼型的曲线比较光顺。 文献[9]提出一种尾缘对称加厚的翼型曲线公式，改型后坐标可写为

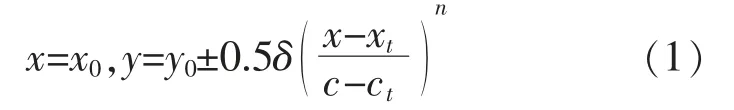
式中：δ 为需要增加的尾缘厚度；c 为翼型几何弦长； 下标t 为最大厚度位置；n 为幂指数， 随着n的增加，修改后的翼型更加贴近原始翼型，本文中n=2。

尾缘对称加厚部分的翼型轮廓如图4 所示。本文中尾缘增加的厚度分别为0.01c，0.02c，0.05c，0.07c， 尾缘增加的厚度对升力系数和阻力系数的影响如图5，6 所示。

图4 不同尾缘厚度对改型的影响Fig.4 Influence of different trailing edge thickness on modification

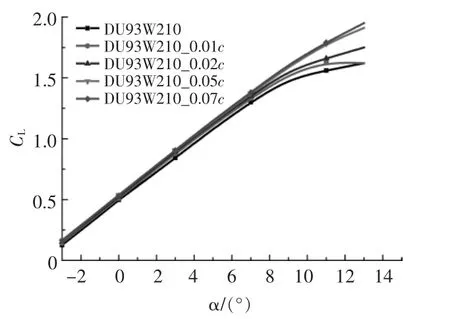
图5 不同尾缘厚度对翼型升力系数的影响Fig.5 The effect of different trailing edge thicknesses on the airfoil lift coefficient

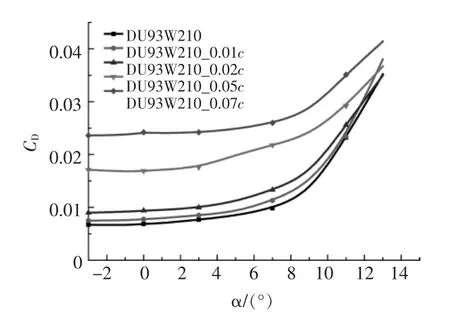
图6 不同尾缘厚度对翼型阻力系数的影响Fig.6 The effect of different trailing edge thickness on the airfoil drag coefficient

由图5，6 可知：尾缘加厚的翼型的升、阻力系数随攻角变化的趋势与原始翼型相同， 升力系数随尾缘厚度的增加而线性增加， 但这种效果并不明显； 阻力系数随尾缘厚度的增加而增加的效果十分明显。采用这种尾缘改型方法时，尾缘厚度增加所带来阻力增加的影响不可忽略。

3.2 基于翼型尾缘对称加厚修型与Gurney 襟翼结合的翼型尾缘弧形加厚法

考虑到Gurney 襟翼翼型的阻力较大，而采用指数混合函数对翼型尾缘修型后得到的翼型比较光顺。如果将翼型尾缘对称加厚修型与Gurney 襟翼相结合，不仅能提高翼型的气动性能，还能提高尾缘部分的强度。

本文基于文献[9]提出新的翼型曲线公式。 翼型上翼面坐标保持不变，下翼面采用幂函数加厚。设基线翼型坐标为（x0，y0），改型后的翼型坐标为（x，y）。

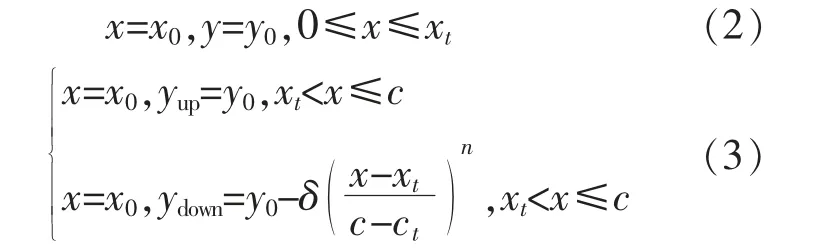
式中：yup为翼型上翼面y 坐标；ydown为翼型下翼面y 坐标；δ 为襟翼高度；xt为襟翼优化开始位置x坐标。

文献[10]认为，当n=1 时，翼型的气动性能有较明显的不连续，n 取1.8～2.5 较为合适。 由于本文所提出的方法不同于翼型尾缘对称加厚， 所以n 值分别取1，2，3，4，并对取不同n 值的改型后的翼型的气动性能进行对比，从而得出最佳的n 值。改型后的翼型的尾缘轮廓如图7 所示。 由图7 可以看出， 翼型尾缘弧形加厚法得到的翼型几何模型明显比Gurney 襟翼翼型光顺。采用这种改型方法的翼型的气动性能如图8，9 所示（δ=0.01c）。

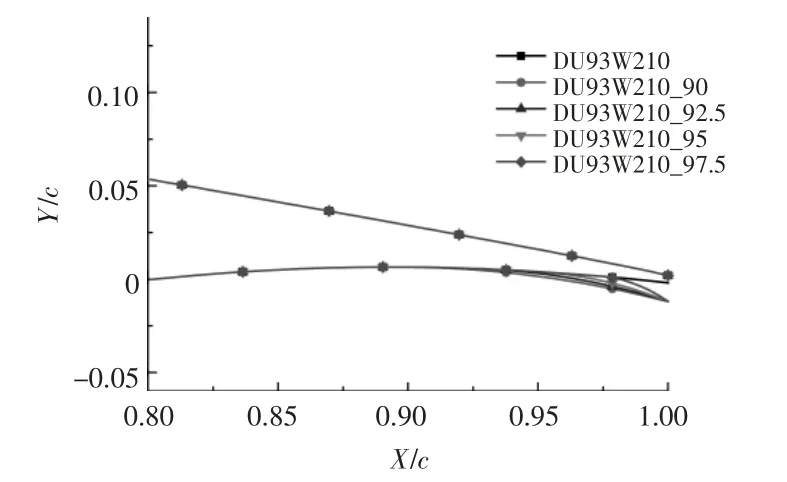
图7 不同改型开始位置对翼型外形的影响Fig.7 The effect of different modified starting positions on the shape of the airfoil

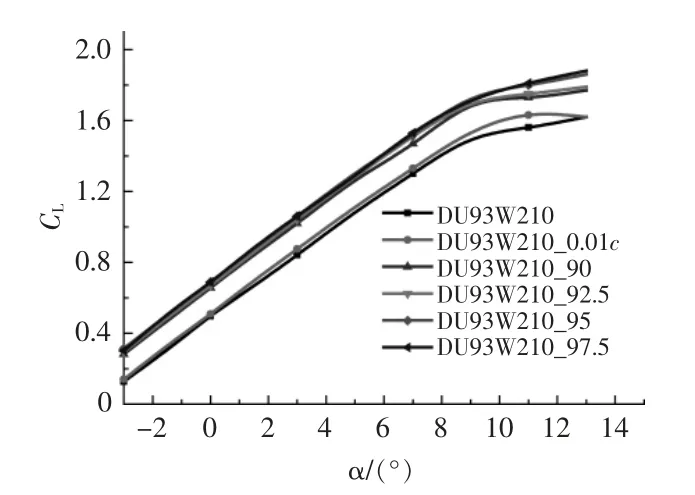
图8 不同改型开始位置对翼型升力系数的影响Fig.8 The effect of different modified starting positions on the airfoil lift coefficient

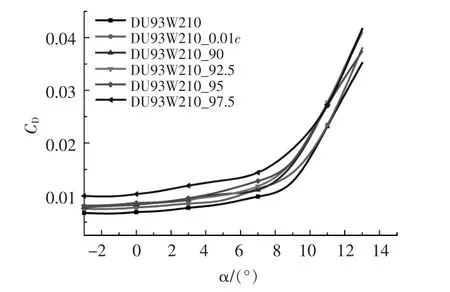
图9 不同改型开始位置对翼型阻力系数的影响Fig.9 The effect of different modification starting positions on the airfoil drag coefficient

由图8，9 可知：升力系数随改型位置的后移而增加，但这种增加并不显著；随改型位置的后移， 阻力系数也逐渐增加， 其中， 弦长90%，92.5%，95%处改型翼型的阻力系数与对称加厚翼型相差不多； 弦长97.5%处改型翼型的阻力系数明显增加，但其升力系数并没有明显的增加。 相对于尾缘对称加厚翼型的气动性能，采用这种方法改型的翼型气动性能更好。

3.3 n 对改型翼型气动性能影响

尾缘厚度δ 为0.01c，n 分别取1，2，3，4 时，92.5%处翼型尾缘弧形加厚改型的翼型气动性能如图10，11 所示。

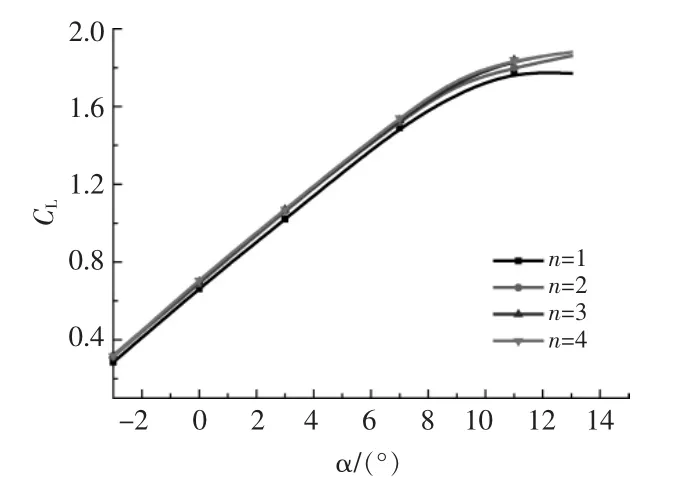
图10 不同n 值对改型后翼型升力系数的影响Fig.10 The effect of different n values on the lift coefficient of the modified airfoil

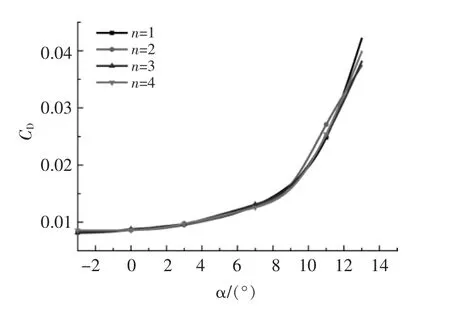
图11 不同n 值对改型后翼型阻力系数的影响Fig.11 The effect of different n values on the drag coefficient of the modified airfoil

由图10，11 可知：当n 值越大时，修型连接处的曲线越光滑；当n 值取2，3，4 时，升力系数略高于n 值取1 的翼型；n 值不同时，升、阻力系数相差不大。根据计算结果可知，n 值引起的改型翼型的气动性能变化很小。

4 结论

本文研究了两种不同的翼型尾缘改型方法，通过对DU93-W-210 翼型及改型的计算，得到以下结论。

①对称增加翼型尾缘厚度，随着尾缘厚度增加，升力系数相比原始翼型稍有提高，但阻力将大幅增加。 采用这种改型方法可以提高叶片结构强度，但同时带来的阻力增大不容忽视。

②采用翼型尾缘弧形加厚法修改翼型尾缘，对升力系数的提升极为明显，远远大于对称增加尾缘厚度法所提升的升力系数，阻力系数略大于尾缘对称加厚法的阻力系数，整体气动性能要优于对称加厚法改型的翼型。

③翼型尾缘弧形加厚法中，n 值对改型后翼型的气动性能影响不大，升、阻力系数只有微小的变化，n 值越大，改型连接处的曲线越光滑。