基于数据清洗与组合学习的光伏发电功率预测方法研究

邱 明， 鲁冠军， 吴昊天， 杨仲卿

（1. 重庆大学 能源与动力工程学院， 重庆 400044； 2. 重庆电力高等专科学校 动力工程学院， 重庆400053； 3.华北电力大学 电气与电子工程学院， 北京 102206）

0 引言

由于光伏发电系统具有可持续、 环境友好和发电效率较高等特点，因此，该系统越来越受到人们的重视。目前，我国光伏行业已进入了产业结构调整阶段， 各光伏企业均由原来的粗犷式发展模式转变为精细化发展模式。 2019 年，我国光伏市场结构调整初见成效， 分布式光伏电站和集中式光伏电站的占比逐渐趋于平稳， 光伏市场的发展状况也趋于稳定。 在如此大规模的光伏发电接入电力系统的情况下， 如何有效协调可再生能源和常规能源的规划与运行， 是当前可再生能源持续发展的关键问题。 可再生能源出力的不确定性给整个能源系统带来极大挑战。 因此， 须要对集中式、 分布式太阳能光伏发电系统的出力情况均进行 有 效 预 测[1]，[2]。

从上世纪70 年代开始，针对光伏发电功率预测问题，国内外学者已经展开广泛研究。光伏发电功率预测方法通常包括直接计算法和间接计算法。其中，直接计算法可基于气象参数变化过程计算得到光伏发电输出功率； 对于基于数据驱动的间接法， 使用机器学习模型对历史输出数据进行训练学习。间接计算法包括序列建模算法、支持向量 回 归（Support Vector Regressor，SVR）、神 经 网络（Artificial Neural Network，ANN）和混合建模方式[3]～[8]。文献[9]分析了目前常用的光伏发电功率预测方法，包括点预测和概率预测，并分别对当前的预测算法和评价指标等进行了梳理、归类和总结。文献[10]提出了一种分布式光伏电站预测模型，该模型使用临近区域的光伏电站进行建模， 使用长短期记忆网络对时间特征进行抓取， 使用图卷积网络对电站空间特征进行提取， 并根据提取的时空特征信息和历史数据来训练光伏发电预测模型。 文献[11]采用深度学习方法对光伏出力进行预测，预测结果表明，深度学习算法优于浅层学习算法。 文献[12] 提出了一种小波变换（Wavelet Transform）与神经网络相结合的预测算法，并利用该算法对光伏阵列的超短期功率进行了有效预测。 文献[13]在泛在电力物联网背景下，提出了一种基于Elman 网络的光伏出力预测模型，并采用智能算法对该预测模型的权值进行优化， 以提高预测精度。 文献[14]针对环境温度、环境湿度和太阳辐照度3 个因素， 建立基于云团变化的光伏短期发电功率预测模型和普适性的云规则生成器，利用主成分分析法对输入数据进行降维处理，并使用遗传算法对预测模型进行优化， 分析结果表明，该模型具有良好的预测能力。 文献[15]重点分析了光伏电站数据的质量， 并采用清洗方式对数据进行异常处理，此外，根据预测模型的成本约束和运行需求， 提出一种基于核函数极限学习机的分布式光伏发电功率预测方法。

在复杂的光伏电站运行环境下， 本文提出了一种基于数据清洗与组合学习的光伏发电功率预测方法。考虑到变电站实际运行时，通信与传输过程中的数据遗漏状况， 在数据输入模型前采用KNN 算法对缺失数据进行补全；然后，利用Lasso算法将极限学习机 （Extreme Learning Machine，ELM）、 神经网络模型和Adaboost 模型的预测结果进行动态组合，以获得最终预测结果；最后，采用北京大兴区的实际光伏发电数据来验证模拟结果的准确性。

1 预测模型及算法机理分析

1.1 基于KNN 算法的数据清洗方式

本文研究对象为光伏电站。 光伏电站一般处于配电网和电压等级较低的输电网中， 属于电力系统的末端环节， 该电压等级下的电网并不能如大电网一样做到精细化管理。 配电网和电压等级较低的输电网的通信和信息系统发展得相对滞后， 使得该电压等级下电力系统中测量误差和传输设备故障率均较高， 使得设备可靠性变差。 此外， 配电网中管理调度人员的数量和维修人员的专业素质也有待提高， 人为因素造成的数据质量不高的状况也应该得到高度重视。

光伏电站数据极易出现缺失， 如果不对缺失数据进行有效清洗， 直接将缺失数据嵌套入预测模型进行训练，对预测模型产生巨大影响，从而导致光伏出力预测的精度大幅度降低。 对于降压变电站的数据缺失问题，预测模型使用KNN 算法进行数据清洗，KNN 算法是缺失数据清洗中较为有效、计算复杂度较低的算法，在机器学习实际工程的数据预处理方面得到广泛应用，考虑到KNN 算法中欧式距离越近，数据间相似度越高这一情况，KNN 算法选取了数据集中与缺失数据最近邻的、最完整的k 个数据补全缺失值。KNN 算法模型的计算式为

式中：Yi为第i 个样本点的前m 维特征向量，Yj=（yi1，yi2，yi3，…，yir），其中，yir为第i 个样本点的第r维属性。

1.2 核函数极限学习机

ELM 属于单层前馈神经网络算法。ELM 输出函数f（x）的表达式为

式中：h（x）为隐藏层计算所得的输出；β为隐藏层与输出层之间的连接权重，β=[β1，…，βL]T。

核函数极限学习机的误差表达式为

式中：L 为神经元的数目；βi，hi（x）分别为第i 个节点的权值和输出值；fO（x）为真实标记值。

核函数极限学习机的基本架构如图1 所示。

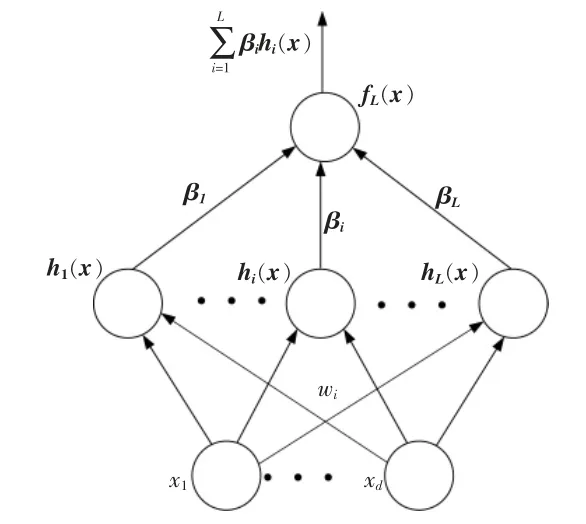
图1 核函数极限学习机的基本构架Fig.1 Kernel-based extreme learning machine

核函数极限学习机输出函数fL（x）的表达式为

式中：gi（x），G（ai，bi，x）均为第i 个隐藏节点的输出函数；ai，bi均为隐藏层参数。

训练前馈神经网络所需要权重的最优二乘解的表达式为

式中：T 为预测目标值；H 为神经网络隐藏层矩阵。

模型输出权重的最小标准二乘解表达式为

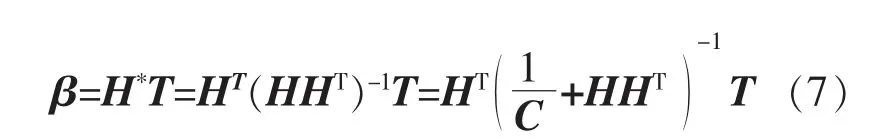
式中：H*为H 的广义逆矩阵；1/C 为常数。

式（7）中的1/C，能够使求解结果具有更好的泛化能力。

1.3 Adaboost 模型

Adaboost 模型为叠加集成模型， 它训练了多个弱拟合模型，然后将各个弱拟合模型组合起来，构成一个强预测模型。 其总体思路是对正确样本赋予较低权值，对错误样本赋予较高权值，通过不断加权组合，提高预测模型的性能。

Adaboost 模型的计算步骤如下。

①从样本中选取n 组训练数据， 设初始化数据的分布权值为Di（i）=1/n。

②在训练第t 个弱学习器时， 用训练数据训练决策树，从而得到误差之和et为Dl（i）。

③根据预测误差之和et计算弱学习模型的权重αt。 αt的计算式为

④根据弱学习器调整下一轮训练样本的权重，更新公式为

式中：Dt（i）为第t 轮的权值，i=1，2，…，n；yt为第t轮的学习器；Bt为第t 轮的归一化因子。

⑤训练T 轮以后， 得到T 组弱学习器f（gt，αtt）， 由T 组弱学习器组合可以得到一个强学习器h（x）。 h（x）的计算式为

1.4 Lasso 回归方法

Lasso 回归方法是基于正则化的线性回归分析方法， 主旨思想是在相关系数绝对值之和小于一个阈值的条件下，使得残差的平方和最小化。

普通线性模型的表达式为

式中：Y 为最终负荷的预测值；X为第一层模型的预测值，X=（X（1），X（2），X（3）），其中，X（1），X（2），X（3）分别为第一层模型中ELM 模型、Adaboost 模型和ANN 模 型 的 预 测 值；ε 为 随 机 误 差 项，ε=(ε1，ε2，..，εn)；r 为回归系数。

Lasso 回归方法估计的表达式为

在模型训练过程中须要求解权重， 当权值计算完成后，表明负荷预测模型已建立完成。

2 基于数据清洗与组合学习的光伏发电功率预测模型

本文预测模型的建立过程包括数据清洗、模型训练和预测指标等过程。在数据的预处理阶段，数据清洗是整个数据分析过程中不可缺少的一环，也是较易被忽视的一环，以往的文献并没有对其足够重视， 数据清洗的质量直接决定了模型预测效果。在实际工程应用中，数据清洗时间往往占分析过程的50%～80%。由各电压等级光伏电站的实际情况可知， 低电压等级光伏电站的管理水平较低，相对来说，数据缺失的概率较高。因此，须要在数据输入模型前充分对数据进行清洗。 本文选取了光伏输入相关特征，输入数据包括总辐射S、组件温度Td、环境温度To、气压A、相对湿度H 和历史光伏发电功率P 进行数据清洗[12]。

单个模型容易陷入局部最小值， 且统计假设空间有限， 本文采用的模型组合可以提高预测算法的可靠性。 对于ELM 模型、Adaboost 模型和ANN 模型的预测结果， 采用Lasso 线性组合的方式进行学习。 为了确保Lasso 算法中各参数的实时性， 本文采用动态更新的方式改变Lasso 算法中的各个参数， 从而获得时序滚动的光伏预测模型，保证当前模型与数据的相互匹配。图2 为时序滚动的光伏功率预测模式。

图2 时序滚动的光伏功率预测模式Fig.2 PV output forecasting time horizon-rolling

本文模型的训练流程：首先，采用KNN 算法对缺失数据进行填充， 将填充后数据输入到ANN模型、Adaboost 模型和ELM 模型中，并分别对这3个模型进行训练； 为了避免ANN 模型和ELM 模型计算结果不确定性的影响， 本文以多组不同的参数值对ANN 模型和ELM 模型进行初始化，并从多个不同的初始点开始探索， 从而有效避免陷入不同的局部极小值， 然后获得更接近全局最小的结果；最后，将各模型的预测结果输入Lasso 线性模型，得到最终的光伏功率预测结果。基于数据清洗与模型组合的光伏功率预测方法的计算流程图如3 所示。

图3 基于数据清洗与模型组合的光伏功率预测方法流程图Fig.3 PV output forecasting based on data cleansing and model aggregation

3 算例分析

本文选用北京大兴区的光伏发电系统实际运行数据对模拟结果进行验证。 光伏发电系统总装机容量分别为400 kW，4 MW， 选取2017 年数据为训练数据，2018 年1 月份数据为测试数据。

本文的误差指标主要包括均方根误差（Root Mean Square Error，RMSE） 和标准化平均相对误差（Normalized Mean Absolute Error，nMAE）。

RMSE，nMAE 的表达式分别为

式中：fi，ti分别为i 时刻光伏发电系统的实际发电功率和预测发电功率；tm为最大装机容量。

3.1 数据预处理方案对比

为了分析不同数据填充方案的优劣，将KNN补全算法、 线性插值的补全方法和不使用补全算法的计算结果进行对比。在相同的模型架构下，分别采用3 种方式对模型进行训练。

不同数据补全算法对预测结果影响见表1。

表1 不同数据清洗算法对预测结果的影响Table 1 Effect of different data cleansing algorithm

由表1 可知，电压等级越低、额定容量越小的光伏电站，数据缺失的情况越严重，这表明光伏电站的管理水平与电压等级具有相关性， 即电压等级越低、 额定容量越小的光伏电站的管理水平越低。 不同类型的光伏电站预测功率呈现不同的误差分布。此外，不使用补全算法对预测精度影响很大， 这是由于删除缺失数据的信息破坏了数据原有的内部特征，使得预测精度大幅度降低。采用线性插值方法时， 只能考虑输入数据中单一特征变量的存量数据结构， 对于缺失数据也只是简单的采用线性方法进行补全，因此，线性插值方法预测精度的提升幅度有限。利用KNN 补全算法对缺失数据进行填充，能够较好地还原数据初始形态，使得预测结果的精度较高。

3.2 预测效果对比分析

Lasso 算法动态地学习了各个模型的权重。因此，须要分析各个子模型对应权值的趋势。图4 为Lasso 模型权值随时间的变化情况，图中：β1，β2，β3分别为ELM 模型，Adaboost 模型和ANN 模型的权值。

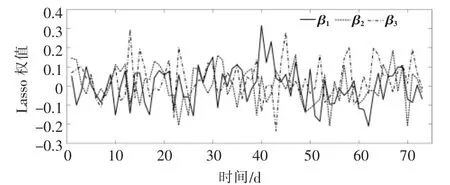
图4 Lasso 模型权值随时间变化情况Fig.4 Time-varying weights of Lasso model

由图4 可知，Lasso 模型在不同时段通过计算获得不同模型的权值， 说明在当前预测场景条件下， 各模型具有不同的优势，Lasso 算法能够充分学习到各个子模型的优点， 使得预测效果得到进一步提升。

天气情况对光伏输出功率影响较大。因此，为了进一步验证本文算法的准确性和优越性， 分别在晴天和阴天的场景下， 对组合学习模型和单模型（ANN）的预测结果进行分析。 图5 为不同天气条件下， 额定输出功率分别为400 kW，4 MW 的光伏发电系统输出功率的预测结果随时间的变化情况。

图5 不同天气条件下，不同额定输出功率光伏发电系统输出功率的预测结果随时间的变化情况Fig.5 PV power output forecasting under different weather conditions as time change with different rated power

将本文组合学习预测模型的预测结果与SVM 模型[6]、ANN 模型[7]和时间序列算法[8]的预测结果进行比较。 其中，ANN 模型的内置节点分别为14，100，1；SVM 模型核函数参数为径向基函数，惩罚系数为1 000，核函数系数为10-3。各个算法的预测结果如表2 所示。

表2 不同场景下多个模型的光伏预测误差Table 2 Photovoltaic forecasting error of several models

由表2 和图5 可知，与阴雨天气相比，晴朗天气下各个模型的预测精度较高， 这是因为晴朗天气下光伏出力的变化较为平稳， 导致光伏出力的变化曲线较为平滑。此外，在阴雨天气下各个模型的预测误差普遍偏大， 这是由于云层与太阳辐照度的变化使得光伏出力产生突变。 对于模型的预测效果而言，相较于其他模型，组合学习模型的计算结果能更好地显示出光伏出力的变化趋势。 在多个光伏预测的场景下， 本文模型均获得了最高的精度和泛化能力， 这是因为本文组合模型聚合了多种学习算法， 并将其动态结合以提高本文模型的泛化性和鲁棒性。对其他算法而言，神经网络只使用了单一学习方法，容易陷入局部极小值，使得整体泛化性不高。 支持向量机输入数据挖掘的信息有限，虽然该算法也有较高的预测精度，但仍低于本文的预测方法。 时间序列算法的学习能力较弱， 只能计及光伏的历史信息， 预测精度也偏低。由此可见，本文使用的组合预测模型对于电力系统制定合理的运行策略有着较高参考价值。

4 结论

本文提出一种基于数据清洗与组合学习的光伏发电功率预测方法。 考虑到变电站实际运行中通信和传输过程中的数据遗漏情况， 在数据输入模型前采用KNN 算法对缺失数据和异常数据进行清洗，然后，通过Lasso 算法将ELM 模型、ANN模型和Adaboost 模型的预测结果进行动态组合。模拟结果表明：利用KNN 算法能够良好地清洗光伏发电站中的缺失数据和异常数据， 使得整体数据能够恢复到原有特征； 组合学习方式能够充分发挥多种算法的优势， 针对不同容量的光伏电站均有良好的预测结果； 晴天条件下， 本文模型的RMSE相较于神经网络、 支持向量机和时间序列分别提高了1.22%，1.83%，2.99%，阴雨天条件下，本文模型的RMSE 分别提高了0.66%，1.78%，4.68%。

目前，本文模型主要围绕点预测展开，概率预测与组合学习方式的结合仍然有待于深入挖掘，数据的填充方式只考虑了同一尺度数据的相互关系，对于历史数据的变化趋势仍值得深入分析。