不同坡膛锥度对弹丸挤进过程影响仿真研究

何 行，彭松江，邱群先，宋海通，贺旭光

(中国船舶集团公司第七一三研究所， 郑州 450015)

在一次膛炸故障中，弹药厂家认为，由于该火炮身管的坡膛锥度小，膛线起始部磨损后坡膛锥度变更小，造成了弹丸嵌膛瞬间的冲击超过了炸药稳定极限，在膛内发生异常爆炸。针对该问题争论，本文开展不同坡膛锥度条件下，弹丸挤进坡膛过程中弹体受力的分析研究。

弹丸挤进坡膛过程是一个极其复杂的非线性力学过程，涉及到弹带材料塑性变形、弹丸直线运动加上自身旋转耦合作用、以及接触面复杂受力，且行程和时间非常短，难以试验直接测量观测研究，因此经典内弹道学将其简化处理，基于瞬时挤进等基本假设，能够较好的指导火炮工程实践。“瞬间挤进”假设认为，在达到挤进压力的瞬间，弹丸才开始运动，简化并忽略了弹丸启动，弹带挤进膛线的过程，直接以30～40 MPa挤进压力作为内弹道的启动条件，简化了弹丸克服拨弹力后挤入膛线前这段运动。“瞬间挤进”假设已经无法满足研究弹带挤进过程的需要。

目前针对弹丸挤进过程的研究已经不少，文献[1]通过建立弹带挤进坡膛的有限元模型，研究了弹丸动态挤进阻力和弹丸运动规律的研究，但未深入到坡膛受力的研究。文献[2]考虑弹炮热力耦合的有限元模型，并计及了拨弹力，研究了影响弹带挤进过程和随后内弹道过程的因素，但没有考虑坡膛结构变化的影响。文献[3-4]通过数值计算研究了坡膛结构变化对弹丸挤进力和内弹道变化和坡膛受力的影响。文献[5-6]通过建立有限元模型，研究了枪械射击过程中，不同坡膛锥度对挤进过程坡膛处受力规律，并获得了满足弹头初始条件的坡膛锥度取值。文献[7]通过试验、理论和建立弹头挤进过程的有限元模型，研究了多组坡膛锥锥度与挤进力间的关系以及揭示了狙击步枪挤进力的形成机理。文献[8]以某钢心3层结构弹丸挤进过程为研究对象，得到了弹丸挤进阻力变化规律，分析了弹丸的应力、转速和挤进过程中的摆动情况。文献[9]研究了同一种坡膛结构下，弹丸连续冲击坡膛，膛线起始部位坡膛的受力规律，对于研究身管寿命具有重要的意义。

本文是针对弹药厂家提出的由于火炮坡膛锥度小(磨损后锥度更小)，导致弹丸挤进坡膛过程中弹体受力大，是造成膛炸的主要原因的观点，提出质疑，采用基于Johnson-cook塑性本构模型，建立了弹炮耦合动力学非线性有限元模型，利用ABAQUS/Explicit求解技术，研究了弹丸挤进过程复杂的塑性变形下的受力过程，得到了弹体受力、弹丸速度与炮口振动等仿真计算结果，分析了不同坡膛锥度对弹丸挤进过程受力环境影响的变化规律。

1 弹炮耦合有限元计算模型

1.1 有限元模型

为了保证有限元计算精度，严格按照实物的尺寸和装配关系，在PTC/Creon软件中分别建立身管、膛线、弹丸、弹带的实体模型后，导入到Hypermesh软件中划分好网格，然后导入到ABAQUS软件中，使用C3D8R网格单元，具有膛线结构的身管和具有弹带结构的弹丸合膛有限元模型如图1所示。

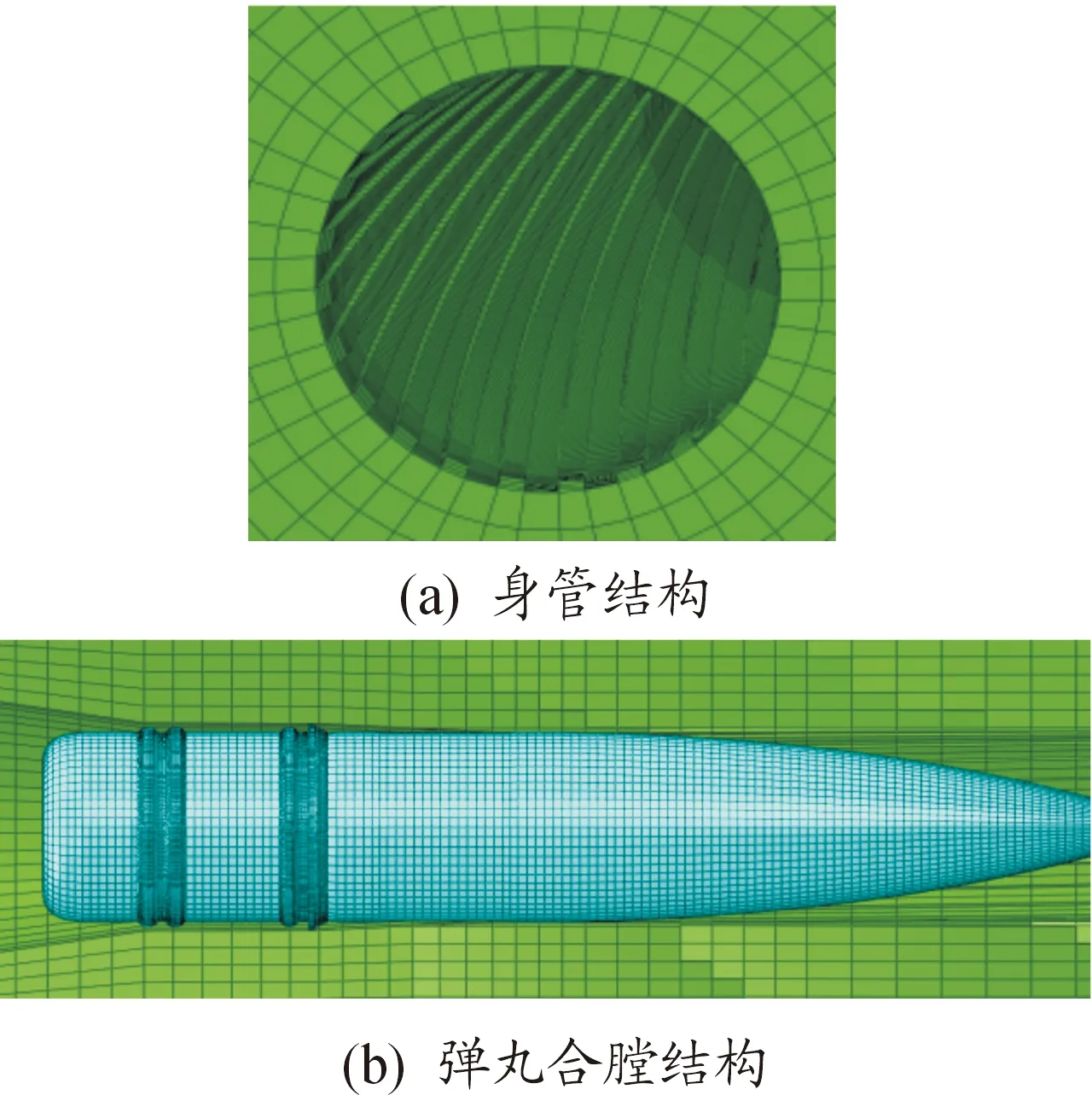
图1 身管、弹丸合膛结构有限元模型

1.2 材料模型

弹带材料为黄铜，身管材料为炮钢。弹丸在挤进过程中经历弹塑性变形及损伤，最终发生局部化韧性断裂，涉及弹带材料的应变硬化、应变率硬化和温度软化，因此采用Johnson-Cook塑性及其断裂失效模型。身管由于承受火药气体和弹带的连续瞬时冲击，采用Johnson-Cook塑性本构模型。计算模型的理论公式如下：

(1)

(2)

(3)

1.3 加载方法

本文研究的是简化模型，重力载荷作为常力加载，故只约束身管尾端面3个方向自由度，将试验测试的弹底压力-时间曲线(图2)，插值处理为函数施加在弹丸底部的作用面上，来模拟火药气体对弹丸的作用。前、后弹带和装药分别与弹体使用绑定(Tie)约束关系，使其固定在弹体上，身管与炮尾固定约束，如图3所示。

为研究不同坡膛锥度弹带挤进过程对弹体受力的影响，在相同条件(身管建模、载荷施加、边界条件和网格属性等相同)下，分析对比弹丸在膛内运动特性。本模型仅限于弹丸挤进坡膛过程中坡膛受力规律的研究，不考虑弹后气体压力和温度变化对受力的影响。

图2 加载压力曲线

图3 身管、弹丸及弹带有限元加载模型

1.4 计算条件

为了对比不同坡膛锥度条件下，坡膛挤进过程对弹丸弹体的受力影响，不改变药室结构，将坡膛起始点位置固定，改变坡膛锥度。以现火炮1/24.6的坡膛锥度为基础，假设了坡膛锥度由小到大变化，共7种计算条件。坡膛坡度和坡膛长度的对应关系如表1所示。

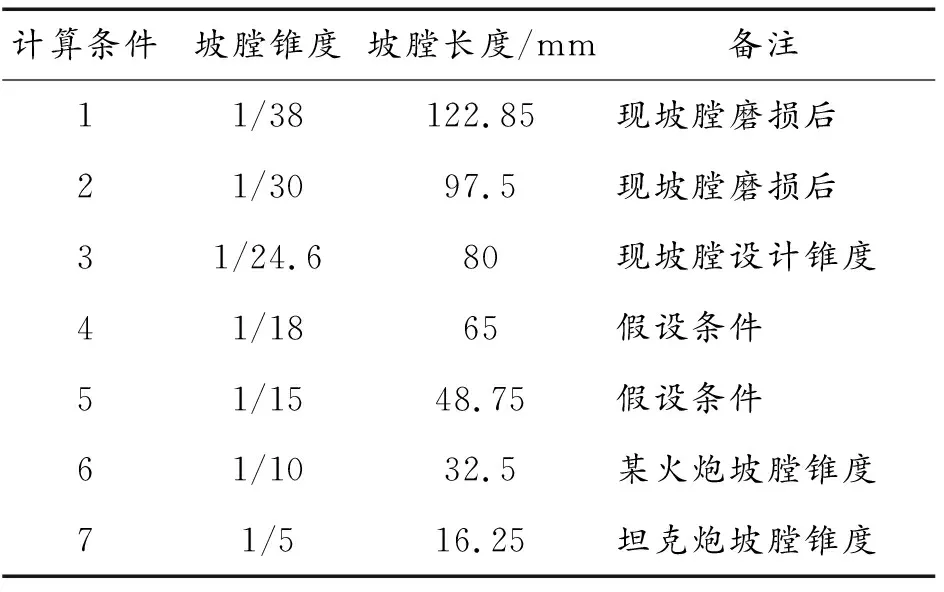
表1 计算条件参数

2 弹丸挤进过程数值计算结果与分析

2.1 现1/24.6坡膛锥度的计算结果

首先以现坡膛锥度为计算条件，验证计算模型的正确性,研究当前条件发射过程中弹丸受力情况，进行了全内弹道过程仿真计算，分别提取弹丸在膛内运动过程中的弹体前弹带处受合力、轴向剪切力和径向剪切力随时间变化曲线，分别见图4、图5和图6所示。

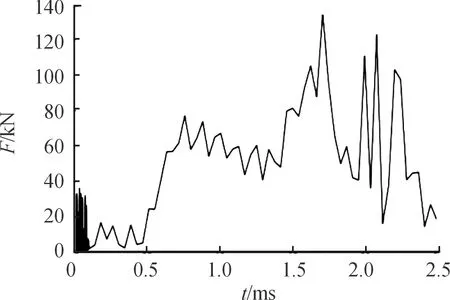
图4 弹体前弹带处受合力曲线

图5 弹体前弹带处受剪切力曲线(轴向)

图6 弹体前弹带处受挤压力曲线(径向)

从图4、图5和图6的计算结果曲线结果分析：

在0.5 ms时凸缘弹带接触坡膛壁弹体受力幅值大约为整个挤进过程弹体受力最大幅值的1/3，并无明显的冲击现象，同时证明了凸缘弹带的重要作用，有效加大挤进初期的弹带强制量，减小对火炮身管膛线起始部磨损的敏感性，提高磨损后密闭火药气体的能力。

从图4弹体前弹带处受剪切力(轴向)和图5弹体前弹带处受合力的曲线来看，2个曲线力的方向相反，幅值及变化趋势接近，所以弹丸在挤进膛线过程中，轴向剪切力对弹体受力作用非常显著，径向挤压力作用较小。

2.2 现1/24.6坡膛锥度和1/5坡膛锥度仿真计算结果对比与分析

为研究坡膛锥度变大后弹丸挤进膛线过程中弹体受力变化规律，建立坡膛锥度为1/5的炮身弹炮耦合有限元模型进行分析计算，截取与现火炮1/24.6坡膛锥度条件下弹丸运动过程中的典型同一时刻的弹体受力云图汇总，见表2所示。

第一，尽快研究制定《合作社法》，确立合作社必须坚持的基本原则，包容上述各种合作社类型。目前，农机合作社、土地股份合作社都在工商管理部门注册，农村社区股份合作社有的在工商部门注册，有的在农业行政管理部门注册，前者注册为合作社法人，后者则不具备经营职能。这种情况说明，目前的《农民专业合作社法》无法容纳实践中出现的合作社类型，不能满足广大农民发展合作经济的需要，必须制定一部统一的《合作社法》，对上述各类合作社的运作规则进行具体规定。

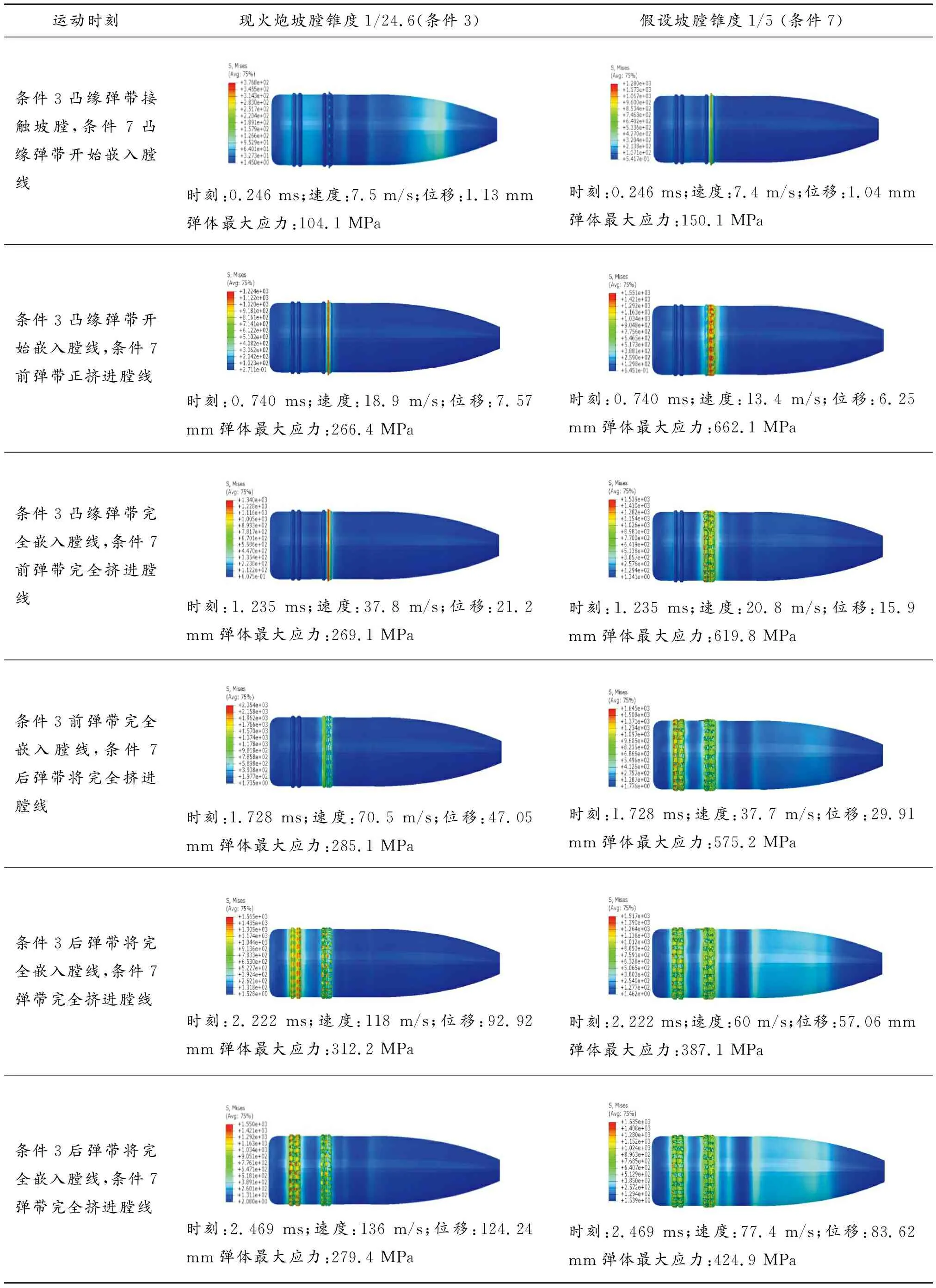
表2 两种典型坡膛锥度条件下的仿真结果云图

从表2中的1/24.6坡膛锥度和1/5坡膛锥度弹体受力云图可以看出：

在弹丸挤进坡膛过程中，二者相比，坡膛锥度大，弹体弹带挤进膛线时机早，弹丸运动速度慢；

坡膛锥度较大时，弹带嵌入膛线过程中，弹体最大应力明显较大。

2.3 不同坡膛锥度条件数值计算结果与分析

为进一步研究不同坡膛锥度条件下弹体受力情况，增加计算样本量，提取7种不同坡膛锥度工况下，仿真过程弹带挤进过程中，弹体前弹带处的最大合力、最大剪切力、最大应力、挤进过程结束时弹体最大速度、炮口振动最大位移，将上述数据汇总如表3所示。

为进一步分析，将表3中的弹体的最大合力和最大轴线剪切力、挤进过程结束时弹体速度、挤进过程结束时炮口振动随坡膛锥度变化进行数值分析。分别如图7、图8、图9所示。

图7 挤进过程弹体最大受力随坡膛锥度变化曲线

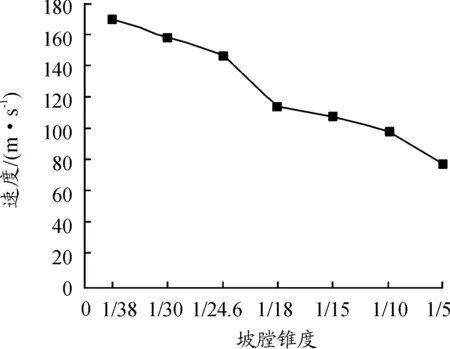
图8 挤进完成时刻弹体运动速度随坡膛锥度变化曲线

图9 挤进完成时刻炮口振动最大位移随坡膛锥度变化曲线

通过图7、图8、图9的曲线可以看出：

其他不变的条件下，改变坡膛锥度，随着坡膛锥度减小，弹带挤进过程中弹体最大受力减小：相比设计坡膛锥度1/24.8，坡膛锥度为1/38和1/30时，相当于磨损后工况，弹体最大受力分别减小了38%和15%，当坡膛锥度增加到 1/5，弹体最大受力增大了3.6倍。

随着坡膛锥度的变大，弹丸前进阻力变大，对炮身的反作用力变大，因此炮口振动位移变大。相比设计坡膛锥度 1/24.8，当坡膛锥度为1/38和1/30时，相当于磨损后工况，炮口振动最大位移分别减小了18%和10%，当坡膛锥度增加到1/5，炮口振动最大位移增大了1.14倍。

3 结论

1) 某火炮坡膛锥度小，弹带挤进膛线过程中，弹体受力为135 392 N；坡膛锥度变大时，弹体受力会急剧增大；

2) 仿真弹带挤进膛线的运动过程显示，挤进过程无明显的冲击现象；

3) 坡膛磨损后，相当于坡膛锥度变小，弹体最大受力降低，因此某火炮坡膛锥度小和磨损后锥度变小不是造成膛炸的原因。

4) 同一计算环境下，仿真结果数值可以反映分析不同坡膛锥度条件下的弹带挤进过程弹体受力变化趋势和规律。在归零射击试验中，使用坡膛磨损接近寿命极限，比事故身管磨损更加严重的身管，发射与故障是所用同一批次弹药数百发，故障未复现，间接证明了仿真结论的正确性。

5) 本文基于简化模型，按试验获得的弹底压力-时间曲线将压力施加在弹丸底部的作用面上；研究工作仅探讨了弹丸冲击坡膛过程的综合性能规律，没有考虑火药气体和温度对坡膛的影响，将在下一步工作中继续展开研究。