对回旋加速器模型的深度剖

◇ 安徽 乔 军 方 林

回旋加速器是利用相互正交的电磁场使带电粒子在电场中加速,在磁场中回旋,通过多次往复最终使粒子得到加速的装置.它是带电粒子在组合场中运动的重要实例,也是现代科技在物理中的重要应用,是高考考查的重点和热点问题.本文对回旋加速器模型进行深度剖析,对涉及的重要规律和疑难问题进行全面梳理和总结,以供师生参考.

以下讨论均不计粒子注入时的初速度,粒子最终离开加速器的速度远小于光速.

问题1 粒子注入初始位置在哪儿?

因被加速的粒子在运动过程中会经高频电场反复多次加速,每加速一次后紧接着在磁场中做半周匀速圆周运动,然后不断重复这一过程,直至粒子最终离开D形盒,故粒子刚开始注入位置应该在D形盒的中心位置附近,而并非D形盒边缘(道理很简单,如在边缘注入,粒子加速后半径再次增大,就会撞到D形盒上).

问题2 回旋加速器实现的条件与交变电场的变化周期是什么?

高频电场加在两D形盒之间,由于D形金属盒的静电屏蔽作用,盒内空间的电场极弱,故带电粒子在盒内仅受洛伦兹力作用而做匀速圆周运动.因粒子做匀速圆周运动的周期与运动速率和半径均无关,所以尽管粒子的速率和半径一次次增大,运动周期T却始终不变.如图1所示,如果在直线AB、A′B′间加上一交变电场,使之以相同的周期变化,就可以保证粒子每经过直线AB和A′B′时都正好赶上适合的电场方向(电场力方向与速度方向相同)而被继续加速(不考虑加速时间).

图1

然而,一方面,由于D形盒所占空间有限,另一方面,随着粒子速度的增加,当其接近光速时,由狭义相对论可知,粒子的质量会明显增加,回旋周期T＝会变大,与交变电压的周期不再一致,也就无法保证粒子每次出磁场后就立即被加速,从而导致加速器无法正常工作,因此回旋加速器不能无限地对带电粒子加速.

问题3 最大动能是多少?

设粒子从D形盒边缘离开时做圆周运动的轨迹半径为rm,D形盒半径为R,速度为vm,则rm＝R,粒子做匀速圆周运动,由洛伦兹力提供向心力,有则粒子获得的最大动能

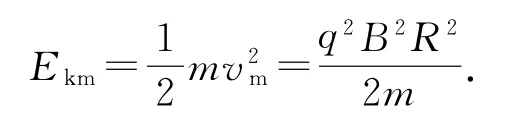
即对于某一粒子,其最大动能取决于D形盒的半径R及磁感应强度B,与加速电压无关.当然,最大动能是要靠电场的多次加速才获得的,因为洛伦兹力永不做功.

问题4 可以同时加速不同粒子吗?

问题5 粒子的运动时间怎么求?

带电粒子在回旋加速器中经过多次加速和匀速圆周运动.设粒子在磁场中的加速次数为n,加速电压为U.因每加速一次粒子获得的能量为qU,且加速一次就会接着回旋半周,即在每个周期内,带电粒子两次进入D形盒的缝隙间被加速两次.结合Ekm＝故带电粒子在磁场中做匀速圆周运动的时间

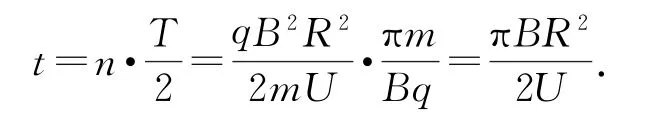
虽然粒子的加速运动与圆周运动是间隔开来的,但只要剔除圆周运动,粒子的加速运动就是一个连续的匀加速运动了(等效看作同一直线上的加速运动),则粒子在狭缝中经n次加速的总时间由牛顿第二定律有,故电场对粒子加速的时间

换一种思路求两种时间.

因粒子经n次加速的位移大小为nd,在电场中加速的总时间为而粒子在D形盒中做匀速圆周运动的周期不变,且最后半周的时间则圆周运动的总时间即当R≫d时,电场加速时间可以忽略不计,故求粒子在回旋加速器中运动的总时间,通常仅考虑在磁场中的匀速圆周运动时间.

问题6 回旋半径怎样变化?

粒子被加速一次所增加的动能为qU,粒子被n次和n＋1次加速后的动能分别为

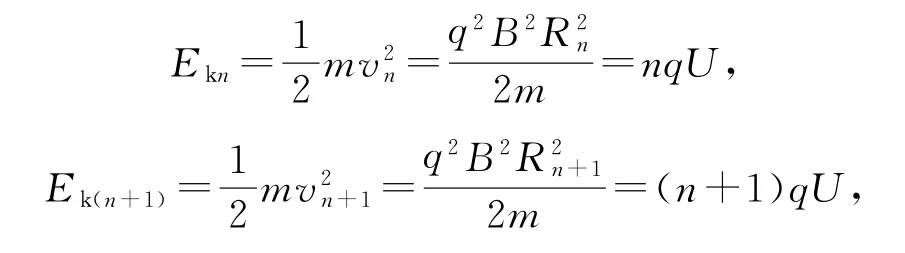
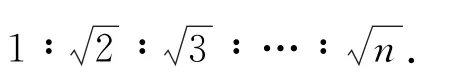
例11930年劳伦斯制成了世界上第一台回旋加速器,其原理如图2所示,这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,下列说法正确的是( ).

A.离子由加速器的中心附近进入加速器

图2

B.离子由加速器的边缘进入加速器

C.离子从磁场中获得能量

D.离子从电场中获得能量

解析

根据回旋加速器的原理可知,离子由加速器的中心附近进入加速器,A正确,B错误;离子从电场中获得能量,C错误,D正确.

点评

题中离子每次加速进入磁场中,轨道半径会较上半圈变大,如果注入位置在边缘,则加速一次或几次就会撞到回旋加速器上.另一方面,只要抓住洛伦兹力永不做功的特点,即可明白离子的动能必然是通过电场加速而来的.值得一提的是,教材中的插图和“问题与练习”“做一做”“思考与讨论”等易忽视之处均可能成为高考命题的素材,应引起大家注意.如教材中给出了回旋加速器工作原理示意图,细心的同学会注意到图中粒子注入的位置在加速器中心位置附近.

例2图3-甲为EarnestO.Lawrence设计的回旋加速器的示意图.它由两个铝制D形金属扁盒组成,两个D形盒正中间开有一条狭缝;两个D形盒处在匀强磁场中并接有高频交变电压.图3-乙为俯视图,在D形盒上半面中心S处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D形盒中.在磁场力的作用下运动半周,再经狭缝电压加速;为保证粒子每次经过狭缝都被加速,应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致.如此周而复始,最后到达D形盒的边缘,获得最大速度后被束流提取装置提取出.已知正离子的电荷量为q,质量为m,加速时电极间电压大小恒为U,磁场的磁感应强度为B,D形盒的半径为R,狭缝之间的距离为d.设正离子从离子源出发时的初速度为零.

(1)试计算上述正离子从离子源出发被第一次加速后进入下半盒中运动的轨道半径.

(2)尽管粒子在狭缝中每次加速的时间很短但也不可忽略.试计算上述正离子在某次加速过程中从离开离子源到第n次被加速结束时所经历的时间.

(3)不考虑相对论效应,试分析要提高某一离子被半径为R的回旋加速器加速后的最大动能可采用的措施.

图3

解析

(1)设正离子经过窄缝被第一次加速后的速度为v1,由动能定理得,正离子在磁场中做匀速圆周运动,半径为r1,由牛顿第二定律得由以上两式解得.

(2)设正离子经过窄缝第n次被加速后的速度为vn,由动能定理得粒子在狭缝中经n次加速的总时间由牛顿第二定律得ma,解得电场对粒子加速的时间.

点评

本题中第(1)问很常规,只需采取离子在组合场中运动的处理思路——分段研究,抓住衔接点的速度即可求解,即先根据前文分析,对离子分别列出牛顿运动定律或动能定理,再根据前文分析列出在磁场中运动的半径方程,然后消去速度便可得出半径的大小.第(3)问突破难点的关键在于抓住最大动能的离子对应半径应等于D形盒半径,再由动能表达式求出即可,这也是回旋加速器问题常考的一个知识点.而第(2)问可以直接运用问题5的分析方法,即将离子每次在磁场中的时间求出来(为便于找出通项,一般要求出前3次的时间),然后再累加求和.要注意的是,本题要求解的是从离开离子源到第n次被加速结束时所经历的时间而非最终引出D形盒的时间(第n次加速后,并不一定获得最大速度).此外,本题强调不可忽略电场中的加速时间,计算总时间时必须考虑.

例3回旋加速器的原理如图4所示,D1和D2是两个中空的半径为R的半圆金属盒,它们接在电压一定的交流电源上,位于D1圆心处的粒子源A能不断产生粒子(初速度可以忽略,重力不计),它们在两盒之间被电场加速,粒子的比荷为置于与盒面垂直的磁感应强度为B的匀强磁场中.

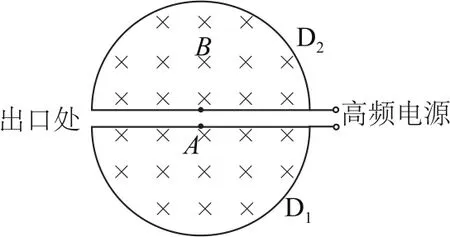
图4

试推理说明:粒子在回旋加速器中运动时随着轨道半径r的增大,同一盒中相邻轨道的半径之差Δr是增大、减小还是不变?

解析

设k(k∈N∗)为同一盒子中粒子运动轨道半径的序数,相邻的轨道半径分别为rk,rk＋1(rk＜rk＋1),Δrk＝rk＋1－rk,在相应轨道上粒子对应的速度大小分别为vk,vk＋1,D1、D2之间的电压为U.

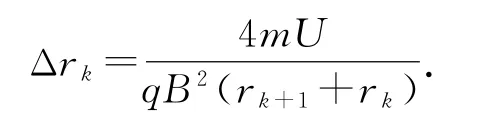
因U、q、m、B均为定值,令由上式得,相邻轨道半径rk＋1,rk＋2之差

点评

求解本题的关键之处在于找到相邻轨道的半径之差Δr的变化规律,而相邻轨道的半径大小又跟粒子的运动速度有关,可以通过研究粒子的加速次数,再根据动能定理求出.因此,我们可以在问题6的基础上,因洛伦兹力不做功,且每加速一次电场力做功相同,均为qU,由此求出每次进磁场时的初速度,进一步将Δr的通项表示出来,然后利用数学知识判断Δr的大小变化情况.根据问题6的分析,还可推知相邻轨道的间距按规律变化,由此可知,随着加速次数的增加,相邻轨道的间距会不断缩小,而并非等距变化.

图5

变式同步加速器在粒子物理研究中有重要的应用,其基本原理可简化为如图5所示的模型.M、N为两块中心开有小孔的平行金属板,质量为m、电荷量为＋q的粒子A(不计重力)从M板小孔飘入板间,初速度可视为零.每当A进入板间,两板的电势差变为U,粒子得到加速,当A离开N板时,两板的电荷量均立即变为零.两板外部存在垂直纸面向里的匀强磁场,A在磁场作用下做半径为R的圆周运动,R远大于板间距离.A经电场多次加速,动能不断增大,为使R保持不变,磁场必须相应地变化.不计粒子加速时间及其做圆周运动产生的电磁辐射,不考虑磁场变化对粒子速度的影响及相对论效应.求:

(1)A运动第1周时磁场的磁感应强度B1的大小;

(2)粒子绕行n周所需总时间tn;

(3)在A运动第n周的时间内电场力做功的平均功率

解析

(1)设A经电场第1次加速后速度为v1,由动能定理得

A在磁场中做匀速圆周运动,所受洛伦兹力充当向心力,有

由式①②得

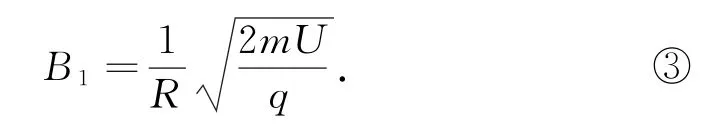
(2)粒子做半径为R的匀速圆周运动,每一周所用时间为.

由于每一周速度不同,所以每一周所需时间也不同.

由此可以推知,第n周的速度.

故绕行n周所需总时间

(3)设A经n次加速后的速度为vn,由动能定理得

设粒子做第n次圆周运动的周期为Tn,有

设在A运动第n周的时间内电场力做功为Wn,则

在该段时间内电场力做功的平均功率为

点评

变式题中的加速器模型与常见的回旋加速器的最大区别在于保障了粒子的回旋半径不变,这也是解决本题的关键之处.两题情境相似之处是:磁场(洛伦兹力)改变粒子的速度方向,电场(电场力)改变粒子速度.因为不计粒子的加速时间,所以将每周的圆周运动时间加起来即为总时间,这一点与问题5的分析思路相同.从知识结构来看,变式题与原题均考查带电粒子在复合场中的运动,解决问题需要分段分析电场与磁场中的两类典型运动,分析电场中的加速运动时仍可以将其等效为连续的匀加速运动.而变式题中由于R不变,则粒子每周回旋的时间会随加速次数的增大而减小,因此不能用第一周的时间乘加速次数来求总时间,这也是易错之处.之所以作如此变化,是给学生一定警示:看到熟悉情境,不进行具体问题具体分析,而只知道硬套照搬规律结论,就会因思维定式而出错.将变式题与原题进行对比分析,可以起到拓宽学生视野、破除定式思维的作用.

综上,分析回旋加速器问题,需要我们掌握其工作原理,理解一些重要特点,灵活运用一些重要推论,抓住分析该类问题的几个关键点:分段处理(方法)、衔接速度(联系)、周期性.