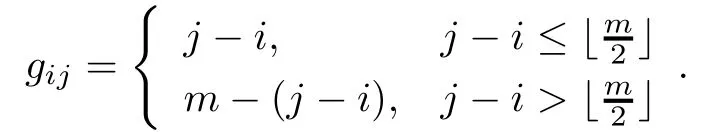单圈图(外围)Wiener指标的计算公式

李建喜, 雷思宇

(闽南师范大学数学与统计学院,福建漳州363000)

§1 引 言

设G=(V,E)为具有n个顶点的简单连通图,对于任意顶点u,v∈V(G),两点间的距离d(u,v)为u和v之间的最短路径长度,还可记为dG(u,v).对v∈V(G),顶点v的离心率ε(v)=max{d(u,v)|u∈V(G)},图G的直径d(G)=max{ε(v)|v∈V(G)}.外围顶点集P(G)指图中满足ε(v)=d(G)的顶点的集合.用dG(x)记为在G中顶点x到其余顶点的距离和,即.用W(G)表示图G的Wiener指标,PW(G)表示图G的外围Wiener指标.对于图G中的割边e∈E(G),分别用n1(e),n2(e)表示G中分布在边e两侧的顶点数目,p1(e),p2(e)分别表示G中分布在边e两侧的外围顶点数目;若e∈E(G)且边e不为G的割边时,规定分布在边e两侧的顶点数目分别为0.用|G|表示图G中顶点的数目.顶点数目和边数目相同的简单连通图称为单圈图.

图的Wiener指标是由著名的化学家Wiener在1947年首次提出的基于距离不变量的一种拓扑指标,其与图的结构性质之间有着密切的联系,相关结果和进展可参见文献[1-4].图G的Wiener指标在文献[1]被定义为图中所有不同顶点对间的距离之和,即

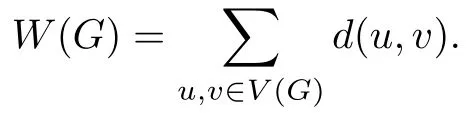
而外围Wiener指标是Wiener指标的一部分,是2017年由K.P.Narayankar和S.B.Lokesh在文献[5]中在Wiener指标的基础上首次提出.其定义为图G中所有不同外围顶点对间的距离之和,即

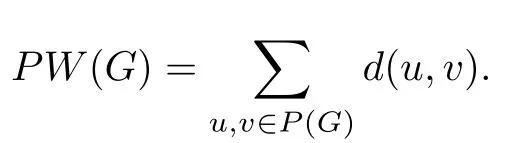
文献[6]研究了简单连通图的Wiener指标和外围Wiener指标的差的上界和下界;文献[7]主要探究了树图的外围Wiener指标,得到了树图外围Wiener指标的上界和下界,还有当给定外围顶点数目和直径时树图的外围Wiener指标的上界和下界.在文献[7]中求树图的外围Wiener指标的上下界时用得更多的公式不是定义式,而是求和每条边对Wiener指标贡献的一个式子,一条边对Wiener指标的贡献是指在这条边的一侧的所有顶点到另外一侧的所有顶点的距离之和中,该条边被经过的次数.因为树图中任意边都是割边,所以其贡献为分布在其两侧的顶点数目的乘积,即

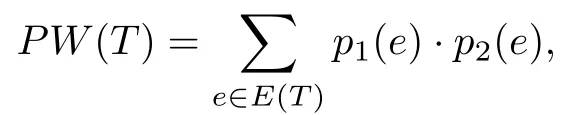
这个式子是由文献[1]中树图的Wiener指标的计算公式

而导出的.

文献[8]给出了一个关于单圈图Wiener指标的计算公式,且刻画出了最大,最小,次大,次小,第三大,第三小的Wiener指标的单圈图的特征.这个公式主要是通过对顶点的分类而得到的,其形式较为复杂,且没有获得相应外围Wiener指标的计算公式.本文将通过将单圈图的边分成两类(圈上的边和不在圈上的边),分别考察这两类边对其Wiener指标的贡献,从而得到一个形式相对简洁的单圈图的Wiener指标的计算公式,同时也获得单圈图的外围Wiener指标的计算公式.其形式类似于树图上的(外围)Wiener指标的计算公式.

§2 主要结论

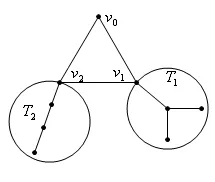
在给出新的单圈图的Wiener指标计算公式之前,首先回顾一下文献[8]中的关于单圈图的Wiener指标计算公式,设G为具有n个顶点单圈图,其所含的圈记为Cm=v0v1···vm−1v0.设T1,T2,···,Tk(1≤k≤m)为G−E(Cm)中的非平凡分支,其中V(Ti)∩V(Cm)=ui,i=1,2,···,k.令|Ti|=li+1,wi=dTi(ui),w=dCm(u),u∈V(Cm),其中i=1,2,···,k.则单圈图G的Wiener指标可表示为

图1 单圈图Un

证对于单圈图Un的Wiener指标,可将其边分为不在圈上的边和在圈上的边两类,然后分别算出这两类边对其外围Wiener指标的贡献,进而求和来获得.

对于e∈E(Un),若eE(Cm),则显然e为Un的割边,这时边e对W(Un)的贡献是在其边e的一侧的所有顶点到其另外一侧所有的顶点的距离之和中,e被经过的次数,即这条边两侧顶点数目的乘积.将所有这些边对W(Un)的贡献记为W1(Un);若e∈E(Cm),则显然e不为Un的割边,由规定可知,其边两侧顶点数目为0.所以有

若考虑从Ti中任意顶点到Tj中任意顶点对W(Un)的贡献,在W1(Un)中已经分别考虑了Ti,Tj中的边的贡献,故接下来只需要再考虑圈上的边对W(Un)的贡献.那么从顶点vi到顶点vj的路径上的任一边e∈E(Cm),其对W(Un)的贡献为经过该边e的次数,而Ti中的顶点到Tj中顶点经过这条边e次数共有|Ti|·|Tj|次.接着考虑顶点vi到顶点vj的边数,其中j>i,若,那么顶点vi到顶点vj的边数为j−i;若,那么顶点vi到顶点vj的边数为m−(j−i),即其边数为

故从Ti中顶点到Tj中顶点中圈上的边对W(Un)的贡献为|Ti|·|Tj|·gij.而对于任意的两个Ti,Tj,(i

故W(Un)=W1(Un)+W2(Un),证毕.

接着用定理1中的公式来求W(G).W1(G)=1·1·8·3+2·7+3·6·2=74,W2(G)=1·4·1+1·4·1+4·4·1=24.故W(G)=74+24=98.通过两种方式对比会发现,用定理1来求图的Wiener指标时会更加简洁,不需要求一些中间量的值,而是直接简单利用顶点的数目就能求得结果.

图2 单圈图G

事实上,公式(1)与公式(6)是可以相互转化.注意到公式(1)中,对于Un−E(Cm)剩下来的所有分支树没有区分平凡与非平凡,所以在式(2)与式(4)可以放在一块讨论.此时的wi=dTi(vi),i=0,1,···,m−1.当分支树Ti平凡时,则W(Ti)=0,wi=0.

致谢:本文得到数字福建气象大数据研究所和数据科学与统计重点实验室的资助.