云制造中带学习效应平行机排序问题的最优可中断算法
蒋义伟, 张振宇, 魏 麒, 季 敏
(1.浙江工商大学管理工程与电子商务学院,浙江杭州310018;2.宁波财经学院国际经济贸易学院,浙江宁波315100)
§1 引 言
云制造是云计算,大数据,物联网等技术上发展起来的一种新型制造模式,以互联网为纽带将分散在各地的制造资源整合在一起,然后通过云平台发布制造资源当前的使用状况,通过资源整合和共享完成生产制造,极大地提高资源的利用率和生产效率.本文主要研究云制造环境下的带有学习效应的平行机排序问题,目标是在一定费用约束下,如何购买资源并给出最优的生产调度方案.
本文分别针对两类学习效应函数给出了最优的可中断算法,目标是在所有加工费用不超过给定的总费用ˆU的情况下,极小化最大完工时间,即Makespan.机器Mi的单位时间加工费用为li,考虑以下加工费用依赖于时间变化的两种学习效应函数.第一种学习效应函数是基于指数函数的DeJong学习效应函数,即
L1=li(M+(1−M)e−αt)(0≤M<1,α>0).
第二种是基于幂函数的学习效应函数,即
L2=li(M+(1−M)(t+1)α)(0≤M<1,α<0).
从上述函数中可以看到,随着t不断增大,机器Mi的加工成本不断减少并趋于一个常量Mli,这里M(0≤M<1)是一个不可压缩因子,即加工费用最多可以降到原来的(M∗100)%.本文主要考虑工件可中断情况,可中断是指工件可以在加工过程中被中断,剩余部分可在后续的时间在任意机器上加工.对于上述两个模型,按照排序问题的三参数法可表示为Pm|pmtn,Li,U≤|Cmax,i=1,2.
2009年李伯虎等[1-3]首先提出了云制造这一概念并对其进行了定义.现有的大多数文献主要研究云制造的服务模式以及服务技术层面[4-6],很少考虑云制造环境下的资源调度和生产管理问题.Li等[7]首先研究了云制造环境下的平行机排序问题Pm|U≤|Cmax,分别考虑工件可中断与不可中断情形.对于可中断情形,给出了一个最优解算法,对于不可中断情形,设计了一个最坏情况界为2的近似算法.此后,Li等[8]研究了机器带有固定租用成本的同类机排序问题Qm|U≤|Cmax,针对机器速度越大,机器速度与机器费用比值也越大的特殊情况,分别给出了可中断和不可中断近似算法.刘淑丹等[9]则给出了同类机情形下更一般的结果.
与上述问题密切相关的研究为带机器购买费用的平行机在线排序问题.Noga等[10]首次研究了带机器费用的在线排序问题,对于机器购买费用为单位费用情形,分别给出了工件两种到达方式下的在线算法和下界,Dósa等[11]改进了上述结果.Imreh[12]和Jiang等[13]分别研究了两种不同加工成本的机器和可中断情况下的在线排序问题.Rustogi等[14]研究了增加机器数目对极小化最大完工时间和总完工时间的影响.此外Jiang等[15]和Lee等[16]分别研究了半在线情况和双目标函数问题,给出了相应的近似算法.
学习效应问题的研究,Wright等[17]首次在制造业中提出了学习效应后,Gawiejnowic[18]将学习效应引入到排序领域,Biskup等[19]在排序中引入了学习效应函数Pjr=jra,其中Pjr是工件Jj在位置r上的实际加工时间,j是工件Jj的正常加工时间,a是学习因子.但是这个学习效应函数有不足之处,即当加工足够多的工件时,工件所需的加工时间会趋向于零.因此,根据Wrigh提出的学习的定义,DeJong等[20]提出了基于两种假设的新模型,第一是随着时间的推移,公司的技术,设备和管理组织会逐渐完善,第二个是最终这两种改善会逐渐稳定.基于上述假设,他提出了一个新的学习效应函数Ts=T1(M+(1−M)/sm),其中Ts表示第s个产品生产的时间,T1表示第1个产品生产的时间,M表示不可压缩因子(0≤M≤1),m是个学习因子(0 §2给出问题的具体描述和符号定义.§3给出问题Pm|pmtn,Li,U≤|Cmax最优排序的一些相关性质.§4给出问题Pm|pmtn,Li,U≤|Cmax的最优算法.§5总结全文并讨论今后的研究方向. 本节主要给出问题的具体描述以及所需要的符号定义. 问题具体描述如下:给定工件集J={J1,J2,···,Jn},工件Jj的加工时间为pj,工件的总长度为.机器集合表示为M={M1,M2,···,Mm},机器Mi的单位时间加工费用为li,不失一般性,假设l1≤l2≤···,lm.假设σ是n个工件的可行排序,Cj(σ)为Jj的完工时间,则可行排序σ的目标函数Makespan 可表示为.记为机器Mi的完工时间,由于机器的加工费用依赖于时间变化,根据两种学习效应模型L1和L2,机器Mi上产生的总加工费用分别为 为了方便叙述,引入以下符号.记pmax为所有工件中最大的工件长度,为所有工件在j台机器上加工的最优目标函数值.分别记Cmax(A)和Cmax(opt)为算法A的目标函数值和最优排序的目标函数值. 本文主要研究了云制造环境下带学习效应的平行机排序问题,目标是在不超过预算成本的情形下极小化最大完工时间,对两种学习效应函数给出了统一的最优可中断算法.后续的研究将考虑工件不可中断情形,由于该问题是NP-难问题,将主要考虑其近似算法的设计与分析或者多项式时间近似方案(PTAS).此外可将此类问题的机器环境推广到同类机情形.§2 问题描述和符号定义
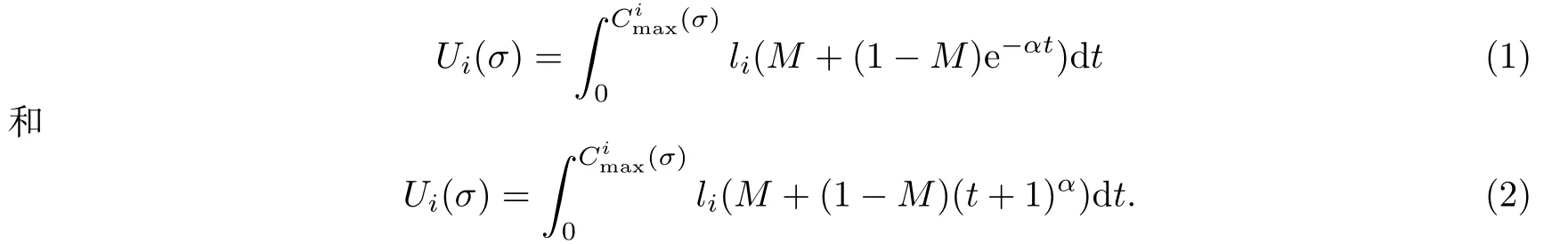
§3 初步结论



§4 最优算法



§5 总结和进一步讨论

