Sobolev方程的H1-Galerkin时空混合有限元分裂格式
常晓慧,李 宏,何斯日古楞
(内蒙古大学数学科学学院,内蒙古呼和浩特010021)
§1 引 言
考虑具有Dirichlet边界条件的一维Sobolev方程
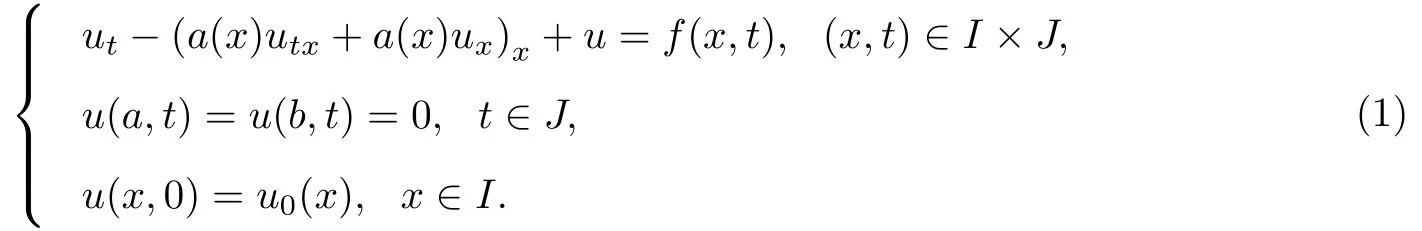
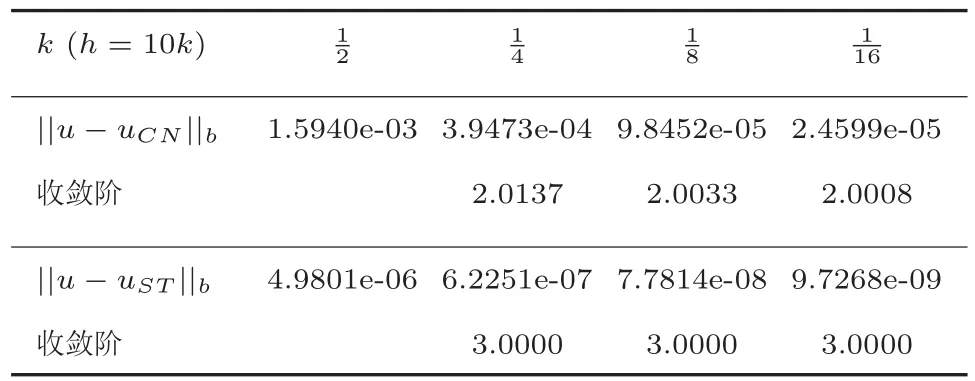
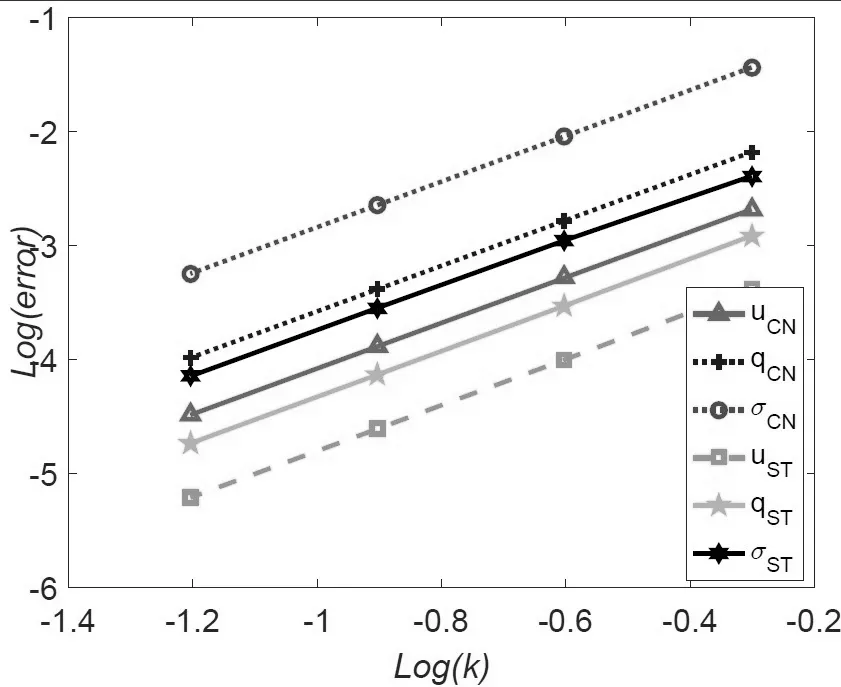
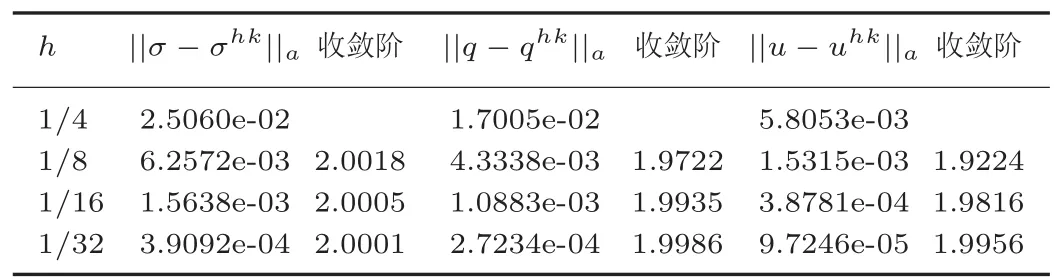
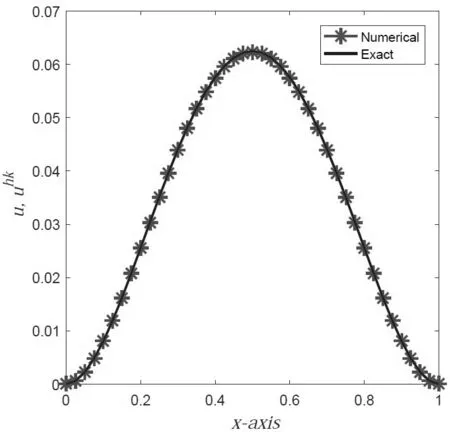
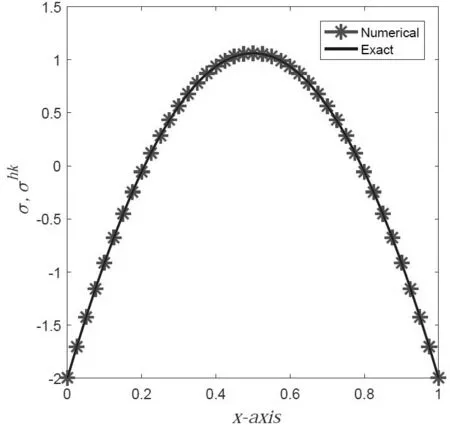
其中空间区间I=[a,b],时间区间J=(0,T].f(x,t)是源函数,u0(x)是已知初值函数,a(x)是充分光滑的有界函数,且存在正常数amin和amax满足0 Sobolev方程广泛应用于渗透理论,土壤中湿气迁移等实际物理问题,是一类重要的发展型偏微分方程.该方程刻画的流体在高聚物中的渗透和扩散现象伴随有以定常速度运动的陡峭峰线前沿,称之为non-Fickian现象.因此人们不仅关心流体在渗透和扩散中的浓度,同时还关注non-Fickian现象发生的时间与位置(浓度的梯度)和通过多孔介质时渗透流体通量(伴随向量).由于Sobolev方程实际计算域的不规则或问题本身的复杂性,解析求解比较困难,因此提出很多数值方法,如早期的差分方法[1],文[2,3]中分别利用两种不同的降阶外推有限差分方法研究Sobolev方程.用有限元方法求解也得到快速发展,文[4]中用标准Galerkin方法讨论了一维非线性Sobolev方程,证明了2≤p≤∞时的Lp误差估计;文 [5]研究了具有非线性边界条件的非线性Sobolev方程的有限元方法;文[6,7]提出了非协调有限元方法.文[8]研究了降阶外推配谱法,文 [9]讨论了降阶外推CN有限体积元法.1998年Pani在 [10]中提出H1-Galerkin混合有限元方法,并进一步应用于研究抛物型积分微分方程[11]和二阶双曲方程[12],该方法利用具有不同次数的多项式空间作为逼近空间,可以避免传统混合有限元方法中的LBB相容性条件.文[13]利用H1-Galerkin混合有限元法研究了Sobolev方程.2014年,文[14]提出了H1-Galerkin混合有限元方分裂格式,该格式能同时高精度逼近渗透流体的浓度u,梯度q和流体通量σ,不但适合处理复杂边界和小扩散系数的问题,而且满足LBB相容性条件.时空有限元方法时间和空间离散都利用有限元技术,可以在时间和空间上都得到高精度,并具有超收敛性质.该类方法被用于求解各种时间依赖问题,如波动方程[15],反应扩散方程[16],Sobolev方程[17]等. 本文构造方程(1)的H1-Galerkin时空有限元分裂格式,和已有的Sobolev方程数值格式的不同在于:基于H1-Galerkin混合有限元方法,结合分裂格式,在时空有限元框架内进行研究.该格式具有如下优点:1.具有形式时间和空间高阶精度,能同时高精度逼近渗透流体的浓度u,浓度梯度q和流体通量σ;2.避免了LBB相容性条件;3.近似空间可以利用不同次数的多项式空间;4.解耦原方程组.H1-Galerkin混合时空有限元分裂格式首次应用于Sobolev方程,证明数值解的存在唯一性,稳定性,通过引入时空投影算子,证明了三个变量的误差估计.无论是从格式构造还是理论分析方面,迄今为止都没有见到其他相关文献的报道. 本文的安排如下:§2给出了H1-Galerkin时空混合有限元分裂格式,§3证明了H1-Galerkin混合时空有限元解的存在唯一性和稳定性.§4针对不同的变量,引入不同的时空投影算子,讨论算子的性质,分三部分讨论三个变量的误差估计.§5提供数值算例验证格式的有效性和可行性以及理论分析结果的合理性.§6是结论. 引进相关的时,空投影及其性质,分三部分讨论uhk,qhk,σhk的误差估计.给出σ−σhk的时间节点tn处的L2模,区间H1(L2)模和L2(L2)模,以及整体L2(L2)模误差估计,证明q−qhk和u−uhk的L2(L2)模误差估计. 本文所构造格式统一时间和空间变量,因此一维问题(1)可视为关于时间变量t和空间变量x的二维问题.将二维区域[0,1]×[0,1]剖分成m×n个矩形单元.时间和空间方向分别采用线性和二次多项式作为基函数,数值求解问题(1),并与文献[14]的分裂型H1-Galerkin混合格式做了比较. 表1 用线性基函数和时,关于空间方向的误差和收敛阶 表1 用线性基函数和时,关于空间方向的误差和收敛阶 h ||σ−σhk||a收敛阶 ||q−qhk||a 收敛阶 ||u−uhk||a收敛阶1/4 2.5060e-02 1.7005e-02 5.8053e-03 1/8 6.2572e-032.0018 4.3338e-03 1.9722 1.5315e-03 1.9224 1/16 1.5638e-032.0005 1.0883e-03 1.9935 3.8781e-04 1.9816 1/32 3.9092e-042.0001 2.7234e-04 1.9986 9.7246e-05 1.9956 表2 用线性基函数和时,关于时间方向的误差和收敛阶 表2 用线性基函数和时,关于时间方向的误差和收敛阶 k ||σ−σhk||a收敛阶 ||q−qhk||a 收敛阶 ||u−uhk||a收敛阶1/2 2.6441e-02 3.9803e-03 1.1487e-03 1/4 6.6022e-032.0017 9.9330e-04 2.0026 2.8656e-04 2.0031 1/8 1.6501e-032.0004 2.4776e-04 2.0033 7.1391e-05 2.0050 1/16 4.1260e-041.9997 6.1719e-05 2.0052 1.7742e-05 2.0086 表1和表2中出现的||·||a为||·||L2(0,T;L2(I)).表1和表2分别采取线性基函数和一个剖分步长固定,而另一步长折半减少的方式分析||σ−σhk||L2(0,T;L2(I)),||q−qhk||L2(0,T;L2(I))和||u−uhk||L2(0,T;L2(I))的误差和收敛阶.从表中数据可以看出,当一个步长折半递减时,三项误差的收敛阶均接近二阶最优收敛.图1,图2和图3分别给出时空线性基函数并取步长时真解u,q,σ和数值解uhk,qhk,σhk的对比图.实验数据说明本文所提出时空格式能够有效求解Sobolev方程,且理论分析结果合理. 表3和表4中出现的||·||b表示为t=T时刻的||·||L2(I).表3,表4,图4和图5中,uCN和uST分别表示文献[14]的分裂型H1-Galerkin混合格式和本文所提时空格式所得数值解.从表3和图4的数据可知,本文采用的时空线性多项式基函数的方法和文献[14]中利用的空间线性多项式基函数方法相比,未知量u,q,σ的收敛阶均为二阶,但是本文所提时空格式的误差明显小于文献[14]方法的误差. 从表4和图5的数据可以看出,文献[14]中利用空间二次多项式基函数的格式收敛阶为二阶,而本文中利用时空二次多项式基函数的方法对u,q,σ的收敛阶达到三阶,本文所提时空格式通过增加时间基函数多项式次数可提高收敛阶数和计算精度且允许用大时间步长. 图1 线性基函数,u和uhk的对比 图2 线性基函数,q和qhk的对比 图3 线性基函数,σ和σhk的对比 该研究通过引进两个辅助函数,构造了一维Sobolev方程的H1-Galerkin时空混合分裂格式,该格式不但具有时空高阶精度,且能同时高精度逼近渗透流体的浓度u,浓度梯度q和流体通量σ,还解耦方程组.讨论了H1-Galerkin时空混合有限元解的稳定性,存在唯一性和误差估计.Sobolev方程的H1-Galerkin时空混合有限元分裂格式是首次给出,研究内容和结论是Sobolev方程混合时空类方法理论研究的新进展.通过引入时空投影算子,证明误差分析的理论迄今为止还没有见到相关文献研究.本文给出了一维Sobolev方程的格式建立和理论分析的详细过程,并通过数值结果可以看出H1-Galerkin时空混合分裂格式的有效性和可行性以及理论分析结果的合理性.鉴于此,该格式构造和误差分析的思想和方法可以很自然地推广到多维情形. 表3 线性基函数,t=T时刻的误差和收敛阶 表4 二次基函数,t=T时刻的误差和收敛阶 图4 线性基函数,t=T的收敛阶对比 图5 二次基函数,t=T的收敛阶对比§2 H1-Galerkin混合时空有限元分裂格式



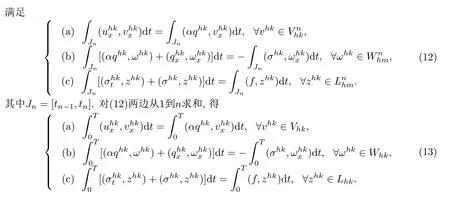
§3 数值解的稳定性和存在唯一性


§4 数值解的误差估计
4.1 σhk的误差估计




4.2 qhk的误差估计


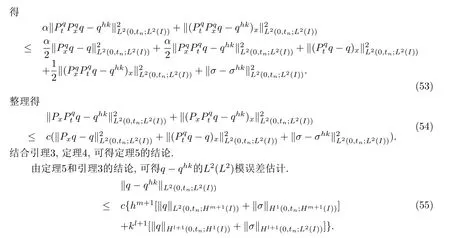
4.3 uhk的误差估计

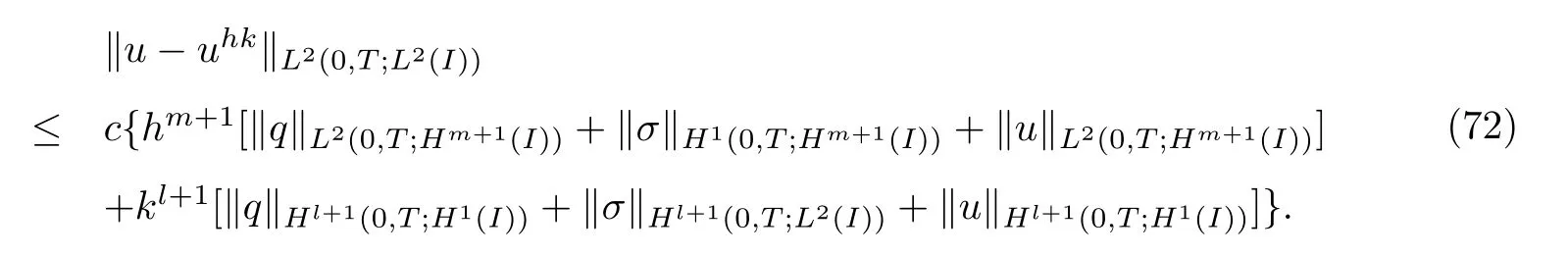
§5 数值算例



§6 结束语