一类二阶变系数线性微分方程的求解探讨
陶筱平
(黄冈师范学院 数学与统计学院,湖北 黄冈 438000)

1 相关研究
记系数为一次函数的二阶变系数线性微分方程为
(d1x+d0)y″+(p1x+p0)y′+(q1x+q0)y=0
(1)
由于二阶常系数齐次线性微分方程y″+py′+qy=0,是在借助于函数y=erx解决了求通解的问题[9], 而在研究变系数微分方程的解时,也常常借助到形如y=erx的函数[10]. 对于方程(1),本文将通过相关定理和推论,推导其具有y=xkerx形式解的条件,进而寻求它的y=xkerx型特解的具体方法和公式.
1.1 方程存在特解的条件
定理方程(1)存在y=xkerx型的特解的充要条件是方程(1)系数中的d1,d0,p1,p0,q1,q0满足线性方程组

(2)
证明充分性:若y=xkerx是方程(1)的解,将y=xkerx、y′=(rx2+kx)xk-2erx、y″=(r2x2+2krx+k2-k)xk-2erx代入方程(1),可得(r2d1+rp1+q1)x3+(2krd1+r2d0+kp1+rp0+q0)x2+[(k2-k)d1+2krd0]x+(k2-k)d0=0,由此可知方程组(2)成立.
必要性:若方程(1)系数中的d1,d0,p1,p0,q1,q0满足线性方程组(2),则有(r2d1+rp1+q1)x3+(2krd1+r2d0+kp1+rp0+q0)x2+[(k2-k)d1+2krd0]x+(k2-k)d0=0,整理得
(d1x+d0)(r2x2+2krx+k2-k)+(p1x+p0)(rx2+kx)+(q1x+q0)x2=0,
从而可得
(d1x+d0)(r2x2+2krx+k2-k)xk-2ex+(p1x+p0)(rx2+kx)xk-2ex+(q1x+q0)xkex=0.
设y=xkex,即得
(d1x+d0)y″+(p1x+p0)y′+(q1x+q0)y=0,
所以y=xkex是方程(1)的解.证毕.
当定理中k=0时,则线性方程组(2)变为线性方程组(3)
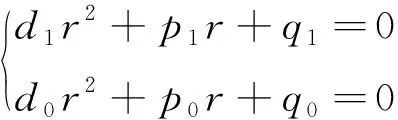
(3)
所以有
推论1方程(1)存在y=erx型的特解的充要条件是r是特征方程d1r2+p1r+q1=0和d0r2+p0r+q0=0的相同特征根.
推论2r≠0时,线性方程组(3)的任一组解
代入方程(1)所得方程必有特解y=erx.
当定理中k=1时,有如下推论

另外,当y=xerx是方程(1)的特解时,必有
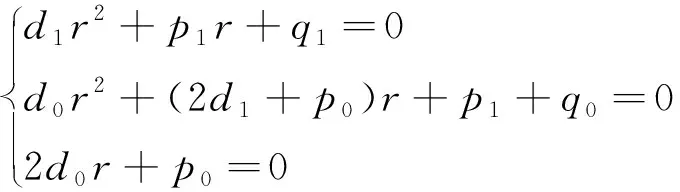
(4)
因此,有下述推论
推论4r≠0时,线性方程组(4)的任一组解
代入方程(1)所得方程必有特解y=xerx.
1.2 方程存在特解的判断方法
讨论方程(1)具有y=xkerx类型特解的判断方法.
类型一:方程(1)中d0=0的情形

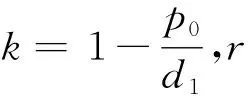
类型二:方程(1)中d0≠0的情形
此时,必有k=0或k=1.
若取k=0,由上述定理知,当特征方程d1r2+p1r+q1=0,d0r2+p0r+q0=0有相同特征根r,方程(1)才有特解y=erx.
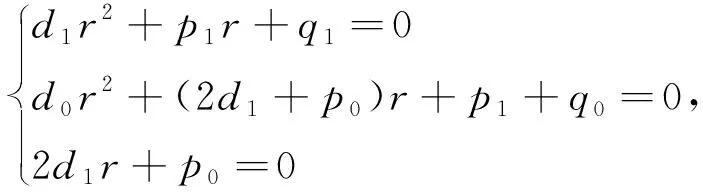
综上,得下述结论
结论1不是任意方程(1)都有y=xkerx型的解,只是部分满足一定条件的方程(1)才有y=xkerx型的解.
此时,有的方程只有一个y=xkerx型的解,有的方程有两个y=xkerx型的相异解(此时可以写出方程的通解).
结论2当方程(1)中d0≠0时,方程至多只有y=erx或y=xerx这两种形式的解.
结论3可以利用定理中的条件,反向构造具有y=xkerx型特解的方程.
如以特解y=xerx为例,由推论4知,将线性方程组(4)的某一组解d1,d0,p1,p0,q1,q0代入方程(1)中,即可得到一个以一次函数为系数的非常系数线性微分方程,该方程有特解y=xerx.
2 应用
应用1求解方程(1)的特解问题
例1求微分方程(x-1)y″-xy′+y=0的y=xkerx型的特解.
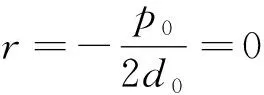
例2求微分方程xy″-2(x+1)y′+(x+2)y=0的y=xkerx型的特解.
分析由于d0=0,所以归属为类型一,可求得方程的两个特解y=ex和y=x3ex,所以该方程通解为y=(c1+c2x3)ex.
应用2构造具有特型特解的方程(1)问题
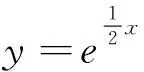
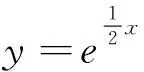
(10x-1)y″-(x-1)y′-2xy=0,
2(x+1)y″-(x-1)y′-y=0,
2(x-4)y″+(x-2)y′-(x-3)y=0.
例4构造具有特解y=xe-2x的微分方程(d1x+d0)y″+(p1x+p0)y′+(q1x+q0)y=0.
分析在线性方程组(4)中任取一组解代入方程(1),得到的方程有特解y=xerx.要构造具有特解y=xe-2x的方程,由推论4知此时线性方程组(4)为

(5)
其通解为
在其中每取一组解代入方程(1),得到的方程均有特解y=xe-2x.故所求方程有许多,如
(4x+1)y″+4(3x+1)y′+8(x+1)y=0
(6x+1)y″+4(3x+1)y′+4xy=0
例5构造具有特解y=x3e2x的微分方程(d1x+d0)y″+(p1x+p0)y′+(q1x+q0)y=0.
分析由结论2知,此时方程(1)中的系数d0=0,线性方程组(2)为

(6)
其通解为
在其中每取一组解代入方程(1),得到的方程均有特解y=x3e2x,故所求方程有许多,如
xy″-(3x+4)y′+(2x+1)y=0
xy″-2(2x+1)y′+4(x+1)y=0
以上构造的方程均可通过类型一和类型二进行验证.
通过上述的讨论,本文得出了判断系数为一次函数的二阶变系数线性微分方程(1)有y=xkerx型特解的充要条件,将方程特解的存在问题转化为方程(1)系数中的常数d1,d0,p1,p0,q1,q0是否满足线性方程组(2)的问题,并找到了求方程的y=xkerx型特解的具体求解方法. 本文是对二阶变系数齐次线性微分方程求解问题研究的有益补充.

