多尺度法与平均法对新月形覆冰导线舞动特性的影响

闵光云， 刘小会， 严 波， 孙测世， 蔡萌琦

(1.重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室， 重庆 400074； 2.重庆交通大学土木工程学院， 重庆 400074； 3.重庆大学航天航空学院， 重庆 400044； 4.成都大学建筑与土木工程学院， 成都 610106)

随着中国电网技术的高速发展，覆冰导线的舞动已经引起很多学者的关注，但由于覆冰的多样性与不确定性，防止导线舞动这一课题的进步一直很缓慢[1]。大幅度的舞动将会造成线路频繁跳闸与停电，而长时间大幅振动所产生的交变张力会使得螺栓松动或损坏[2]。关于舞动发生的原因，Den-Hartog[3]提出了竖向失稳机理，而以Nigol[4-5]为代表的学者提出的二自由度耦合的舞动机理。

气动力系数是研究覆冰导线舞动的重要参数，为研究覆冰导线舞动，许多学者在这一领域做了很有意义的研究。李万平等[6]通过对特大厚度覆冰导线进行风洞测试得知，双分裂导线试验有尾流影响时的气动力幅度显著低于单导线的情形。王昕等[7]针对新月形和D形两种典型断面的特高压大截面厚覆冰导线进行了气动力系数风洞测试,获得了很有意义的结论，给实际工程提供了指导意见。楼文娟等[8]对4种不同厚度的新月形截面导线进行了气动力特性风洞试验，获得了0°～180°攻角间单导线、二分裂导线及四分裂导线的气动三分力系数。严波等[9]测试了不同冰厚和不同风速下的覆冰四分裂导线静态空气动力系数，其结果表明尾流效益对气动力系数有明显的影响。

风洞试验所得的气动力参数是研究覆冰导线的舞动的重要参数，且导线的舞动属于非线性振动[10-14]，就非线性振动问题学者们提出了许多经典的定量分析方法，比如多尺度法、谐波平衡法、平均法等。不同的解析方法具有不同的优点、缺点，采用何种方法研究导线的舞动最为适合还少有人研究，基于此，首先通过风洞试验获得覆冰单导线的气动力系数，接着采用平均法与多尺度法研究了覆冰导线的舞动特性，最后通过对比该两种方法下覆冰导线舞动特性差异，以了解哪一种方法最为适合。

1 风洞试验

为了获取新月形覆冰导线的空气动力系数，在中国空气动力研究与发展中心进行测试，本次试验依据《大型试验质量管理要求》(GJB 1452—1992)在低速所1.4 m×1.4 m风洞进行。

本次试验需用到的天平的实体图像如图1所示。使用该天平来测试覆冰导线模型的阻力、升力以及扭矩。

图1 天平

图2 风洞测试空气动力系数

采用拟静态方法，选取一段输电线模型，进行气动参数测试。1.4 m×1.4 m低速风洞如图2(a)所示，测试模型如图2(b)所示，覆冰冰型为新月形，模型如图2(c)所示。当风流经过该覆冰导线时，可根据测力天平可以测量新月形覆冰导线受到的升力、阻力和扭矩。

覆冰单导线静态空气动力特性试验测得的空气动力系数包括阻力系数、升力系数和扭矩系数，且无量纲空气动力参数定义为

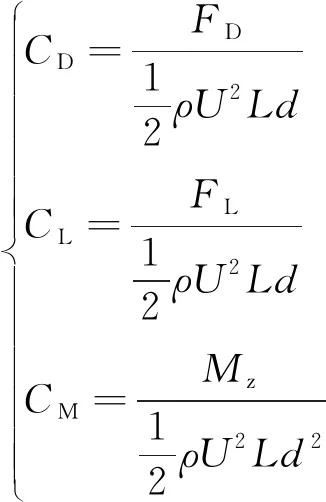
(1)

式(1)中：FD、FL、MZ分别为导线所受的阻力、升力、扭矩；ρ为空气密度；U为平均风速；L为导线有效长度；d导线直径。通过风洞试验测得12 mm冰厚的新月形覆冰单导线在10 m/s风速作用下空气动力系数随风攻角的变化曲线如图3所示。

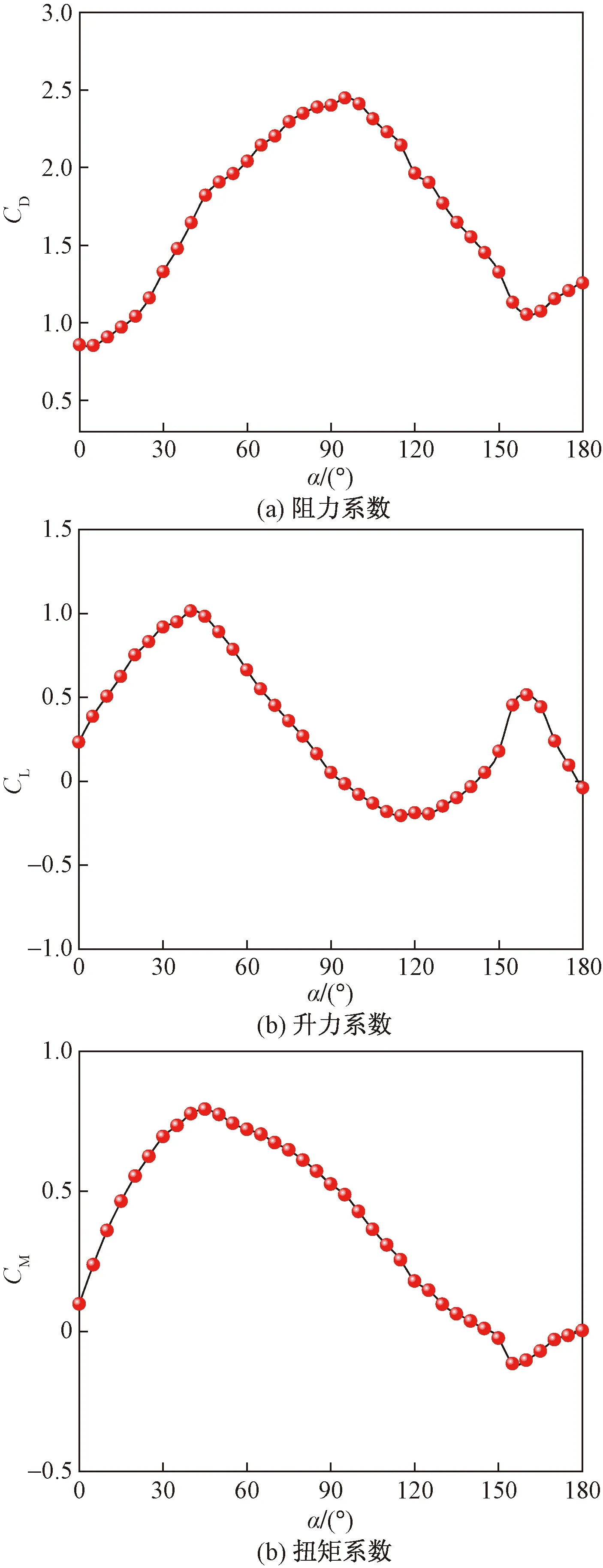
图3 覆冰单导线空气动力系数

由图3可知：CD随着攻角α整体变化的规律具有两端低、中间凸的特点；覆冰单导线气动升力系数曲线CL随着攻角α整体变化规律随着攻角的增加由正到负变化；CM的变化规律与CL的变化规律大致相同，但当攻角等于150°左右时CL呈下降趋势CM迎来新的上升期。根据Den Hartog驰振原理[10]，当覆冰导线受到水平方向风作用时，水平方向会开始振动，由于水平方向的振动，当竖直方向由于覆冰变为非圆形截面的导线受到负斜率的气动升力CL的作用时导线很容易发生舞动，2节将针对具体的输电线路，应用定量分析法研究覆冰导线的舞动。

2 单档输电导线自由振动数学模型

建立如图4所示导线振动力学模型，导线两端用固定铰链约束。为了给出导线的动力学方程，建立笛卡尔坐标系，选取左端悬挂点为坐标原点，x轴沿着两悬挂点的连线方向，y轴竖直向下，然后根据x轴与y轴确定垂直平面向里的z轴方向。

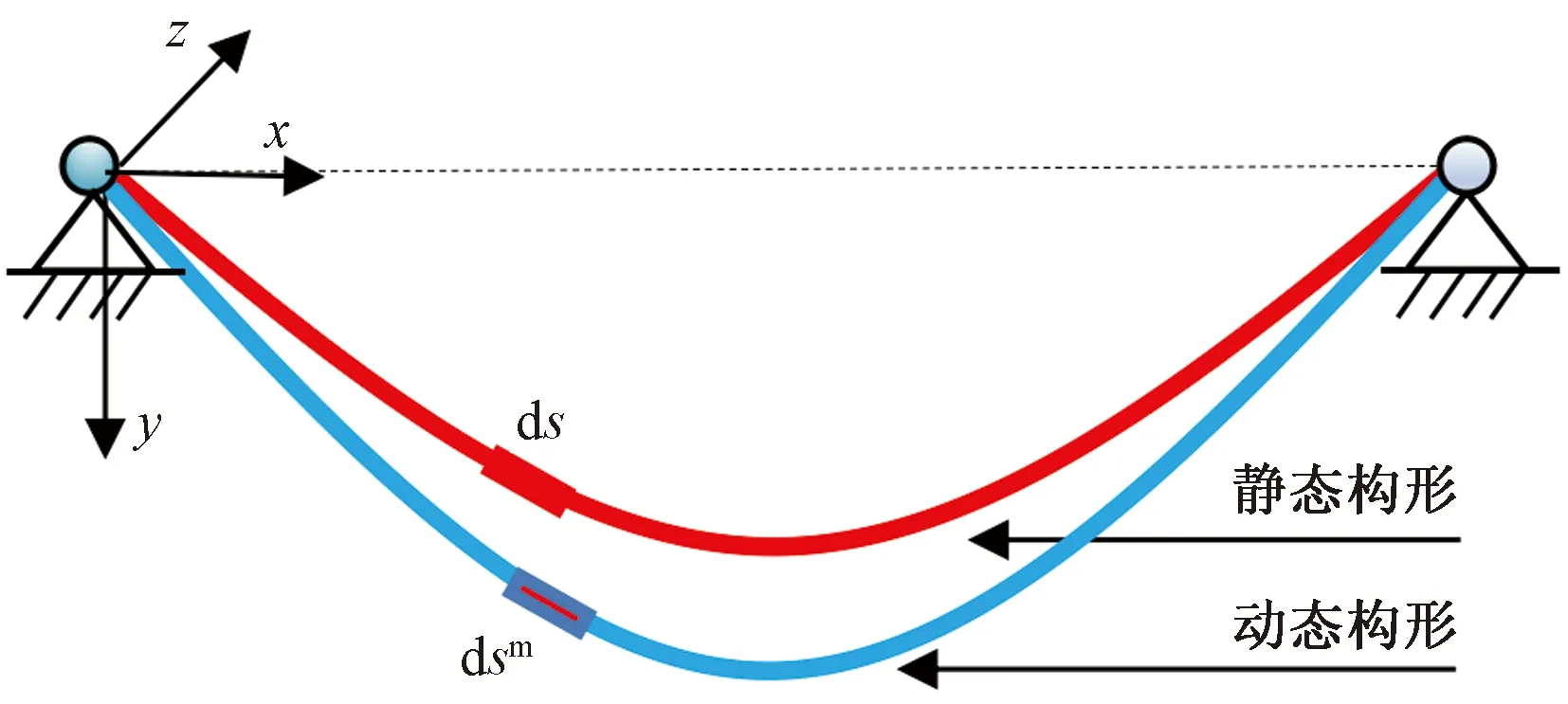
图4 单档导线力学模型

在重力作用下导线静态构形上选取长度为ds的微元，接着在其他外部载荷作用下导线动态构型上选取长度为dsm的微元，该位置处导线轴向应变为

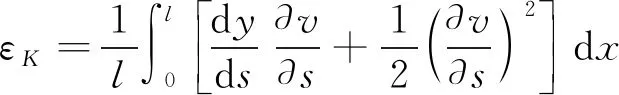
(2)

式(2)中：y为覆冰导线的静态构型曲线；v为覆冰导线竖向的动态位移；s为弧坐标；x为位置坐标；l为覆冰导线的跨径。

由哈密顿变分原理可得

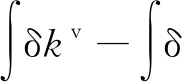
(3)

式(3)中：δkv为系统的动能；δ∏为系统的势能；δw′为系统保守力所做功。

根据式(3)可得知覆冰导线的舞动控制方程为

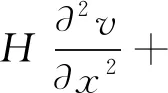
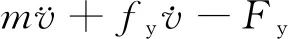
(4)

式(4)中：m为覆冰导线单位长度上的质量；fy为黏性阻力系数；Fy为气动力；EA为导线的抗拉刚度；H为导线的静态张力。

为便于下文应用多尺度法与平均法研究覆冰导线的舞动特性，现将该过程涉及的覆冰导线物理参数列出，如表1所示。因为覆冰导线的振动主要受基本模态的影响，因此应用一阶模态截断法，模态函数选取ψ(x)=sin(πx/l)，导线长度选取l=300 m。

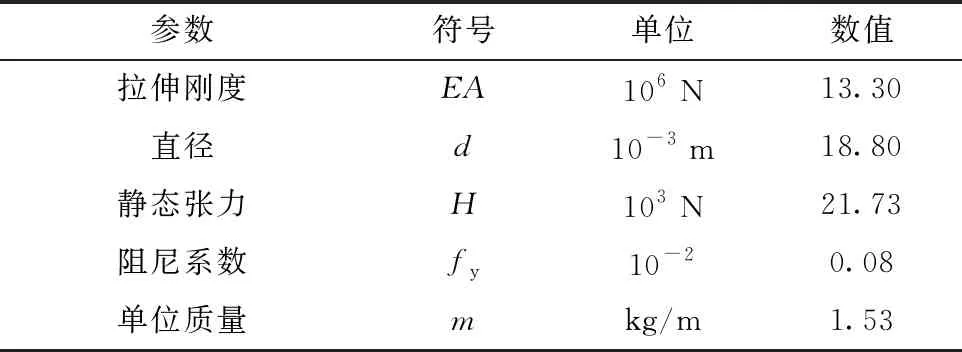
表1 导线的物理参数

2.1 多尺度法

覆冰导线的舞动特征为大位移、小变形，属于几何非线性特点。而在科研领域中学者们对于非线性系统的定量分析一般选用多尺度法。基于Galerkin方法转变覆冰导线的舞动控制方程[式(4)]为

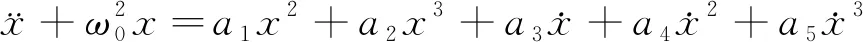
(5)

式(5)中：ω0表示固有频率；a1、a2为导线自振的非线性系数；a3为导线阻尼与负斜率气动力系数之和；a4、a5为气动力引起的非线性系数。

为方便控制方程的处理，令

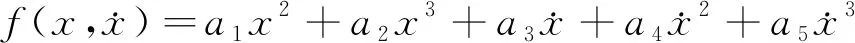
(6)

把覆冰导线当成弱非线性振动系统，则其控制微分方程可以表示为

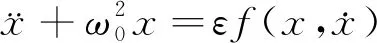
(7)

式(7)中：ε表示无量纲小参数。

可将式(7)的解设为

x=x0(T0,T1)+εx1(T0,T1)+ε2x2(T0,T1)+…

(8)

式(8)中：T0、T1表示两个时间尺度(T0=t,T1=εt)且满足：

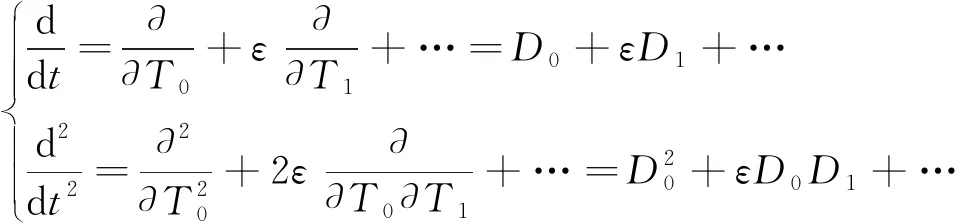
(9)

将式(8)代入式(9)可得：

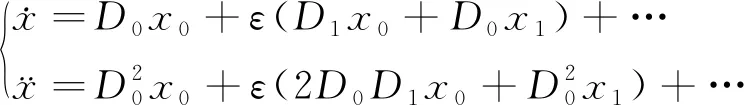
(10)

将式(10)代入式(6)，并整理包含ε0项的系数、ε1项的系数，且令该两项系数等于零可得到：

ε0阶为

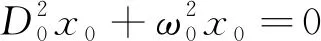
(11)

ε1阶为

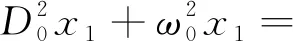
a5(D0x0)3

(12)

令

x0=A(T1)eiω0T0+cc

(13)

式(13)中：A表示覆冰导线的舞动幅值；cc表示式(13)的共轭项。

将式(13)代入式(12)可得：

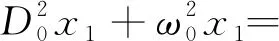
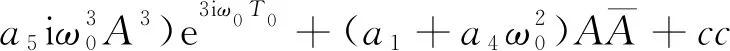
(14)

只有消除永年项式(14)才满足有解的条件，则令

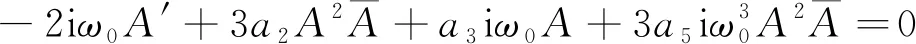
(15)

为方便计算，先引入极坐标函数：

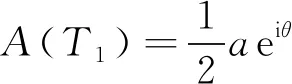
(16)

式(16)中：a表示幅值；θ表示相位。

将式(16)代入(14)并且分离虚部和实部可得到

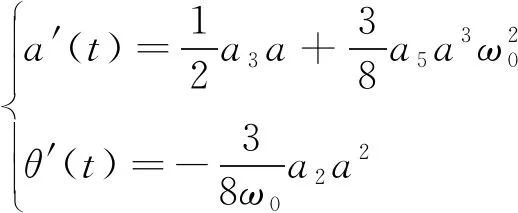
(17)

式(17)可通过Newton-Raphson method求解。

将式(17)的求解结果与式(13)一起代入式(8)可求导覆冰导线舞动的二阶近似解，再根据该近似解可画出覆冰导线振动的相平面图与位移时程图，如图5和图6所示。

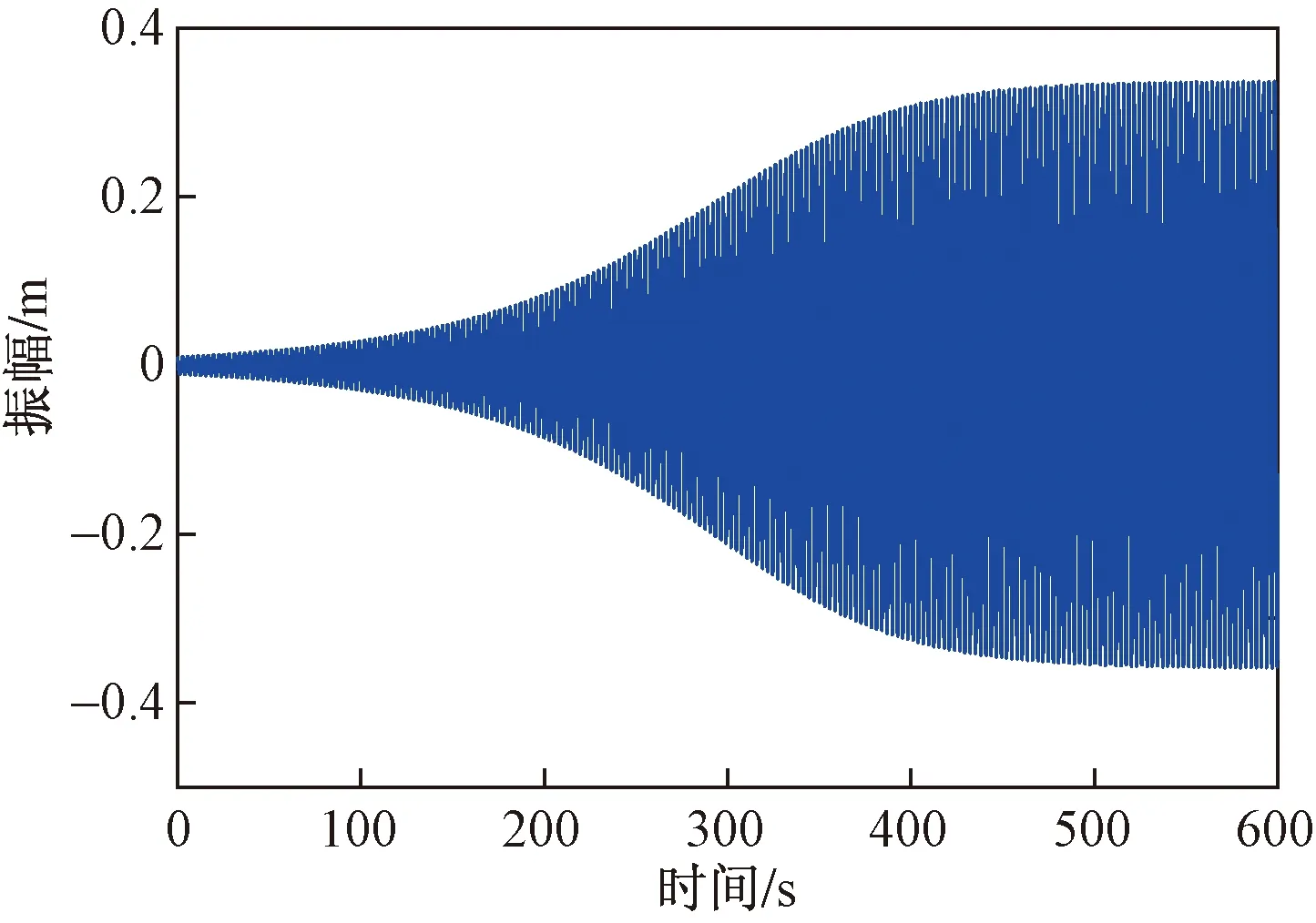
图5 位移时程曲线(多尺度法)

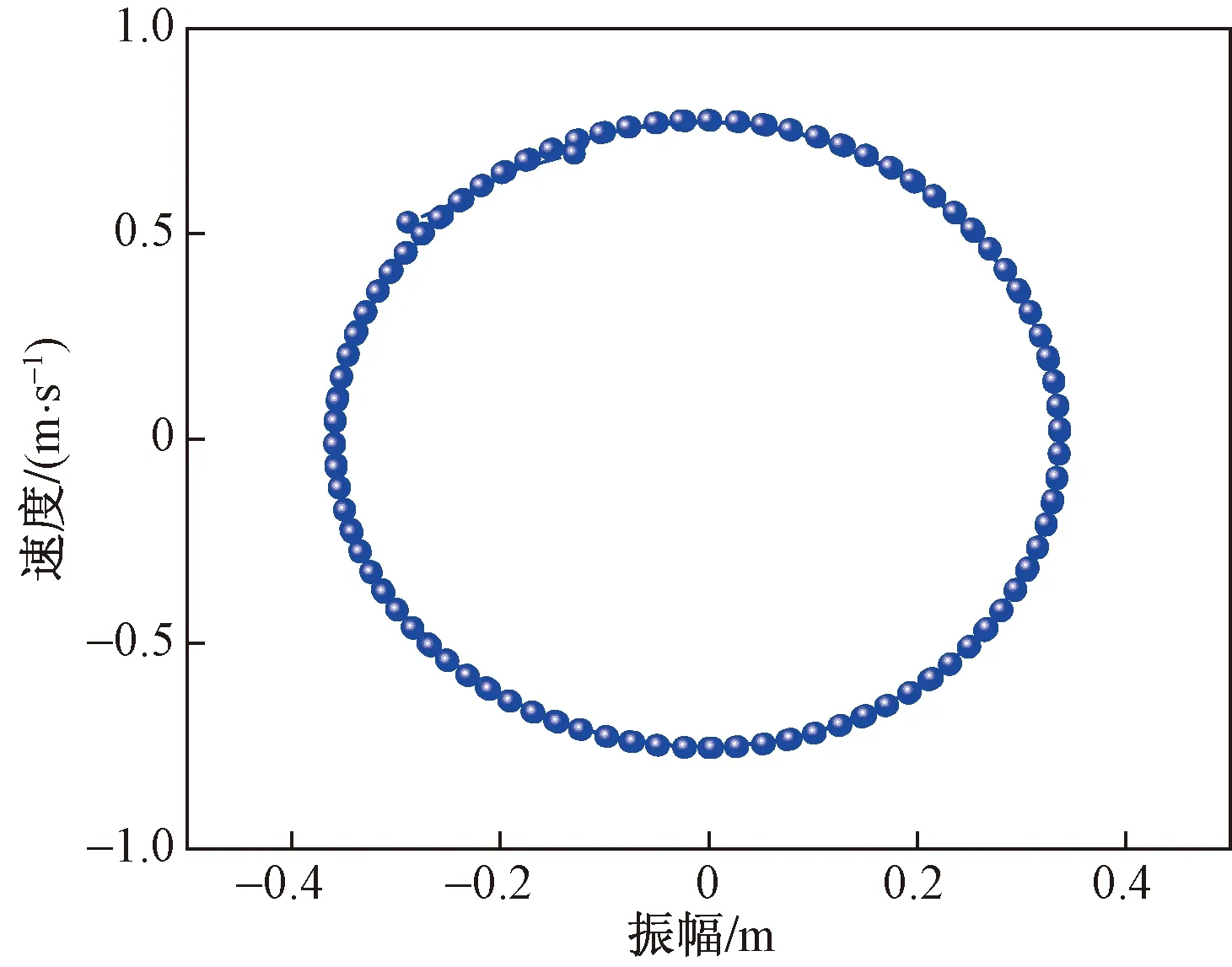
图6 相平面图(多尺度法)

通过图5、图6得知覆冰单导线稳定后的负向振幅可达0.36 m，正向最大振幅可达0.34 m，覆冰导线的极限环为以圆心为原点的极限环，且根据式(8)可得知由于小参数的存在，覆冰导线的位移曲线会出现飘逸现象，即正幅值与负幅值并不完全相等，这是一个值得注意的现象。下面将通过平均法研究覆冰导线舞动，并将舞动结果与多尺度的舞动结果进行对比。

2.2 平均法

平均法由于其解答过程简单，经常被应用与非线性振动问题中。引入状态变量x和y，将覆冰导线的振动控制方程降阶，因此该弱非线性运动方程表示为

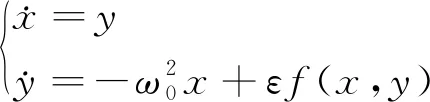
(18)

如果令引入的小参数ε=0，式(18)可转变为线性振动方程。其解为与初始条件不相关的简谐运动，且其运动方程可描述为

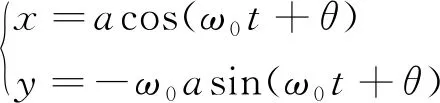
(19)

式(19)描述的是以频率为ω0做简谐运动的系统，那么其极限环可近视描述为以原点为中心的圆。如果小参数ε≠0，但无限趋近与零时，式(18)中的非线性项的影响很小，相应的解无限接近简谐运动，即所谓拟简谐运动，那么当覆冰导线受到水平方向风而发生舞动时，导线舞动的极限环必定是接近圆的封闭曲线。此时作为理论依据，可将二阶自治方程的初始响应近似表示为

x(t)=a(t)cos[ω0t+θ(t)]

(20)

式(20)中：a(t)是周期的振幅函数；θ(t)是相位函数。

将x(t)对时间求导数，得到：

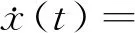
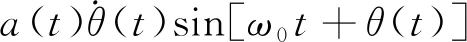
(21)

将y(t)、a(t)以及θ(t)代入式(20)并与式(21)作减法，导出约束方程为

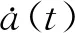
(22)

再将式(18)代入式(22)，且令

ω0t+θ(t)=φ(t)

(23)

可得到微分方程：

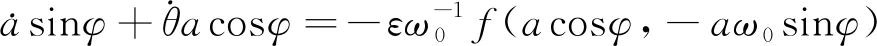
(24)

联立式(19)～式(13)方程可得：

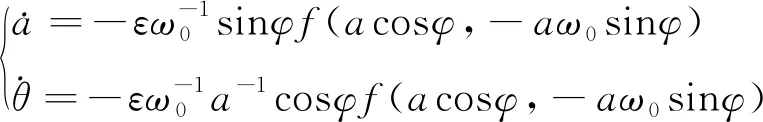
(25)

观察式(25)可得知振幅和相位的变化率都是小参数ε的同阶次小量。参数充分小时，a和θ都是时间t的慢变函数，这是平均法的理论依据，与弱非线性前提一致。

既然相位和振幅都是很小的量，故可以用一个周期内a(t)和θ(t)的平均值近视描述它们的变化过程，从而得到相应的近似算式为

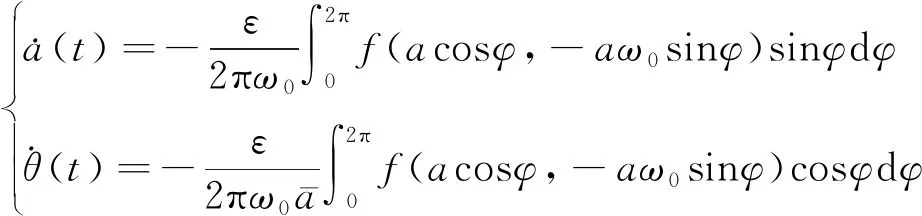
(26)

若令

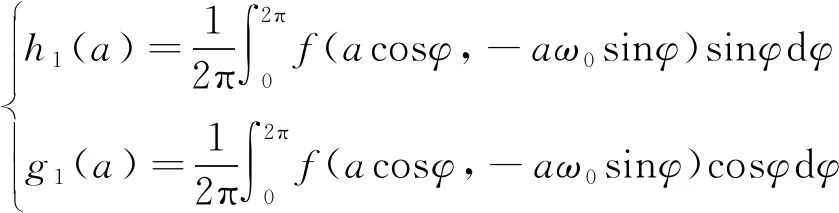
(27)

则可将计算平均振幅和平均相位的近似方程表示为

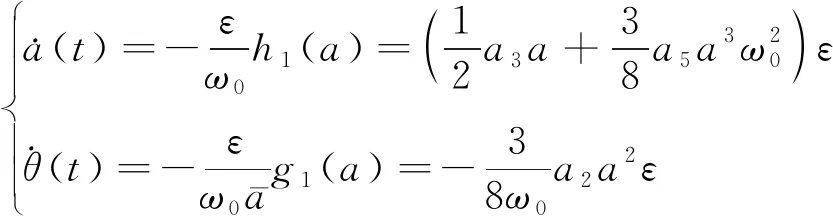
(28)

观察式(28)振幅和相位的变化率可得知与多尺度法一模一样，那么积分式(28)并且考虑初始条件为a(0)=0.01,θ(0)=0可得周期解的近似解析式为

x(t)=a(t)cos[ω0t-θ(t)]

(29)

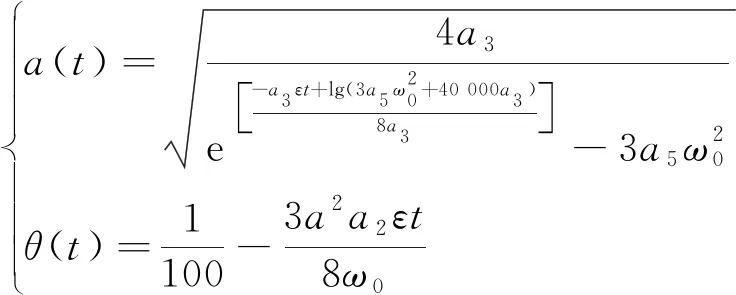
(30)

根据x的表达式可画出平均法下覆冰导线的振动位移时程曲线与相平面图，如图7和图8所示。

通过图7和图8得知覆冰单导线稳定后的负向振幅与正向振幅都为0.34 m，覆冰导线的极限环为以圆心为原点的极限环，且根据式(29)可得知平均法的计算结果没有小参数，因此导线舞动位移曲线没有发生飘逸，这与多尺度法所得结果存在差异，是一个值得注意的现象。

2.3 结果对比

为了分析平均法与多尺度法对覆冰导线舞动特性的影响，下面取两种方法下所得覆冰导线稳定后的数据做出舞动位移时程曲线与相平面图，如图9和图10所示。

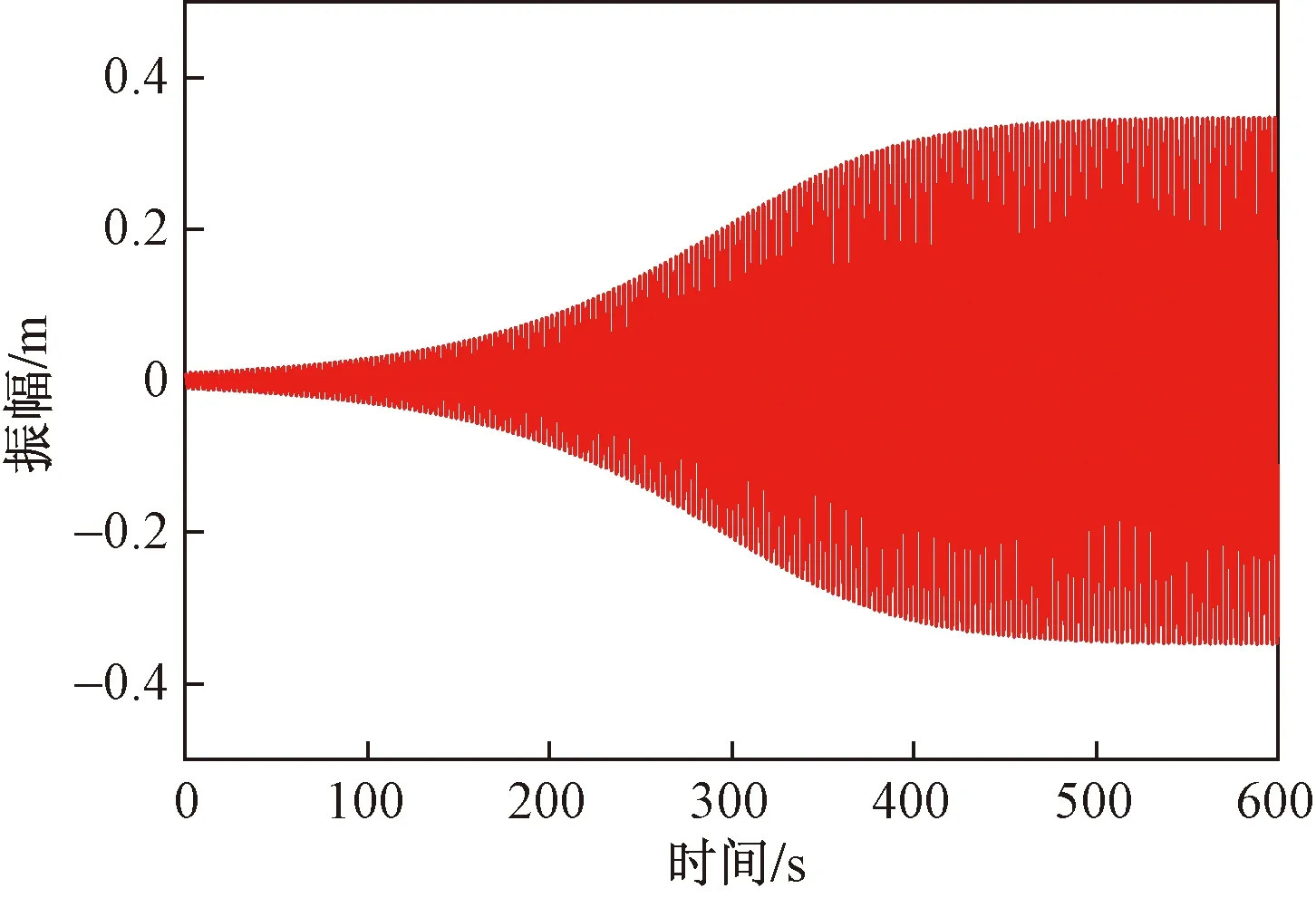
图7 位移时程曲线(平均法)

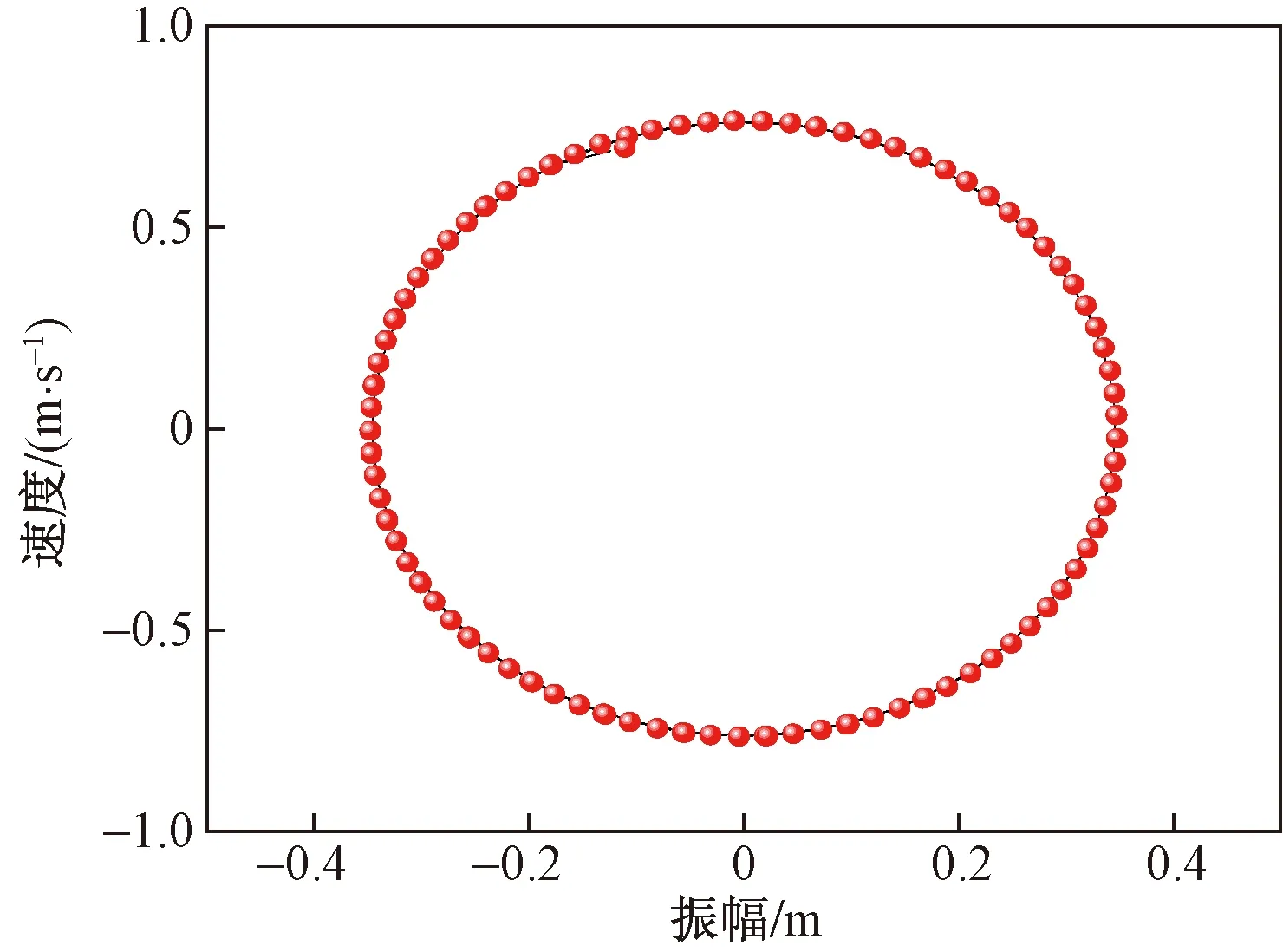
图8 相平面图(平均法)

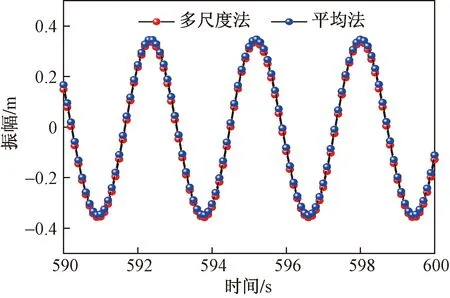
图9 位移时程曲线

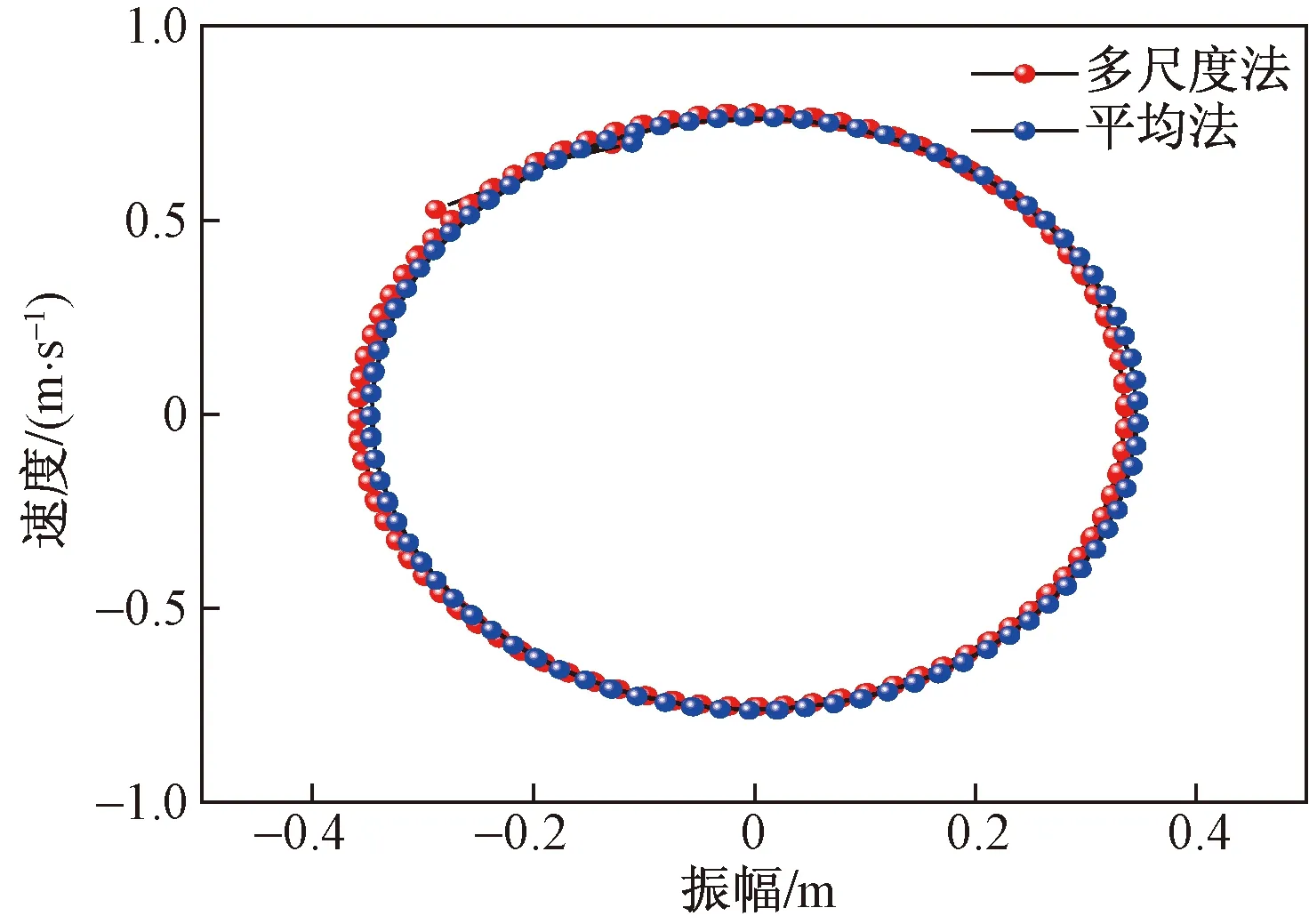
图10 相平面图

通过对比平均法与多尺度法所得的位移时程曲线可得：多尺度求解的位移时程曲线由于小参数的存在会发生飘逸，平均法求解的位移时程曲线并不会发生飘逸；尽管两种方法存在是否发生飘逸的差异，但是通过对比两者的位移曲线可得知飘逸引起的误差很小，两者的曲线几乎重合，且两者的相平面图几乎重叠，因此可认为该两种计算方法下覆冰导线的舞动特性并没有显著的差别；通过该两种计算法研究覆冰导线的舞动可得知，多尺度法的计算过程比平均法的计算过程较复杂，针对单自由度输电线路选取较为简单的平均法有助于提高工作效率。

3 结论

多尺度法与平均法所得的覆冰导线舞动位移曲线会因为小参数是否存在的原因而存在差异，多尺度法下位移曲线存在“飘逸现象”，但“飘逸现象”并不会很大程度改变舞动曲线的幅值，该两种方法的舞动位移曲线几乎重合在一起，但多尺度法的计算过程复杂，平均法的计算过程较简单，因此针对单自由度覆冰导线的舞动，平均法应首选。