2020年全国高考数学Ⅲ(理)23题的解法探究
2020-12-15 01:40:06广东省广州市铁一中学511447
中学数学研究(江西) 2020年12期
广东省广州市铁一中学 (511447) 范 群
1 试题呈现

2 试题证明
首先证明第(1)题:
证法1:因为a+b+c=0,abc=1,可见a,b,c不全相等,a,b,c均不为零,a,b,c中一正两负,不妨设a

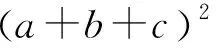
证法4:构造三次函数y=f(x)=(x-a)(x-b)(x-c),不妨设y=f(x)=(x-a)(x-b)(x-c),即y=f(x)=x3-(a+b+c)x2+(ab+bc+ca)x-abc=x3+(ab+bc+ca)x-1,显然,f(x)在[a,b],[b,c]上均满足罗尔定理的条件,由罗尔定理知f′(x)在(a,b)中至少一个零点,在(b,c)中至少一个零点,可见,f′(x)一共至少两个零点,而f′(x)=3x2+(ab+bc+ca),令f′(x)=0,显然当且仅当ab+bc+ca<0时,f′(x)最多有两个零,此时必有ab+bc+ca<0.
现证明第(2)题:


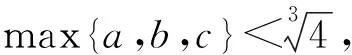
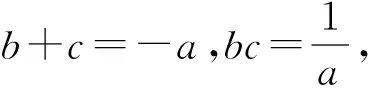

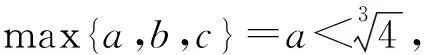
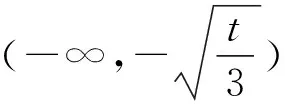

猜你喜欢
中学数学研究(2024年3期)2024-04-05 16:02:32
天府数学(2020年3期)2020-09-10 19:53:46
河北理科教学研究(2020年1期)2020-07-24 08:14:34
数理化解题研究(2020年13期)2020-05-07 03:29:02
数学物理学报(2019年5期)2019-11-29 07:46:30
高中生·天天向上(2016年9期)2016-11-22 09:10:34
数学学习与研究(2016年1期)2016-07-04 13:18:37
科普童话·百科探秘(2014年7期)2014-08-07 01:41:31
故事大王(2014年2期)2014-02-20 01:48:37
幸福家庭(2013年7期)2013-04-29 00:44:03

