例谈圆锥曲线中最值问题的解题方法
2020-12-15 01:40:22江苏省句容中等专业学校212400
中学数学研究(江西) 2020年12期
江苏省句容中等专业学校 (212400) 赵 林
最值问题是圆锥曲线中的常见题型,也是历年高考的热点之一.解决这类问题需要涉及到代数、几何、三角等相关知识,对培养学生的思维能力具有重要的作用.下面,笔者将圆锥曲线中最值问题的常见解法进行总结,与读者交流.
一、用定义法求最值
例1 已知AB是抛物线x2=4y的一条弦,且|AB|=6,求弦AB的中点M到x轴的最短距离.

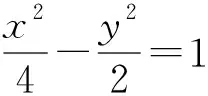
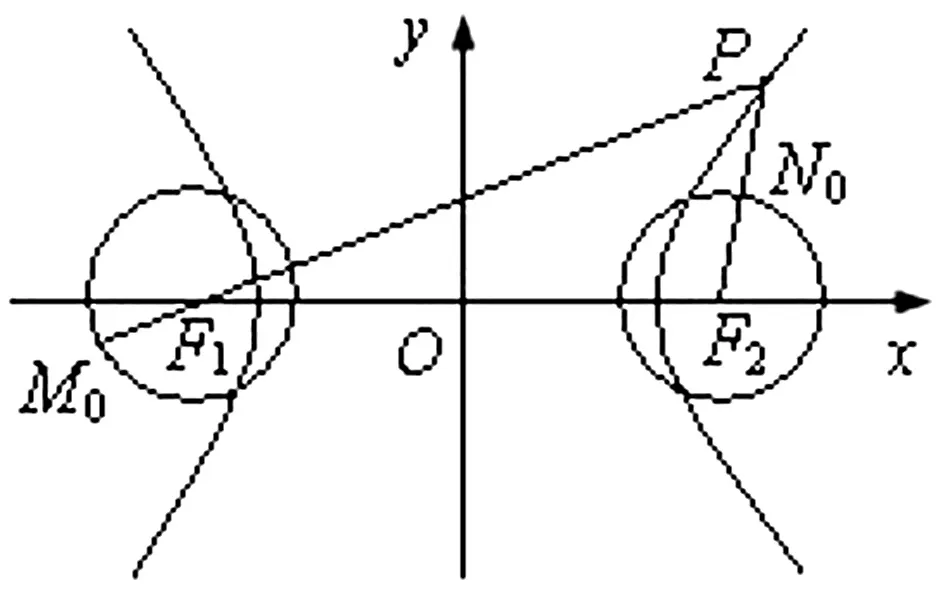
图1
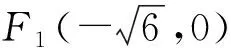
评注:利用圆锥曲线的定义,寻找条件和结论之间的内在联系,再结合平面几何的有关知识,可使解题简洁明快,得心应手.
二、用参数法求最值

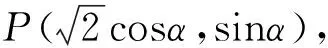
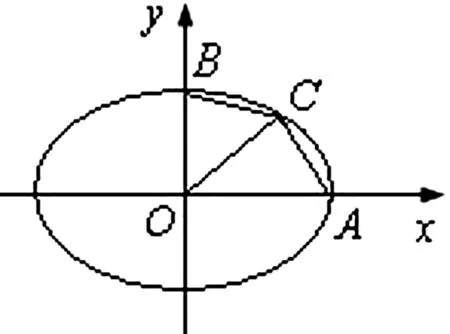
图2
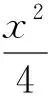
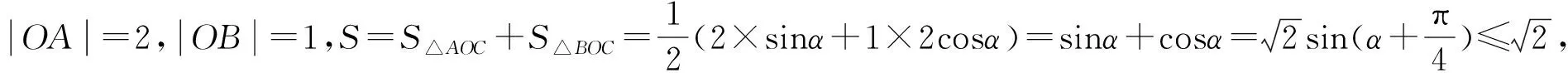
评注:参数法是联系代数和几何的桥梁,巧设椭圆的参数方程来解题,能达到化繁为简,开拓思路,快速解题的目的.
三、用函数方法求最值
例3 已知直线y=x+m与椭圆x2+3y2=6交于A,B两点,O为坐标原点,求△AOB面积的最大值.
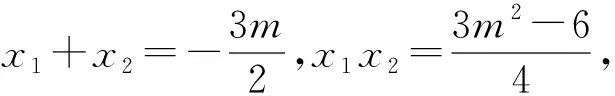
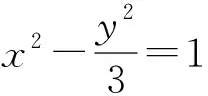
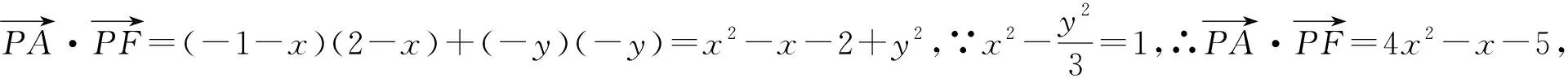
评注:函数方法是解决圆锥曲线中最值问题的常用手段,解题的关键是根据条件建立目标函数,从而使问题得到转化.
四、用均值不等式求最值
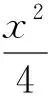
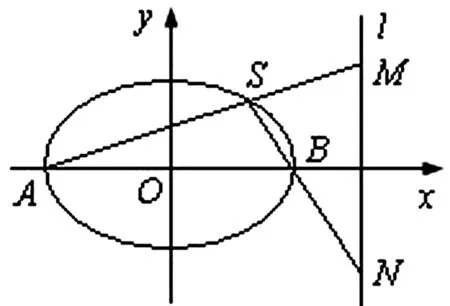
图3

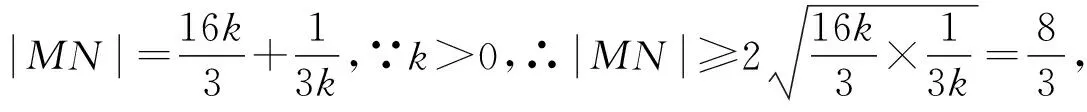
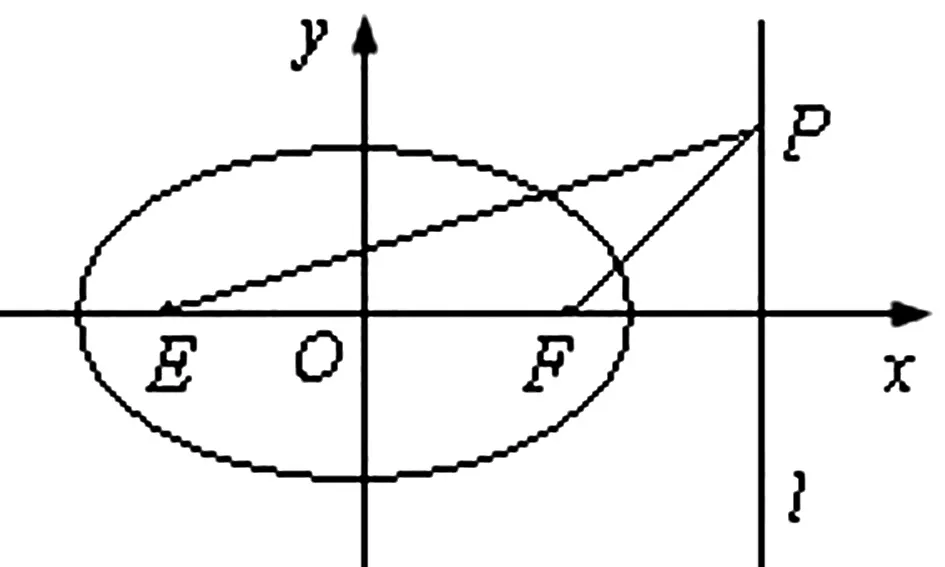
图4


评注:求圆锥曲线中的最值问题,要熟练地掌握圆锥曲线的定义和性质,灵活运用函数、不等式以及数形结合等思想方法,仔细审题,深刻挖掘隐藏条件,从而找到最恰当的解法.
猜你喜欢
数学杂志(2022年5期)2022-12-02 08:32:10
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26 14:03:32
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26 13:59:58
中学生数理化(高中版.高二数学)(2021年12期)2021-04-26 07:43:38
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08 01:28:48
河北理科教学研究(2020年3期)2021-01-04 01:49:38
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15 22:17:33
河北理科教学研究(2020年1期)2020-07-24 08:14:28
中学数学杂志(2019年1期)2019-04-03 00:35:42
高中生·天天向上(2017年2期)2017-06-09 06:38:14

