例谈“设而不求”在导数问题中的应用

江苏省常州市武进区前黄中学国际分校 (213161) 陆 德

在导数相关问题中许多问题都涉及到繁杂的运算,为了尽可能减少计算量,一些常用技巧和方法尤为必要，“设而不求”即是如此.所谓“设而不求”是指根据题设条件，巧妙设元，搭建＂未知＂和＂已知＂之间的等量关系, 通过合理代换或推理，利用整体化归，韦达定理，整体消元等方法化繁为简、避重就轻,“设而不求”在数据的处理上另辟蹊径，旨在条件的分析转化.

题型一 利用韦达定理消元

例1 (2017江苏高考)已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值，且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)

(1)求b关于a的函数关系式，并写出定义域；

(2)证明：b2>3a；

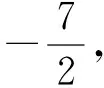
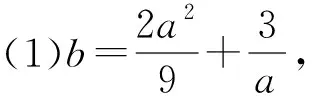
评注：如果孤立看待x1,x2，则需借助于求根公式，显然求解f(x1),f(x2)时运算过于繁琐，而通过韦达定理寻求两者关系后，运算f(x1)+f(x2)过程就浅显明朗.

题型二 整体换元实现消元

例2 (盐城市2019届高三第三次模拟考试)设函数f(x)=x-aex(e为自然对数的底数，a∈R)．

(1) 当a=1时，求函数f(x)的图象在x=1处的切线方程；

(2) 若函数f(x)在区间(0,1)上具有单调性，求a的取值范围；

解析：(1)略；(2)略；(3)函数g(x)=(ex-e)f(x)的零点即为方程(ex-e)f(x)=0的实数根，故ex-e=0或f(x)=0，由ex-e=0，得x=1，

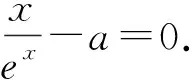
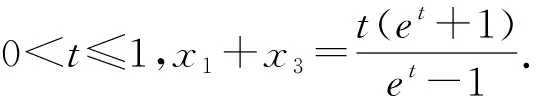
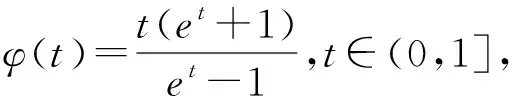
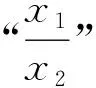
题型三 虚设零点整体替换

例3 (2020届常州市第一学期期中考试)已知函数f(x)=lnx-xex+ax(a∈R).

(1)若函数f(x)在[1,+∞)上单调递减，求实数a的取值范围；

(2)若a=1，求f(x)的最大值.

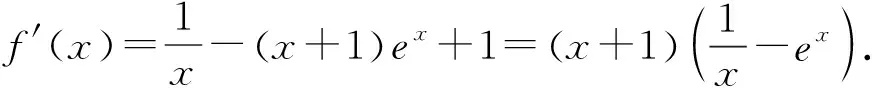
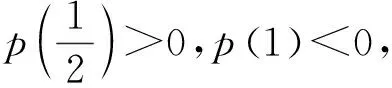
评注：在解决函数和导函数的综合问题中，导函数的零点确定存在但无法直接求解时，可以结合零点存在定理虚设零点，巧妙利用零点所满足的等量关系推理演算整体代换，复杂问题从而迎刃而解.

“设而不求”是高中数学解题的常用方法,也是实际应用中的难点，其实质是整体结构意义上的变式和整体思想的应用,数据的整合加工处理过程中利用转化与化归思想，从形式和结构上提炼内核，转化到常规知识背景下，从而将目标清晰化，问题简单化.