简单多面体的内切球与外接球问题解题基本方法

◇ 甘肃 杨子林

(作者单位:甘肃省张掖市第二中学)

简单多面体的外接球和内切球问题是每年高考的热点问题,其解题的关键在于确定球心在多面体中的位置,找到球的半径或直径与多面体相关元素之间的关系,结合原有多面体的特性求出球的半径.

1 简单多面体的内切球半径

求简单多面体内切球半径利用体积分割法,这与求三角形内切圆的半径的方法(面积分割法)类似.求三角形内切圆的半径需要把内心与三个顶点分别相连,把三角形分割为三个小三角形,则c)r,因此

求多面体内切球的半径用体积分割法.把多面体内切球的球心与各顶点相连,则将该多面体分割为n个棱锥,设这n 个棱锥的底面面积分别为S1,S2,…,Sn,多面体的表面积为S,内切圆半径为r,于是

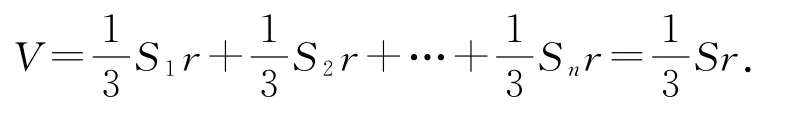
例1在四棱锥P-ABCD 中,底面ABCD 是边长为a 的正方形,PD ⊥底面 ABCD,PD ＝a,PA ＝若在这个四棱锥内放一球,求此球的最大半径.

设此球半径为R,最大的球应与四棱锥各个面相切,设球心为S,连接SA,SB,SC,SD,SP,把此四棱锥分为5个棱锥,设它们的高均为R.

2 简单多面体的外接球球心位置

简单多面体的外接球问题比较复杂,解题关键是确定外接球的球心的位置,本文介绍确定简单多面体的外接球的球心位置的三个基本方法.

1)定义法

一些特殊的几何体(如正方体、长方体等)可利用几何体的性质确定球心的位置.

例2在矩形ABCD 中,AB＝4,BC＝3,沿AC将矩形折成一个直二面角B-AC-D,求四面体ABCD的外接球的体积.

根据直角三角形斜边的中线等于斜边的一半,外接球球心是对角线AC 的中点,因此球的半径是则球的体积为

2)性质法

利用球心O 与截面圆圆心O′的连线垂直于截面圆、球心O 与弦中点的连线垂直于弦、弦的垂直平分面必过球心的性质确定球心的位置.

例3如图1,球面内接三棱锥P-ABC,PA⊥平面ABC,PA＝2,△ABC 是边长为的正三角形,求球面的面积.

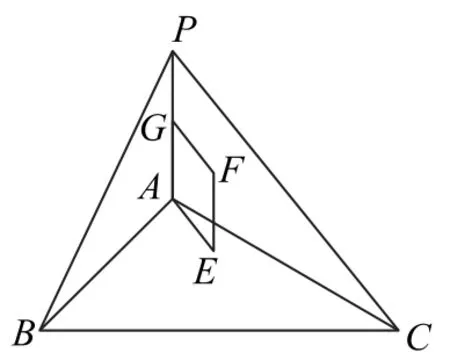
图1

取△ABC 外接圆的圆心为E,△ABC 的外接圆就是外接球的一个轴截面圆,因为截面圆的圆心与球心的连线垂直于截面圆,与弦PA 的垂直平分面相交于点F,则四边形AEFG 为平行四边形.△ABC 的外接圆半径为AE＝1,AG ＝1,外接球的半径为 AF,则 AF2＝故球面的面积为8π.

3)补形法

同一顶点处的三条侧棱两两垂直的四棱锥补形为长方体,正四面体补形为正方体,对棱相等的四面体补形为长方体.

例4设三棱锥P-ABC 中则该三棱锥外接球的半径为________.

一般地,对棱相等的四面体补形为长方体,长方体相对面的对角线长度相等,所以以相等的对棱当作长方体相对面的对角线将其补成长方体.设长方体的一个顶点上的三条棱长分别为x,y,z,则即x2＋y2＋z2＝50,四面体外接球的半径为