基于AMESim的装载机换挡冲击影响因素的研究与优化

范久臣， 孙雪梅

(北华大学 机械工程学院， 吉林 吉林 132021)

引言

装载机是一种常用的非公路工程机械，具有机动性强、工作效率高和易操作等优点，使用范围较广[1]。装载机作业工况多采用V，I，L，T型循环作业，工作过程中，换挡频率较高，每小时换挡次数近千次，因此换挡品质的高低对装载机的驾驶舒适性、使用寿命及作业效率有至关重要的影响。目前，国内大部分装载机的行走传动系统核心部分均采用液力变矩器配合动力换挡变速箱组合形式，通过操纵换挡缓冲阀控制变速箱挡位离合器的结合与分离实现挡位的切换。装载机变矩器的输出特性及离合器的扭矩传递特性对换挡品质有着重要的影响，车辆在换挡过程中，由于惯性会传递给装载机巨大的反作用转矩，以及离合器内油温动态上升使得摩擦元件间传递的力矩伴有一定的转矩波动，从而引起换挡冲击[2]。

现阶段，国内外学者、研究机构对换挡品质的影响因素进行了大量的研究。其中，YANG Shujun等[3]研究了动力换挡过程中流体空气含量对液压-机械变速传动动态特性的影响规律，建立了流体机械变传动中液压回路功率转移的数学模型，并在MATLAB/Simulink中进行了仿真，可以有效降低冲击波动。OH, JY等[4]对某装载机自动变速器传动系统进行了建模分析，并在此基础上对其换挡质量进行了分析，通过比较相同工况下的试验和仿真结果，验证了装载机动力传动系统的分析模型。

在国内，邹宏等[5]结合ZL50装载机传动系统,并针对液压控制的动力换挡离合器在换挡时传递转矩变化,总结了换挡品质的几个主要影响因素;用MATLAB/Simulink对评价指标中的冲击度进行仿真分析,最后通过试验验证给出实现改善的控制策略。刘建民等[6]对变速器换挡控制与换挡品质进行了研究，提出了一种新的旨在提高换挡品质的变速器换挡控制策略，能够有效地降低换挡过程中产生的冲击，提高了车辆的平顺性。夏光等[7]利用极小值最优控制原理求解换挡过程的最优控制量，实现大功率拖拉机动力升挡的最优控制，并利用MTALAB/Simulink进行建模与仿真，控制策略能够实现较小的滑磨功，在保证动力性能不降低的前提下大大减少离合器的滑磨损失。汪小芳等[8]针对负载敏感系统主阀瞬时启闭出现的液压冲击问题，利用AMESim建立了负载敏感液压系统防冲击的仿真模型，表明了系统冲击与负载压力无关，且系统冲击压力随着流量的增加而不断升高。夏扩远等[9]对拖拉机中的动力换挡模块进行建模，建立动力学方程，并利用MATLAB/Simulink平台提出基于发动机反馈协调控制的动力换挡策略，该策略能够有效减小速度的损失和减小车辆冲击度。李阳等[10]基于AMESim建立了电驱动桥换挡控制仿真模型，并与Simulink控制策略进行联合仿真验证，所制定的控制策略缩短了换挡时间，降低了换挡冲击，有效地改善了换挡品质。朱镇等[11]对分段式液压机械无级变速器建立仿真模型，并对其换挡策略进行仿真分析，通过实验验证了优化物理参数和换挡时序，有效提升了变速器的换挡品质。施琪等[12]对一种换挡缓冲阀运用AMESim进行了建模，并进行了仿真分析和试验验证，分析了压力瞬时波动及流量瞬时波动对缓冲效果的影响。高翔等[13]针对一种液压机械无级变速器的换挡策略进行仿真分析和试验验证，发现发动机转速、调速阀流量、主油路油压以及负载转矩是影响换挡品质的主要因素。席志强等[14]研究了换挡过程动态特性分析方法，引入变速器输出转速和输出转矩作为拖拉机生产率和动力性的评价指标，运用动力学原理构建动力换挡变速器模型，确定了动力换挡变速器换挡品质的控制方法及控制策略，提高了换挡品质。

本研究在前人的研究基础上，以某型号装载机行走传动系统为研究对象，对其换挡过程中的动力传递特性进行分析，利用AMESim软件建立该型装载机行走传动系统的仿真模型，通过仿真分析与实验测试，研究离合器充油压力及液力变矩器扭矩变化对装载机换挡品质的影响，并针对换挡冲击提出优化方案。

1 换挡过程及其评价指标

1.1 换挡过程

车辆的换挡本质是改变整个传动系统的传动比，使发动机输出特性更好地适应外负载变化。换挡前后传动比发生改变，由于装载机整机质量大，加减速过程存在极大的动载荷，变速箱输入端与输出端的转速、转矩无法立刻适应新的转速比，从而导致换挡冲击。图1为某型号装载机动力传动简图。

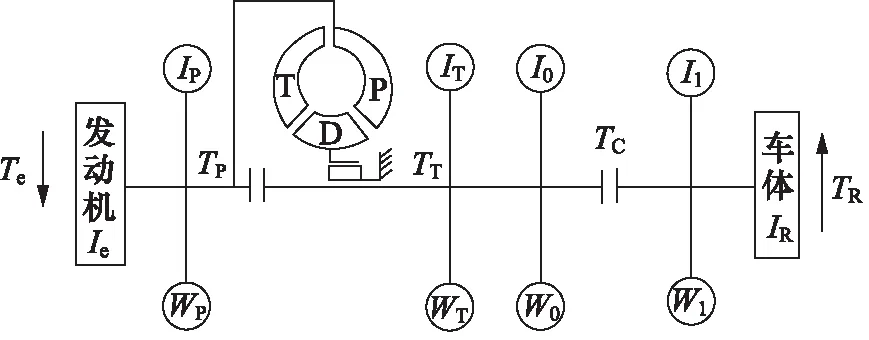
图1 装载机动力传动系统简图

以车辆一挡起步为例分析换挡过程。起步时，换挡操纵阀控制一挡离合器油路接通，离合器充油压力不断升高。离合器摩擦片的间隙随着充油压力的增大而减小，直至完全贴合。主、从动摩擦片受压滑转，离合器传递扭矩的能力也随着摩擦片间隙的减小而逐渐升高，主动片转速逐渐下降，从动片转速逐渐升高，同时离合器伴随着二者的转速达到相同而停止滑磨，完成换挡过程。

离合器传递的扭矩是随着离合器上的油压变化而变化的，离合器所能传递的摩擦扭矩的计算公式为：

M=nμpRPk

(1)

式中，n—— 摩擦面数，n=s+t-1(其中，s为主动片数;t为从动片数)

μ—— 摩擦面间的摩擦系数，湿式，粉末冶金钢，取μ=0.08

p—— 摩擦面上的总轴向压力

RP—— 平均半径，一般取RP=(R外+R内)/2

k—— 折减系数。湿式，摩擦面数为10，取k=0.95

液力变矩器作为系统中的柔性部件，不仅可以缓冲来自发动机的扭矩脉动，而且还可以提高传动系统的瞬时扭矩，以提高车辆启动特性。液力变矩器的无因次特性模型如下：

(2)

式中,i=nT/nB—— 液力变矩器转速比

nT—— 涡轮转速

nB—— 泵轮转速

λB—— 泵轮转矩系数

K—— 液力变矩器变矩系数

η—— 液力变矩器的效率

本研究所采用的液力变矩器的无因次特性曲线如图2所示，由此得液力变矩器的输出扭矩计算公式：

(3)

式中,MB—— 变矩器泵轮扭矩

ρ—— 变矩器油密度

g—— 重力加速度

D—— 循环圆直径

1.泵轮转矩系数 2.变矩系数 3.变矩器效率图2 液力变矩器无因次特性曲线

1.2 换挡品质评价指标

换挡品质的好坏主要体现在：换挡过程中车速变化的平顺性，换挡时间(即离合器滑磨时间的长短)，传动系零部件载荷波动的大小。

目前，由于工程车辆的作业工况复杂，其换挡品质尚无合适的评价指标，在评价时还只是参考普通汽车的换挡品质评价指标。换挡品质一般用冲击度作为评价指标，其数学表达式为：

(4)

式中，J—— 冲击度

v—— 车速

t—— 时间

rr—— 车轮的滚动半径

IW—— 变矩器之后传动系统等效惯量

i0—— 主减速比

T0—— 变速器输出转矩

TW—— 车轮的阻力矩

因此，为了确定动力换挡过程中换挡品质的影响因素，需要根据换挡过程原理、传动系统元件主要参数以及样机实际尺寸等搭建相应的AMESim模型。

2 AMESim模型搭建

由于装载机轮胎与地面的接触情况较多，所以装载机样机传动系统是一个比较复杂的闭式系统，便于合理建模需对传动系统的工作状态进行相应的简化：

(1) 装载机行驶过程中整车只考虑受纵向力；

(2) 忽略装载机各类轴、轴承座与轴承以及齿轮啮合之间的横向弹性振动；

(3) 需将传动系统假设为是一个无惯性的弹性环节和无弹性的惯性环节组成质量系统；

(4) 忽略传动系统的各项无关间隙与阻尼。

根据上述简化，建立装载机样机传动系统的AMESim仿真模型。模型主要有：图3所示的变速操控系统；图4所示的发动机、液力变矩器和变速箱模型；图5所示的驱动桥、轮胎地面负载系统。其中，发动机与液力变矩器模型直接采用AMESim Powertrain模块中的子模型。图3变速箱操纵阀的控制端口与图4中的液力变矩器控制端口对应相连，变速箱输出口EX与图5驱动桥的输出口IN连接。

仿真模型中各个元件的参数主要根据结构实际测绘及实际工况来设定，其中装载机行走系统模型部分关键参数见表1所示。

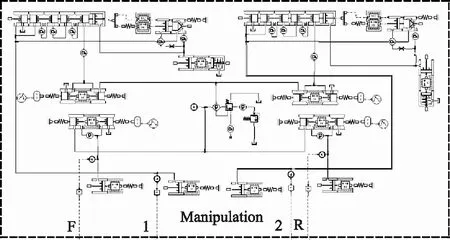
图3 变速操控系统图

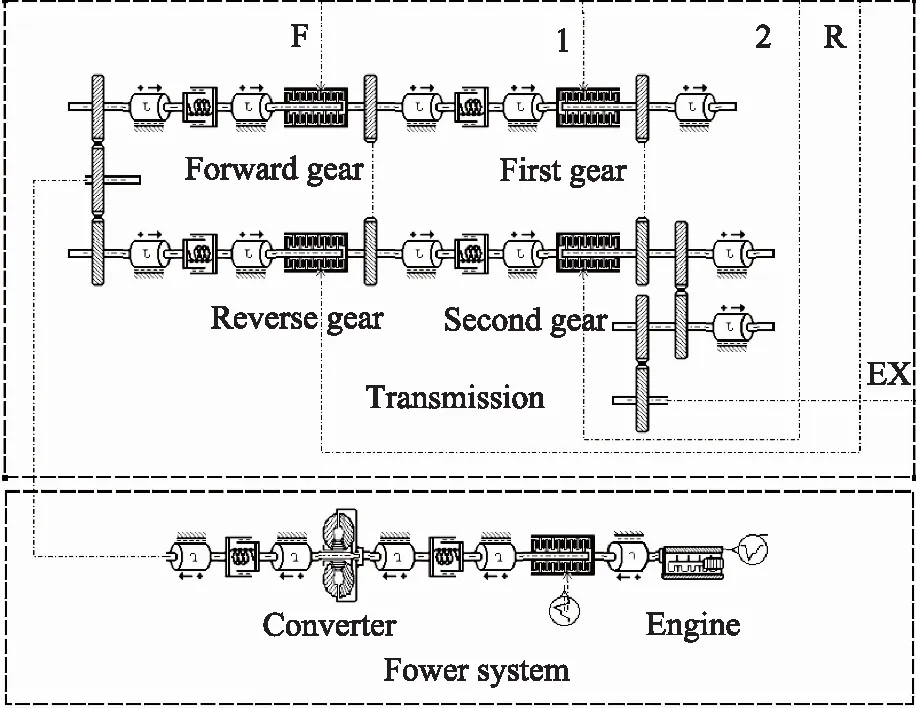
图4 发动机、液力变矩器和变速箱

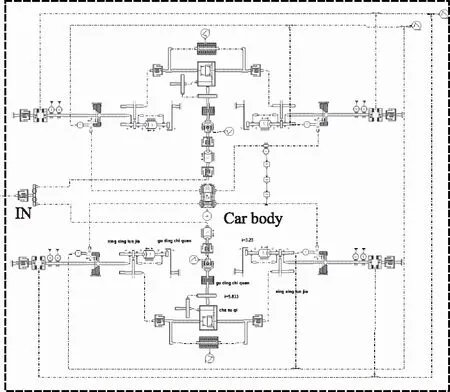
图5 驱动桥、轮胎地面负载系统

3 传动系统实验与仿真分析探索

根据分析所需，实验方案主要测量液力变矩器涡轮、发动机的转速，一挡离合器的充油压力和变速操纵阀口压力以及离合器的传递扭矩。结合样车结构，实验测点布置如图6所示。

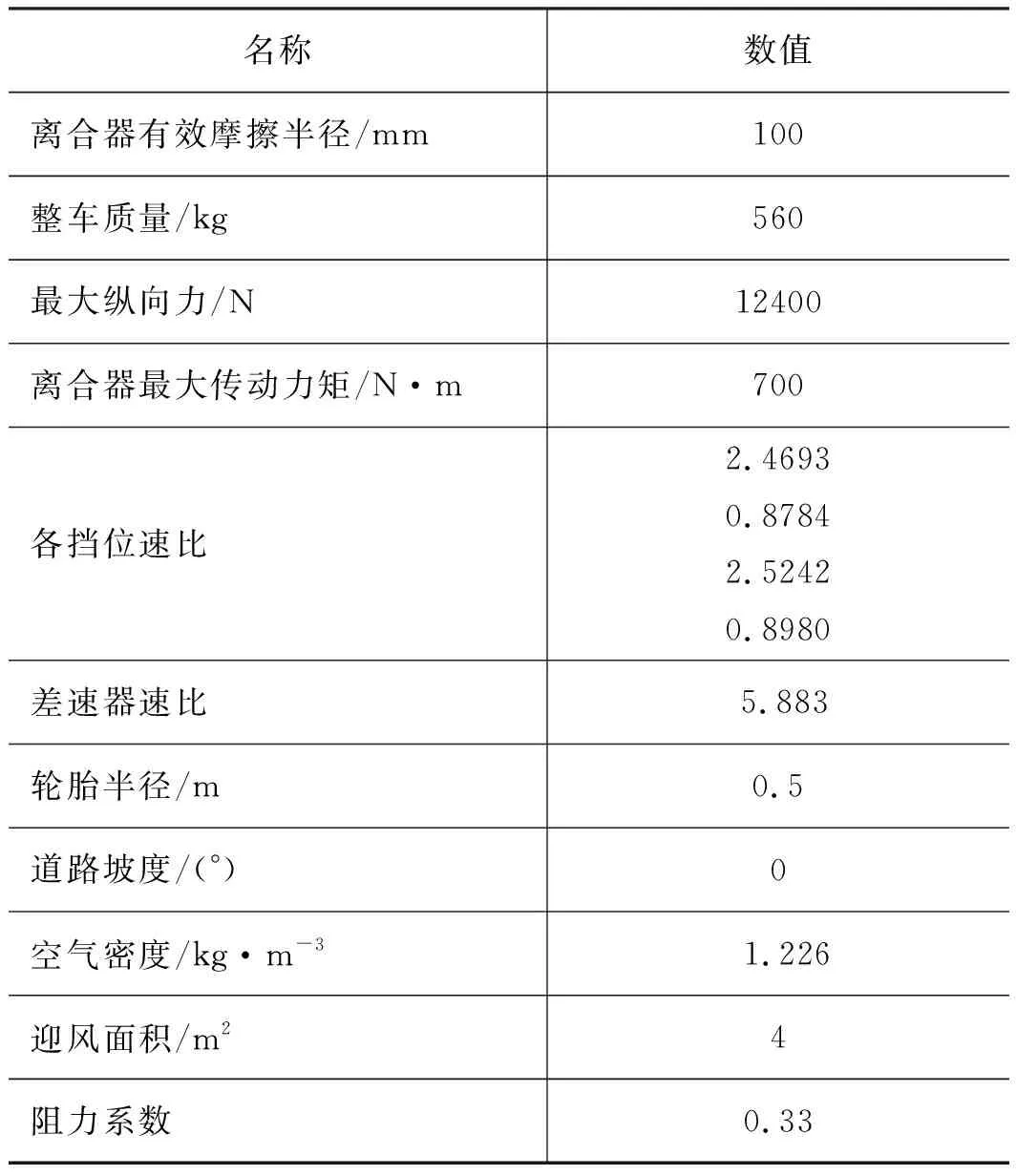
表1 传动系统仿真模型主要参数设置

图6 实验测点布置图

3.1 仿真模型验证

车辆由静止状态到运动状态，针对装载机换挡时，发动机处于额定转速状态。在换挡过程中，实验装载机样机一挡离合器的充油压力特性曲线如图7所示，由于换挡冲击而形成的冲击度特性曲线如图8所示。

对比图9和图10的运用AMESim软件对一挡离合器的充油压力和车辆冲击度所做的仿真曲线，可得一挡离合器的充油压力特性仿真曲线与实验压力值曲线、车辆的冲击度特性仿真曲线与实验样机冲击度曲线均形状相似趋势相近，具有高度一致性，仿真与实验结果基本相符， 即仿真模型准确可靠。误差产生是主要原因是由于仿真当中只考虑车辆在路面行驶时所受的纵向力，而忽略动力系统及传动系统自身的震动，因此仿真曲线较实验曲线光滑，仿真曲线中车辆冲击度恢复稳定所用时间较短，响应频率高，且数值略小于实验测得的冲击度。

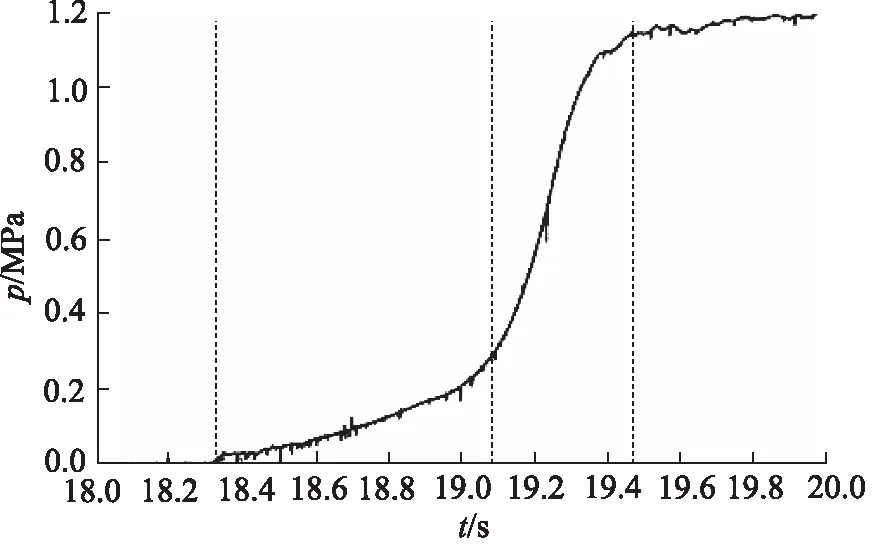
图7 一挡离合器充油压力变化

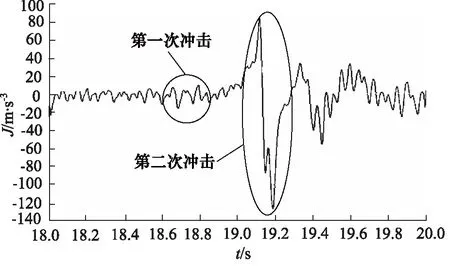
图8 实验样机冲击度

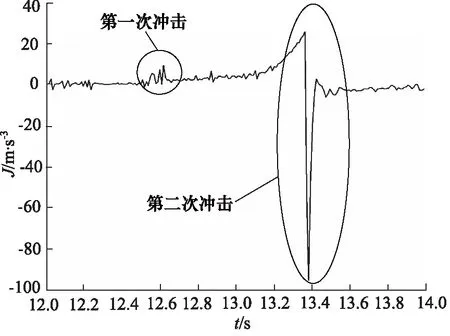
图10 仿真车辆冲击度

3.2 车辆冲击度特性仿真分析

接下来分析产生两次冲击的原因。相同工况设置条件下对模型的一挡离合器充油压力与整车冲击度进行仿真分析。仿真结果如图9和图10所示。

仿真结果显示：一挡离合器充油压力起始于12.2 s，到14 s时趋于稳定；换挡过程中有两次冲击发生，第一次位于12.5～12.7 s之间，第二次冲击位于13.2～13.4 s之间，同样是第一次冲击比较小，第二次冲击比较大。

仿真曲线分析，在换挡过程中产生两次换挡冲击产生的原因：第一次冲击是由车辆由静止状态到运动状态的转变造成的。由图10冲击度曲线和图12离合器主从动转速曲线可以看出，第一次冲击位于12.6 s，此时离合器从动片开始转动。

第二次冲击是由离合器结合之后扭矩突然下降导致的，从图12可以看出在13.4 s，离合器停止滑磨，变矩器涡轮转速状态发生改变，变矩器输出扭矩突降，同时产生冲击。

1.离合器传递扭矩能力 2.离合器实际传递扭矩图11 离合器传递扭矩能力与离合器实际传递扭矩

3.3 离合器传递扭矩、转速特性分析

由式(1)可知，当变速箱离合器确定后，离合器瞬时传递扭矩的能力与摩擦面上的瞬时总轴向压力p成正比，因此通过控制压力p就可以控制离合器传递扭矩能力。在换挡过程中，离合器传递扭矩能力与离合器实际传递扭矩特性曲线如图11所示。由图11可知，离合器传递扭矩能力随着离合器充油压力的升高从0上升到830 N·m，在12～13.4 s之间，离合器实际传递扭矩与离合器传递扭矩能力相同，在13.4 s之后离合器实际传递扭矩不再与离合器传递扭矩能力有关，因此可以判断在13.4 s时离合器停止滑磨。

同时，对液力变矩器涡轮和发动机的转速、离合器传递扭矩以及离合器从动片转速除传动比作仿真运行，得到图12的特性曲线。从图12可以看出，换挡起始阶段，主动片处在最高转速，从动片静止，随着离合器充油压力的升高离合器传递扭矩能力逐渐升高，主动片转速逐渐下降，从动片转速逐渐升高，在13.4 s时主、从动片转速相同，离合器停止滑磨。

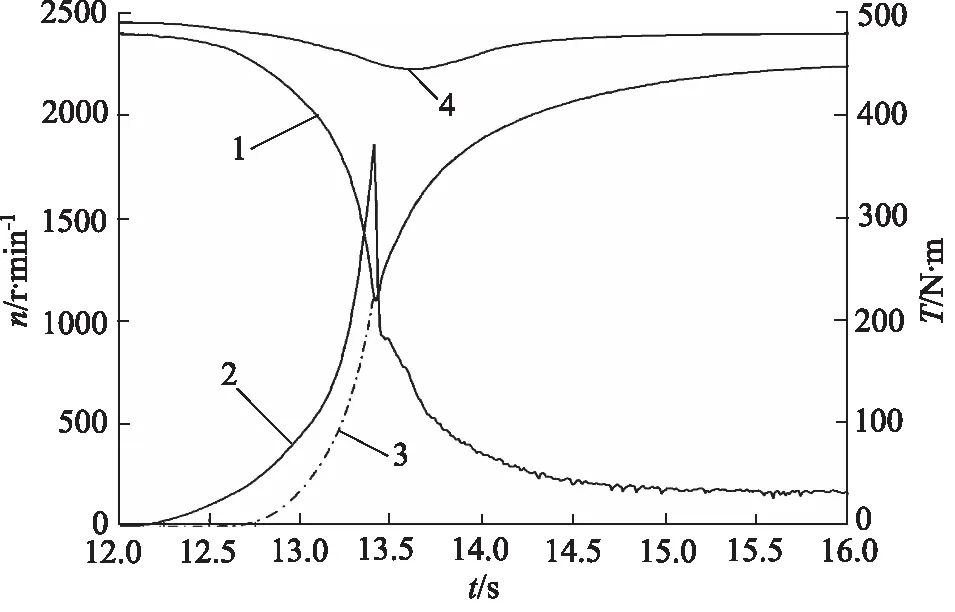
1.液力变矩器涡轮转速 2.离合器传递扭矩3.离合器从动片转速除传动比 4.发动机转速图12 变矩器、离合器转矩、转速特性曲线

换挡过程中，离合器实际传递扭矩取决于车辆动力性能与离合器实际传递扭矩能力。当离合器传递扭矩能力低于此转速下动力系统产生的最大扭矩时，离合器实际传递扭矩为离合器所能传递的扭矩最大值；当离合器此时传递扭矩能力高于此时车辆动力系统所能产生的最大扭矩时，离合器不再滑磨，此时的离合器相当于联轴器。

发动机与液力变矩器的共同输出特性决定了车辆在换挡过程中会有1个最大扭矩点，从图12仿真结果中可以看出最大扭矩值出现在13.4 s。13.4 s之前，动力系统会通过降低速度来增加扭矩，以使车辆获得足够的加速度，完成速度的提升，离合器从动片的转速随着变矩器涡轮的转速下降而升高，离合器处于滑磨阶段，此时离合器传递扭矩大小取决于离合器总轴向压力p；13.4 s之后，离合器停止滑磨，主、从动片转速同时升高，动力系统开始进入升速降扭阶段，输出扭矩减小。13.4 s时，涡轮工作状态发生改变,从降速状态转变到升速状态，由液力变矩器特性曲线可知，此转变将导致液力变矩器输出扭矩突降，从而使得瞬时加速度突然减小，进而产生了较大的冲击。

由液力变矩器输出扭矩式(3)可知，当选定液力变矩器及液力变矩器用油后，液力变矩器的输出扭矩与变矩系数k、泵轮转矩系数λB及泵轮转速nB正相关，变矩系数k、泵轮转矩系数λB为转速比i的函数。从图12中仿真结果可以看出，变矩器输出扭矩突降点即为离合器结合点，在离合器结合点附近泵轮转速曲线斜率变化较小，而涡轮转速曲线斜率变化较大，变矩器转速比变化率较大，因此在分析离合器结合点附近变矩器输出扭矩时，为了简化分析，可以将泵轮转速设为定值，只分析转速比对变矩器输出扭矩的影响。从液力变矩器特性曲线图2可以看出：变矩系数k与转速比呈负相关；在转速比大于0.45时，泵轮转矩系数λB与转速比呈负相关，转速比小于0.45时，呈正相关。

从图12中可以看出在离合器结合点附近转速比大于0.45，因此在离合器结合前，随着离合充油压力的升高，变矩器涡轮端负载增大，转速下降，转速比减小，变矩系数k、泵轮转矩系数λB均增大，变矩器输出扭矩增大；在离合器结合后，涡轮转速升高，转速比增大，变矩系数k、泵轮转矩系数λB均减小，输出扭矩减小。因此在离合器结合时变矩器输出扭矩大小与变矩器转速比呈正相关，动力系统扭矩突变值的大小取决于离合器结合前后变矩器转速比变化率，变矩器转速变化率越小，液力变矩器产生扭矩变化越小。

转速比变化率与发动机的外特性和涡轮上的负载特性有关。离合器完全结合前，涡轮上的负载形式主要为离合器端的扭矩负载，此时转速比变化率取决于离合器充油压力变化的斜率，离合器压力变化斜率越小，转速比越小；在离合器完全结合后，负载形式为车辆惯性负载，此时转速比变化率由车辆的加速度决定，而离合器刚结合的瞬间车辆加速度的大小与离合器结合时压力值的大小呈正相关，因此可以通过调整离合器充油压力来减小离合器结合前后转速比变化率，从而减小换挡冲击。

综合上述分析得出，离合器结合时压力值越小，结合前压力变化率越小，越有助于换挡品质的提高；但离合器充油压力越小，车辆加速度就越小，车辆完成加速所需的时间就越长，离合器滑摩时间也越长。

4 冲击问题优化及结果分析

综合考虑各项因素，通过调整换挡缓冲阀，改变离合器结合前充油压力变化率，对样机传动系统进行优化改进。改进后的离合器充油压力实验测试曲线如图13所示，样机冲击度曲线如图14所示。

图13 调整后离合器充油压力

图14 调整后实测样机冲击度

对比图13和图7可以看出，改进后离合器的充油压力从0增长至0.6 MPa的时间由1 s变成2 s，且增长率逐渐减小；0.6 MPa增长至1.2 MPa的时间由0.2 s 变成0.5 s。对比图14和图8可以看出，改进后在离合器停止滑磨，变矩器涡轮转速状态发生改变时，样机的冲击度由(-120,80)降到了(-25,30)。即按上述结论调整离合器的充油压力增长率后，车辆换挡时的冲击明显减小，换挡也更为平稳，换挡品质明显提高。

综合以上分析可以看出，转换过程中共有2个冲击点，第1个冲击点是由车辆由静止状态到运动状态的转变造成的；第2个冲击点是由离合器结合之后扭矩突然下降导致的。离合器结合时压力值越小，结合前压力变化率越小，越有助于换挡品质的提高；但离合器充油压力越小，车辆加速度就越小，车辆完成加速所需的时间就越长，离合器滑摩时间也越长。

根据前面的分析，传动系统扭矩突降值的大小与扭矩突变前后液力变矩器涡轮、泵轮转速比变化率呈正相关。转速比变化率与离合器充油压力和车辆惯性有关：离合器结合之前，转速比变化率取决于发动机外特性和离合器充油压力变化的斜率，离合器充油压力变化斜率越小，转速比越小；在离合器结合时，转速比变化率取决离合器结合时车辆加速度，车辆加速度越小，转速比越小。结合实验测试结果可以得出，通过调整换挡缓冲阀，改变离合器结合前充油压力变化率可以降低整机冲击度，从而改善换挡品质。

5 结论

本研究依据机理分析以及仿真实验相结合的研究方法，分析了离合器充油压力和液力变矩器的转速变化率对装载机换挡品质的影响，找出造成两次换挡冲击的根本原因和影响因素，并提出了改进方案，得到以下结论：

(1) 通过对装载机传动系统换挡过程的分析，从理论角度表明了换挡冲击主要由离合器的充油压力以及液力变矩器的特性引起的，液力变矩器涡轮的工作状态从降速状态转变到升速状态，此转变将导致液力变矩器输出扭矩突降，从而使得瞬时加速度突然减小，进而产生较大的冲击；

(2) 运用AMESim仿真软件建立了装载机样机行走传动系统的仿真模型，并通过实验测试验证了该模型的正确性。通过调整离合器充油压力来减小离合器结合前后转速比变化率来减小换挡冲击，改善了换挡品质，有效的解决了换挡冲击问题，为各类工程机械的液力传动系统开展虚拟设计与优化奠定了基础。