航材供需平衡调运问题优化研究
刘臣宇,李卫灵,孙伟奇 (海军航空大学 青岛校区,山东 青岛266041)
LIU Chenyu, LI Weiling, SUN Weiqi (Naval Aviation University Qingdao Campus, Qingdao 266041, China)
1 航材运输决策主要解决的两个方面问题
(1) 运输方式和运输路线的选择。在一对收发点之间存在着多种可供选择的运输方式及运输路线的情况下,以航材运输的安全性、及时性和低费用为目标,综合考虑、权衡利弊,选择合理的运输方式并确定适当的运输路线。
(2) 合理调运。在多个发货点和收货点之间组织一类或多类航材的运输活动时,考虑各种客观条件的限制,制定出合理的运输方案。
2 运输调运模型及其求解
(1) 调运模型
本文主要研究总供应量等于总需求量,称之为供需平衡运输问题。
假设某种航材有m个供应点,其供应量分别为ai(i=1,…,m);有n个需求点,需求量分别为bj(j=1,…,n)从第i个供应点向第j个需求点运送单位航材的运费为Cij,设Xij为从供应点i向需求点j运输航材的数量,F为运输总费用,则数学模型为:

(2) 模型求解
上述模型是一个线性规划模型,含有m×n个未知数,由平衡条件可将上述m+n个方程划为等价的m+n-1 个独立方程,可用单纯形法求解,但基于这类问题的特殊性,也可通过表上作业法求解。
表1 是一个供需平衡表,表上作业法是依据单位运价表在供需平衡表上进行迭代,确定最优方案。
既然运输问题是线性规划问题的特例,按照线性规划的解法是从m×n个变量先分离出m+n-1 个独立的变量(m+n个方程只有m+n-1 个独立方程)作为基变量,其它为非基变量进行迭代。运输问题的表上作业法也是基于这个思想,为此在供需平衡表中引入闭回路的概念。
所谓闭回路就是能排列成闭合回路的变量集合称。闭回路的每条边都是水平或垂直的,每个顶点是两条相互垂直边的相连点,每列(行) 若有顶点,必只有两个。有了闭回路的概念,根据线性规划求解的方法就可以确定m+n-1 个变量是否构成基的充要条件为:m+n-1个变量不含闭回路。根据这个思路,可确定初始调运方案。方法是:一个供应点的航材假如不能按最小运费就近供应,就考虑次小运费,这样就有一个差额,差额越大,说明不按最小运费调运时,运费增加越多,因此在差额最大处,就采用最小运费调运。从行差额或列差额中选出最大者,再对所选择的最大行(列) 差,选择其所在行或列中的最小运价元素,就可确定得到满足的需求点(或供应能力不足的供应点),去掉得到满足需求的列(或供应能力不足的行),对已划去的列(或行) 得到的新的供需平衡表,用同样的方法进行分配,最后可以得到初始调运方案。
得到初始调运方案后,要检验初始调运方案是否为最优调运方案,方法是应用位势法。即:应用σij=Cij-ui-vj(其中:σij为非基变量检验数,ui,vj为行和列的位势) 进行检验,当所有非基变量(供需平衡表中的空格) 检验数σij的值为正数时表明已得到最优解,否则再继续进行调整。
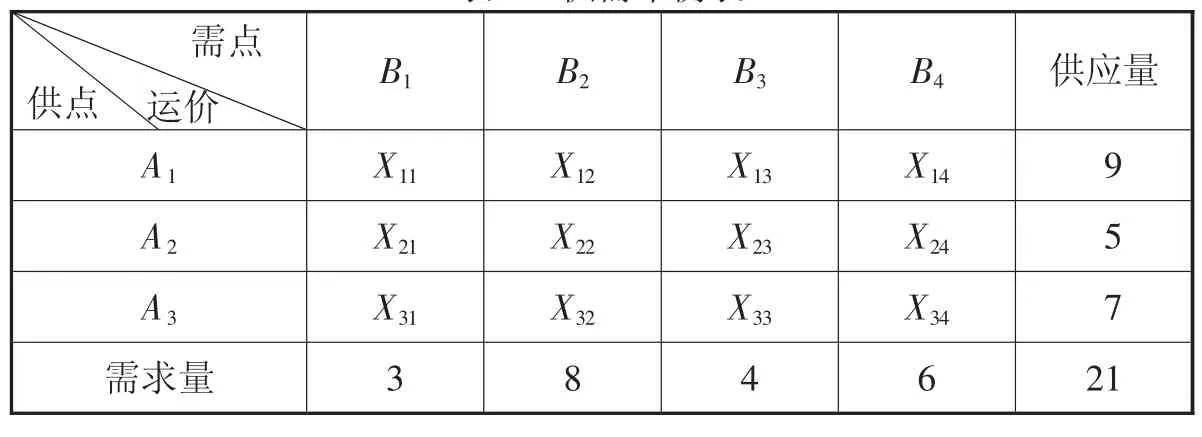
表1 供需平衡表
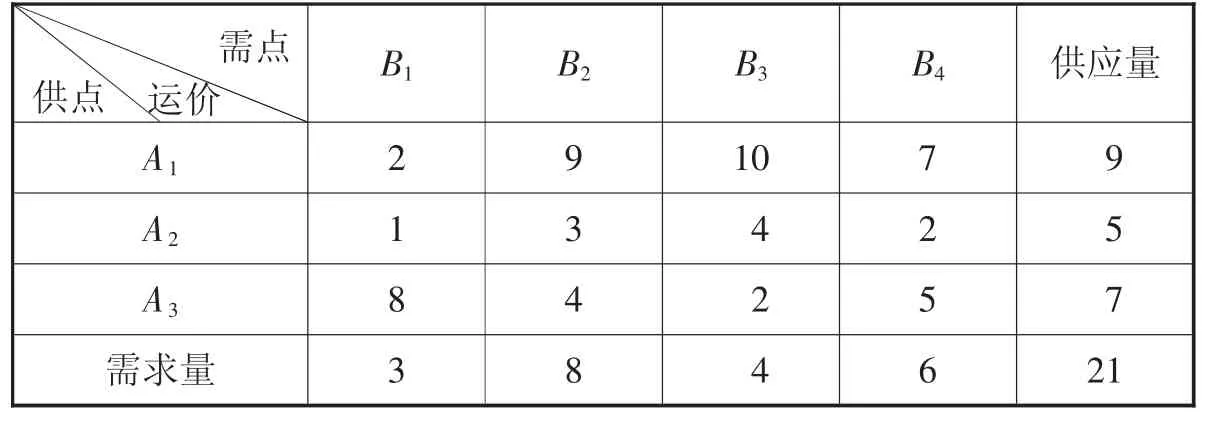
表2 单位运价表
3 模型应用
假设从3 个航材仓库组织货源发往4 个航材使用单位,航材仓库供应器材量与各航材使用单位需要量以及各地间单位航材运价见表2。Ai表示航材仓库,Bj表示航材使用单位。由表2 可以看出,这是一个供需平衡的调运问题。为了使运输费用最小,必须找出最优运输方案。
其步骤如下:
(1) 确定初始调运方案
第一步:在单位运价表中计算各行与各列的最小运费与次最小运费的差额,并填写在表的最右列和最下行,见表3。
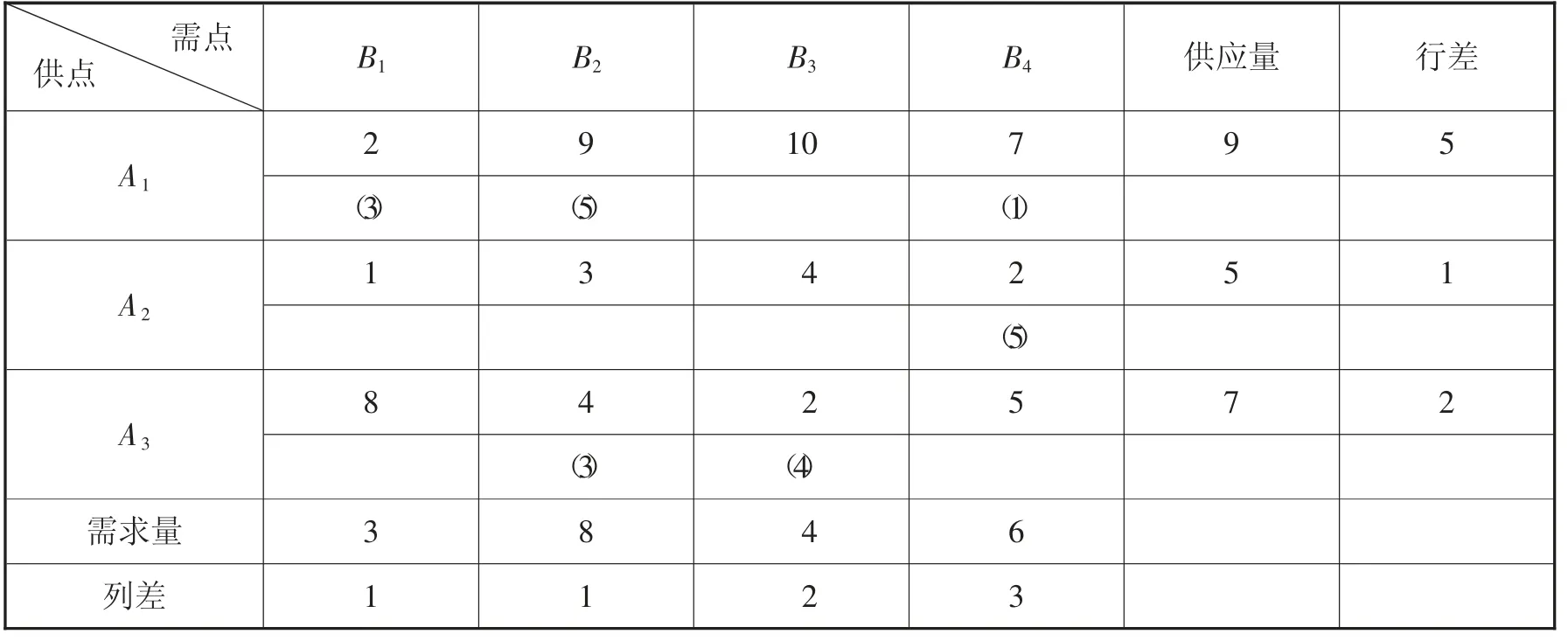
表3 初始调运方案
第二步:从行差额或列差额中选出最大者,再对所选择的最大行(列) 差,选择其所在行或列中的最小运价元素(如行差中最大为5,选最小元素为2),于是可确定A1供应点的航材运往需点B1,由于B1的需求为3,A1的供应能力为9,B1的需求得到满足,去掉B1的需求量这一列(若A1的供应能力小于B1的需求量,则去掉A1这一行),以示B1已不再参与航材的分配。对已划去的列(或行) 得到的新的供需平衡表用同样的方法进行分配,最后得到的数字为表3 中带括号的数字,即为初始调运方案。
(2) 检验初始调运方案是否为最优调运方案
表4 为得到的初始调运方案。
应用位势法判断该调运方案是否为最优方案。

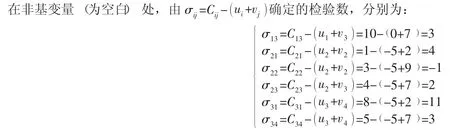

表4 初始调运方案
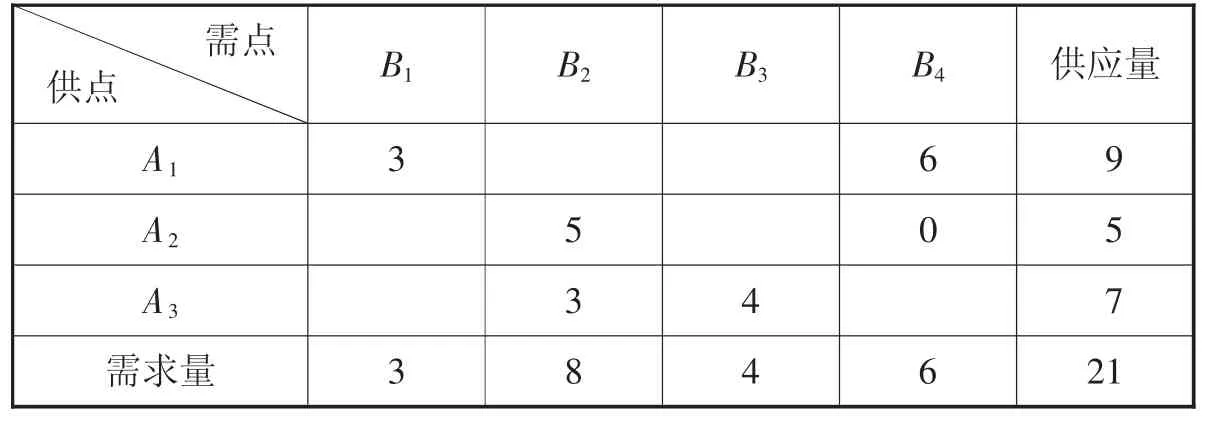
表5 调整方案
空白(非基变量) 检验数σ22为负数,所以上述初始调运方案不是最优方案,需进行调整。X22(=y)为换入变量,X22作为第一个顶点,以基变量中的点作为其他顶点构造闭回路为:X22,X12,X14,X24,其偶数顶点为X12,X24,调整量为min(X12,X24)=min(5,5 )=5,以X12(或X24) 为换出变量,在闭回路中奇数顶点加上调整量,偶数顶点减去调整量,得新的调运方案如表5 所示。
值得注意的是,在此X12已作为换出变量,调运量为0,不能填在调运方案表中,而X24虽然调运量为0,但X24是作为基变量出现在调运方案中的,必须填上(否则新基变量就少于m+n-1 个)。
对新得到的调运方案再进行检验、调整,直到所有的空白检验数为非负,对表5 的调运方案进行检验,由σij=Cij-(ui+vj)=0,再次确定新ui,vj的值:

根据新得的ui,vj,求出空白检验数:

同理有:
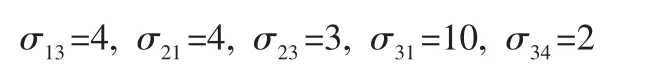
即所有空格检验数均为非负数,因此上述调运方案为最优方案,其最小目标值为:
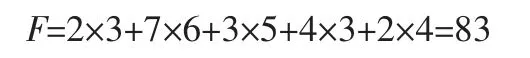
4 注意事项
在确定初始调运方案时,当确定Ai调给Bj时,如果存在ai=bj,则确定调运量为ai,同时划去Ai行与Bj列,并在Ai行(或Bji列) 任意一空格填上数字0,保证基变量的个数为m+n-1 个;如表中只剩下一个未划去的运价元素时,只填一个调运量,划去该行和该列。此时共划去m+n条线,填入m+n-1 个数,即给出m+n-1 个基变量。

