一种非中心点处声场重建方法

王 松 张 聪

(武汉轻工大学数学与计算机学院 湖北 武汉 430048)

0 引 言

随着首部3D电影的热播，3D影视技术受到大家的热捧，截至2017年，我国3D影院基本达到全覆盖。随着3D影音技术的飞速发展，3D音频技术已经成为多媒体领域的研究热点。当前三维音频技术包括Ambisonics[1-5]，波场合成(Wave Field Synthesis，WFS)[6-10]，头相关传输函数(Head Related Transfer Function，HRTF)[11-14]，矢量基幅废平移(Vector Based Amplitude Panning，VBAP)[15-16]等。其中，VBAP是一种重要的三维音频技术。

VBAP利用向量的观点，使用两个或三个扬声器合成一个虚拟声源，以达到声音定位的目的。在三维VBAP中，虚拟声源通过三个扬声器利用向量合成的原则合成虚拟声源[15-16]。VBAP具有计算效率和声像重建精度较高的优点。相较于Ambisonics，VBAP中的扬声器可以自由摆放，不必均匀摆放；相较于WFS，VBAP使用扬声器的数目较少，应用成本较低；相较于利用HRTF的三维定位方法，VBAP的计算效率较高。

2009年，Ando等[17]提出一种基于声压向量的三维平移方法，其核心思想是：虚拟声源在接收点处产生的声压向量与三个扬声器在接收点处产生的声压向量相等。该方法要求虚拟声源对应向量的方向位于三个扬声器构成球面三角形的内部。当三个扬声器和虚拟声源位于同一球面时，该方法得到的结果与VBAP的结果一样。

2011年，Ando[18]提出了一种基于声压和质点速度的三维平移方法。该方法使用三个扬声器合成一个虚拟声源，三个扬声器和虚拟声源位于同一个球面上，合成的原则是虚拟声源在接收点处产生的声压和质点速度的方向与三个扬声器在接收点处产生的声压和质点速度的方向相等，从而计算得到三个扬声器的分配系数。该方法为VBAP提供了物理基础。

2013年至2014年间，针对扬声器数目多于三个时扬声器需要分组的问题，文献[19-20]提出一次使用五个或者四个扬声器合成一个虚拟声源的方法，进一步推广了VBAP技术。

文献[15-20]都是以中心听音点为接收点，所有扬声器与虚拟声源都位于同一球面上，中心听音点处的三维声场重建效果最好。中心听音点被称为“甜点”或者“皇帝位”。其原理都是保证中心听音点处的声音物理性质不变，而忽略了非中心听音点处声音物理性质的保持，导致非中心听音点处声场重建效果较差。在实际应用场景中，听音者也可能处在或者运动到非中心听音点处，因此非中心听音点处三维声场的重建质量的保持具有现实意义。当前已有一些非中心听音点处或非中心区域的三维声场重建技术如同区域压力匹配技术[21](Pressure Matching in a Same Zone，PMSZ)和同区域质点速度匹配技术[22](Particle Velocity Matching in a Same Zone，PVMSZ)。PMSZ在原始系统与重建系统的同一区域内部匹配声压，PVMSZ在原始系统与重建系统的同一区域内部匹配质点速度。从理论上讲，它们均可用于非中心区域声场重建。但是已有一些实验结果表明，在非中心区域声场重建时，PMSZ与PVMSZ的重建误差较大，因此需要研究更好的非中心点或者非中心区域声场重建方法。

针对已有技术存在的问题，本文提出一种将非中心听音点中心化的方法，通过扬声器信号的二次分配在局部范围内使用三个扬声器合成一个虚拟声源，不断重复这一过程实现10个扬声器重建原始22声道系统，同时提高非中心听音点处重建三维声场的质量。本文主要贡献如下：(1)传统方法重建声场时如VBAP和文献[18]方法等，中心听音点处重建效果最好，但非中心听音点处重建效果较差。本文以非中心点为中心，构建虚拟扬声器阵列，通过虚拟扬声器阵列恢复非中心点处的声场。通过保证虚拟扬声器和实际扬声器在非中心点处产生的质点速度不变，将虚拟扬声器信号转换成实际扬声器信号，最终通过实际扬声器信号重建非中心点处的声场。(2)实现了利用10声道系统在非中心点处重建原始22声道系统的声场。实验结果表明，10声道系统重建精度较高。

1 声压与质点速度的概念

假设单个扬声器(单个扬声器可视作虚拟声源或者点声源)所在的位置为ξ=(ξx,ξy,ξz)T，接收点(也即听音点)所在位置为η=(x,y,z)T，则单个扬声器在接收点处产生的声压为：

(1)

式中：i为虚数单位；k=2πf/c为波数；f为声音信号的频率；c表示声音的传播速度；s(ω)为扬声器输入信号的傅里叶变换；G表示距离扬声器单位距离处的声压与扬声器信号之间的比例系数。

单个扬声器在接收点处产生的质点速度为：

(2)

2 文献[18]方法

如图1所示，假设一个虚拟声源和三个扬声器位于同一个球面上，虚拟声源位于三个扬声器构成球面三角形的内部，接收点位于中心点O(0,0,0)处。虚拟声源的坐标为vs(vsx,vsy,vsz)，三个扬声器的坐标为ξ1=(ξ1x,ξ1y,ξ1z)T，ξ2=(ξ2x,ξ2y,ξ2z)T，ξ3=(ξ3x,ξ3y,ξ3z)T，它们的极坐标表示分别为：(ρ0,θ0,φ0)、(ρ1,θ1,φ1)、(ρ2,θ2,φ2)、(ρ3,θ3,φ3)。

图1 扬声器摆放、虚拟声源位置图

虚拟声源在接收点处产生的质点速度为：

(3)

式中：λ表示空气密度。虚拟声源在接收点处产生的声压为：

(4)

三个扬声器在接收点处产生的质点速度为：

(5)

式中：

W=(w1,w2,w3)T为三个扬声器的信号分配系数。三个扬声器在接收点处产生的声压为：

(6)

由下式：

(7)

通过近似求解可以得到三个扬声器的分配系数[21]为：

(8)

式中：

D=D1+D2+D3

D1=sin(θ3-θ2)cosφ3cosφ2sinφ0+[sin(θ0-θ3)·

cosφ3sinφ2-sin(θ0-θ2)cosφ2sinφ3]cosφ0

D2=sin(θ1-θ3)cosφ1cosφ3sinφ0+[sin(θ0-θ1)·

cosφ1sinφ3-sin(θ0-θ3)cosφ3sinφ1]cosφ0

D3=sin(θ2-θ1)cosφ2cosφ1sinφ0+[sin(θ0-θ2)·

cosφ2sinφ1-sin(θ0-θ1)cosφ1sinφ2]cosφ0

3 方法设计

本文提出方法的整体流程如图2所示。

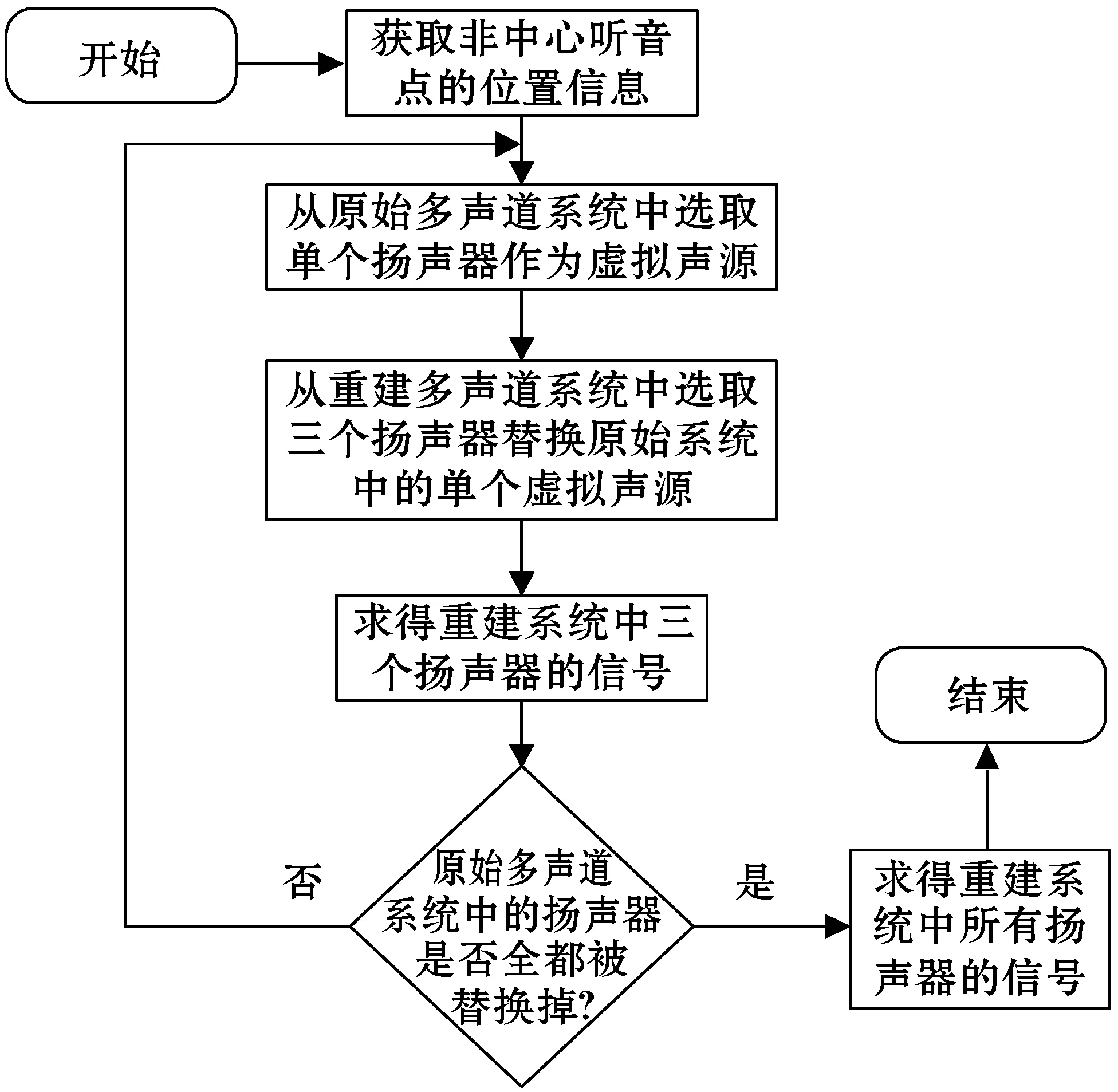
图2 提出方法整体流程图

图3 实际扬声器、虚拟扬声器摆放以及虚拟声源位置图

(9)

(10)

当以点O′为中心时，v1、v2、v3的极坐标分别为(ρv1,θv1,φv1)、(ρv2,θv2,φv2)、(ρv3,θv3,φv3)，它们的计算公式为：

(11)

式中：

当以为O中心点时，O′为非中心点，此时点v1、v2、v3的直角坐标分别为：

(13)

然后利用v1、v2、v3处虚拟扬声器信号求解ξ1、ξ2、ξ3处实际扬声器信号。当O为坐标原点时，点vj(j=1,2,3)处虚拟扬声器在点O′处产生的质子速度为：

(14)

vj处虚拟扬声器对应的ξj处实际扬声器在点O′处产生的质子速度为：

(15)

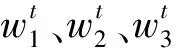
(16)

可以得到：

(17)

式中：I为单位矩阵；λ为规则化因子。

不断重复上述过程，将原始声场中的每个虚拟声源使用重建系统的三个扬声器逐渐全部替换掉，每次求得三个扬声器的分配系数，它们乘以被替换虚拟声源的信号即可求出三个扬声器的信号，最后将重建系统中扬声器的信号进行叠加，得到最终重建系统中扬声器的信号。

4 仿真实验

4.1 实验结果

本文通过计算机模拟实验比较本文方法和Ando、PMSZ、PVMSZ传统方法在非中心点处三维声场重建的效果。本文使用10声道系统重建NHK22.2多声道系统，两个低音效果声道不作处理。原始系统与重建系统的扬声器摆放位置结构图参见图4，这些扬声器摆放位置都是NHK研究人员设计出来用于听音测试的。原始系统与重建系统的扬声器分别位于以坐标原点O(0,0,0)为中心，2 m为半径的球面上，非中心点所在位置为O′(0.5,0.5,0)(直角坐标表示)，黑色实心点表示扬声器所在的位置。声音速度为340 m/s，人头半径为0.085 m。仿真实验采用原始声源的信号为900 Hz进行实验。

(a)原始22声道系统

当虚拟声源信号频率f=900 Hz时，原始22声道系统产生声场与重建10声道系统产生声场的对比图如图5所示。可以看出，相较于传统方法，本文提出方法在非中心点O′周围产生的声场更加接近于原始系统声源在非中心点处产生的声场。

(a)原始系统产生的声场图

相对均方误差(Relative Mean Square Error，RMSE)被用来衡量重建声场相对于原始声场的误差大小。它的定义表达式为：

(18)

式中：S表示以O′为球心的球体；球体半径为r；Po表示原始声源在球体S内部产生的声压；Pr表示重建系统中声源在球体S内部产生的声压。传统方法和提出方法产生的相对均方误差对比参见图6。

图6 相对均方误差对比图

可以看出，在以非中心点O′为球心的球体内部，当球体半径逐渐增大时，本文方法的相对均方误差整体上是逐渐增大的。在球体半径r的所有可能的取值范围内，本文方法产生的相对均方误差比文献[18]和文献[21]方法产生的相对均方误差都低；当球体半径r取值范围是[0.085,0.51]m和[1.105,1.275]m时，本文方法产生的相对均方误差比文献[22]方法低；当球体半径r取值范围是[0.595,1.020]m时，本文方法产生的相对均方误差比文献[22]方法略高，但是不超过5%。特别地，当球面半径r=0.085 m即人头半径大小时，如表1所示。本文方法产生的相对均方误差为1.27%(<4%，可以满足实际应用需求[23])，比文献[18]、文献[21]和文献[22]方法分别低30.64、60和30.55个百分点。这表明在单个人头半径内，即一个听音者进行听音时，本文方法显著优于所有传统方法。当球体半径大于0.51 m时(即大于6个人头半径大小)，本文方法产生的相对均方误差仍然低于文献[18]和文献[21]方法，但是与文献[22]方法相差不大。

表1 当r=0.085 m时，相对均方误差比较 %

时间平均声音强度的定义为：

(19)

式中：“*”表示复共轭；“Re”表示复数的虚部。时间平均声音强度可用于分析声音强度流，它表示一段时间之内的平均瞬时强度。强度流表示时间平均声音强度的方向，其数学表达式为：

(20)

强度流误差的定义为：

(21)

式中：IFod(O′,ω)表示原始声场的强度流；IFrd(O′,ω)表示重建声场的强度流。

不同方法的强度流误差比较如图7所示。黑色圆圈的半径为0.085 m，表示以人头半径为半径的区域。可以看出在黑色圆圈范围内，文献[21]方法产生的强度流误差低于文献[18]方法和文献[22]方法，而本文方法产生的强度流误差低于所有传统方法。

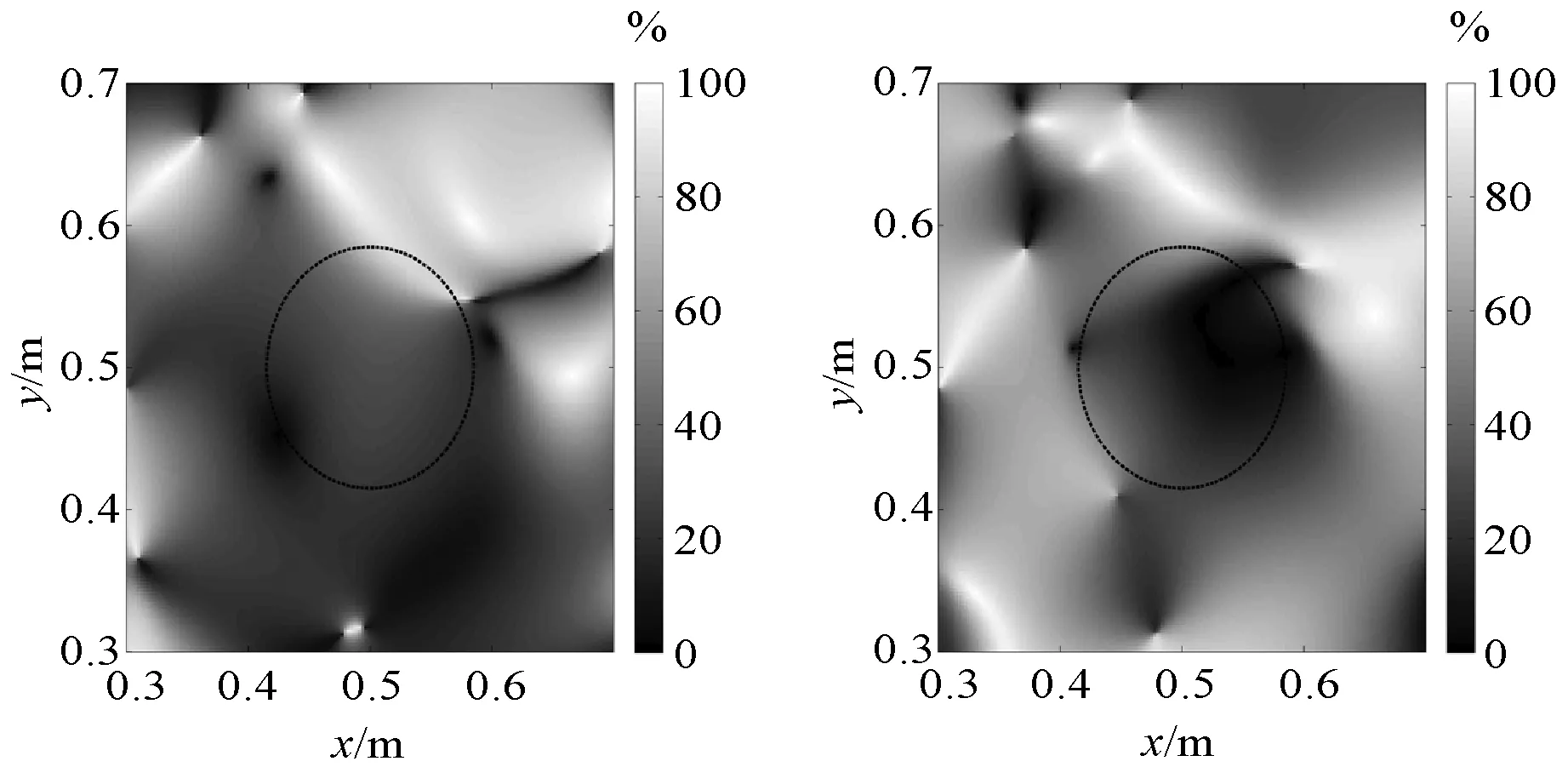
(a)文献[18]方法 (b)文献[21]方法

在以O′(0.5,0.5,0)为中心点，人头半径0.085 m为半径的非中心区域内部，当声音信号频率变化范围为[50,900]Hz时，不同方法产生的相对均方误差如图8所示。

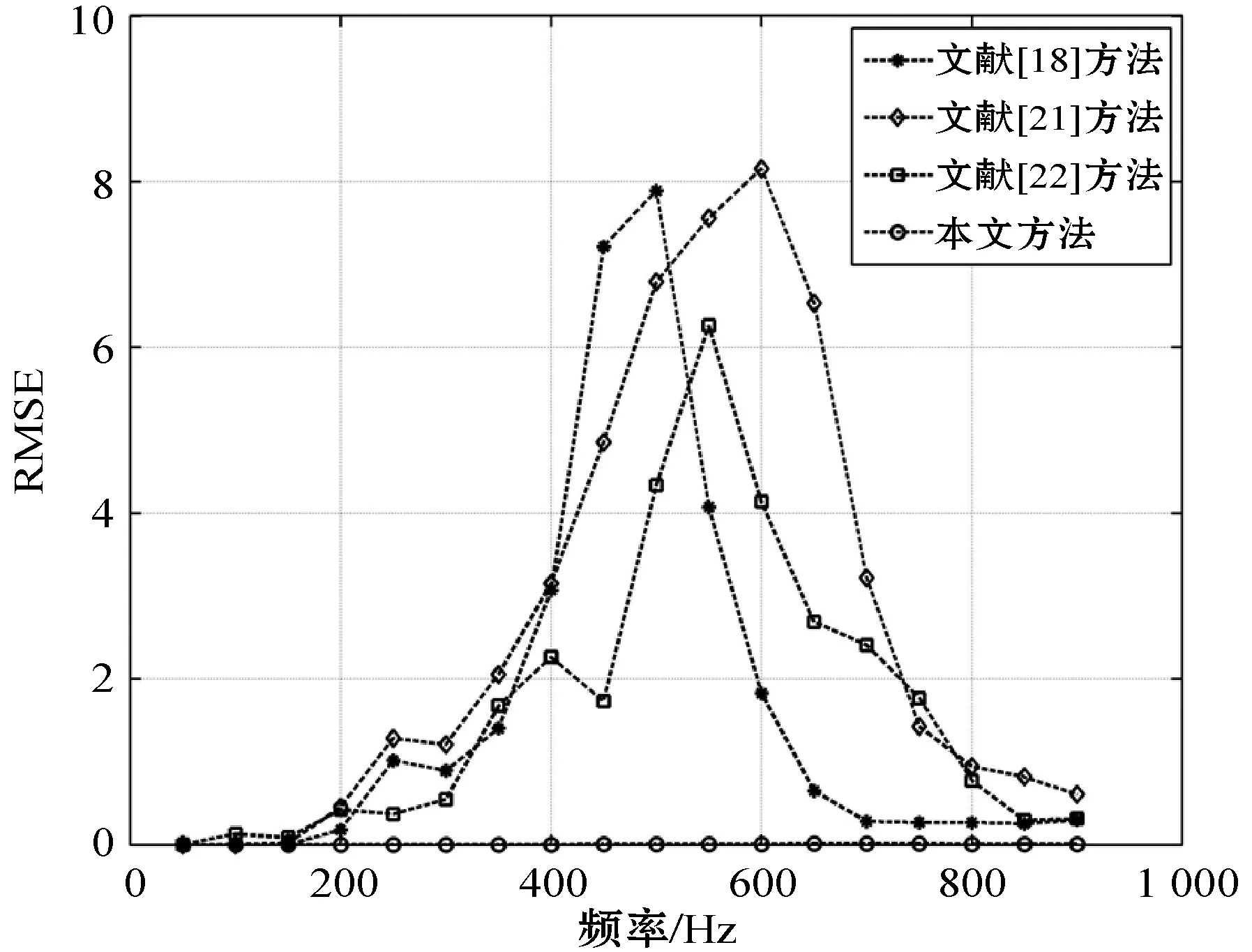
图8 相对均方误差与信号频率之间的关系对比图

可以看出，随着信号频率的变化，本文方法产生的相对均方误差最低，其变化范围是[0,1.77%]；而文献[18]方法产生的相对均方误差变化范围是[0,789.28%]，文献[21]方法产生的相对均方误差变化范围是[0,815.92%]，文献[22]方法产生的相对均方误差变化范围是[0.67%,626.73%]。该实验表明当信号频率从50 Hz变化到900 Hz时，本文方法在单个人头区域范围内重建声场的质量比传统方法稳定。

平均相对均方误差(RMSE)是指所有与中心点(也即坐标原点)之间距离相等的非中心区域声场产生的相对均方误差的平均值，不同方法产生的平均相对均方误差的对比图参见图9。其中原始信号频率为900 Hz，非中心区域与中心点之间的距离变化范围是[0.085,0.935]m，非中心区域声场的半径为0.085 m。可以看出，随着非中心区域与中心点之间距离的逐渐变化，文献[18]方法产生的平均相对均方误差变化范围是[0.45%,288.17%],文献[21]方法产生的平均相对均方误差变化范围是[2.00%,299.14%],文献[22]方法产生的平均相对均方误差变化范围是[12.38%,220.16%],然而本文方法产生的平均相对均方误差变化范围是[0.17%,43.36%]，低于传统方法产生的平均相对均方误差。实验表明，当非中心区域所在位置发生变化时，本文方法重建声场的平均质量优于传统方法。

图9 平均相对均方误差与非中心区域和中心点之间距离的关系对比图

4.2 实验分析

上述非中心听音点处实验表明，本文方法优于传统的三种对比方法。其原因是：文献[18]方法只是关注中心听音点处声场得到最优恢复，不关注非中心听音点处声场的恢复情况，因此在非中心点处重建效果不好；文献[21]方法重建目标声场需要扬声器阵列均匀摆放[25]。然而当进行非中心点声场重建时，文献[21]方法中扬声器阵列相对于非中心点的摆放位置是不均的，因此在非中心点处的重建效果不佳；文献[22]方法虽然克服了扬声器阵列需要均匀摆放的问题，但是它在进行指定区域声场重建时，需要在使用同等数量扬声器的条件下同时恢复多个点处的声音物理性质，导致重建效果不如本文方法。

传统VBAP或者文献[18]方法的核心思想是当虚拟声源与扬声器位于同一个球面时，球体中心点处(也即中心听音点)的声场可以得到最佳恢复。本文的方法聚焦于非中心听音点处的声场恢复，借鉴传统方法的思想，以非中心点O′作为中心，以虚拟声源和非中心点之间距离作为半径构建虚拟球面。然后将实际扬声器映射到虚拟球面上得到虚拟扬声器的位置，此时虚拟声源和虚拟扬声器位于同一个虚拟球面上，非中心点O′变成了虚拟声源和虚拟扬声器的中心点。依据文献[18]方法的原理，O′处的声场可以得到最佳恢复，并可以由虚拟声源的信号求得虚拟扬声器的信号。再通过保证实际扬声器和虚拟扬声器在O′处产生的质子速度相等，由虚拟扬声器的信号求得实际扬声器的信号。通过这种声音信号的两次等价转换可以保证非中心点O′处的声场得到较为准确的恢复，所以重建效果优于传统方法。

5 结 语

针对目前已有三维声场重建方法存在非中心点处声场重建误差较大的问题，本文提出了一种非中心点处声场重建方法。借鉴了传统方法中中心点处声场最优恢复的思想，通过构建虚拟扬声器阵列和虚拟扬声器的信号与实际扬声器信号之间的转化，实现非中心点处声场重建，拓宽了已有方法的适用场景和使用范围。仿真实验结果表明：在单个人头区域内，本文方法在非中心点周围的声场重建、相对均方误差、强度流误差、平均相对均方误差这些比较指标上均优于传统方法。本文方法适用于单个听音者在非中心点处进行听音，证实了其有效性。