圆的综合题考法浅析

湖北省咸丰县坪坝营镇杨洞中小学校 445605

如果说函数的综合运用是初中数学所学内容的全部的话，那么圆的综合题就是初中所学几何知识的全部。细读近十年恩施州中考数学试题，除2011年出现在21题外，近九年的23题都是圆的综合题，可以说具有绝对的稳定性，试题覆盖了初中所学几何的全部章节内容。

试题有两至三问，但第一问年年都是切线的证明，具有绝对的稳定性，第二、三问有求阴影部分面积的、角的度数的、证明线段相等的和求线段长度的，但求线段长度的居多。涉及到主要的知识点是：切线的性质和判定、三角形全等、等边（腰）三角形的性质、图形的面积、直角三角形两锐角的关系、线段垂直平分线的性质、圆周角定理及其推论、三角函数、勾股定理、垂径定理、相似三角形性质、特殊的四边形、平行线的性质和判定等，基本上覆盖初中阶段所学几何知识的全部。下面浅谈一下切线的证明方法和线段长度的求法。

一、切线的证明方法

近十年考题的切线证明都是根据切线的判定定理来证明的，及过半径的外端，且垂直于这条直径的直线就是圆的切线，解决问题的途径只有两种。

途径一：证明这条直线与半径所成的角与另一直角相等，来证明这条直线是圆的切线。如：21.（2011·恩施 本小题满分8分）如图，已知AB为⊙的直径，BD为⊙的切线，过B点的弦BC ⊥OD交⊙O于C点，垂足为M.

（1）求证：BD是⊙O的切线；

（2）当BC=BD，且BD=6cm时，求图中阴影部分的面积（结果不取近似值）.

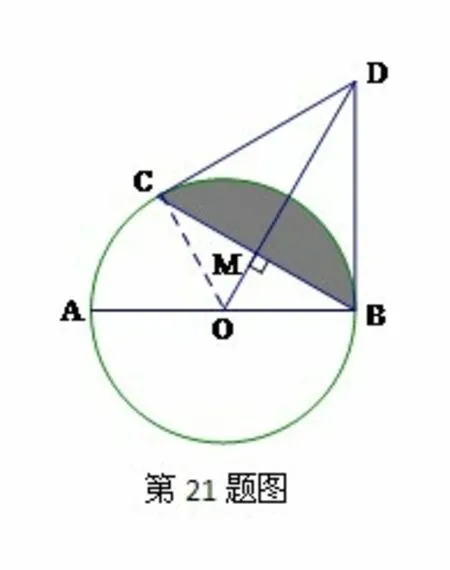
解决此题，可通过证明这条直线与半径所成的角与图中的直角相等，来得到这条直线是圆的切线。2013年中考的23题第一问也可用此方法来解决。23.（2013·恩施 满分10分）如图11，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD垂直AB于D点，交AE于F点，过C作AE平行线交BA的延长线于G点.

(1)求证：GC是⊙O的切线.

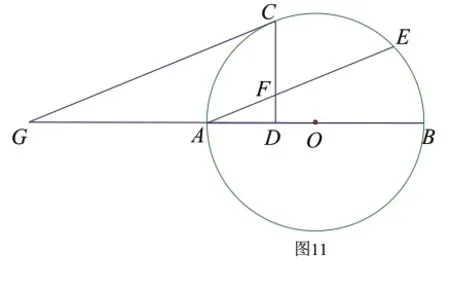
(2)求证：AF=CF

(3)若∠EAB=30O，CF=2求GA的长.

途径二：通过推理计算得出这条直线与半径所成的角是直角，来证明这条直线是圆的切线。如：23.（2014·恩施州）如图13，AB是⊙O的直径，CD是弦，AB ⊥CD，垂足为E，连接AC、AD，延长AB交过点C的直线于点P，且∠DCP=∠DAC

（1）求证：PC是⊙O的切线

（2）若AC ＝5，CD ＝6，求PC的长

此题就是直接计算这条直线与半径所成的角是直角，从而得到PC是⊙O的切线。

二、线段长度的求法

此类题求线段的长度常综合运用到等腰三角形的性质、垂径定理、勾股定理、三角函数、相似三角形性质、特殊的四边形的性质来解决。下面以2014·恩施州中考数学试题23题来说明（题图见前）

此题就运用了垂径定理、勾股定理、三角函数（相似△的性质）来解决。2013年中考题的23题第三问也可用类似的方法来解决。