随机和区间变量共存的结构可靠性分析算法

邱 涛，王增臣，游令非

(1.中国电子科技集团公司 第二十八研究所，江苏 南京 210000；2.北京航空航天大学 可靠性与系统工程学院，北京 100191；3.北京航空航天大学 可靠性与环境工程技术国防科技重点实验室，北京 100191)

0 引言

在机械结构(航空、航天、武器)服役过程中，工作环境愈加恶劣，不确定影响因素日趋增加，建立显式的结构可靠性模型比较困难。对于复杂机械结构，认知局限和客观随机性的存在使其在研制过程中充满不确定性[1]。当可靠性模型的输入变量信息较少时，很难得到输入变量的精确概率分布，可以采用分布未知、边界可知的区间变量进行描述[2-3]。

对于概率不确定模型，有一次二阶矩法(First Order Second Moment, FORM)[4-5]、HLRF(Hasofer-Lind and Rackwitz-Fiessler)[6-7]和aHLRF[8]。对于区间不确定模型，唐忠等[9]基于偏弹性理论，构造了一种含区间变量的二阶多项式功能函数；Wang等[10]考虑不确定信息对系统结构安全的影响，提出一种基于非概率集合理论的区间可靠性分析方法；孙静怡等[11]为抑制区间算法导致的区间扩张问题，提出一种区间仿射响应面法。

对于概率—区间混合的可靠性模型，Elishakoff等[12]基于凸模型理论，提出一种解决混合可靠性问题的分析方法；Luo等[13]提出一种迭代算法，用于寻找不确定性空间中的最坏情况点和最可能故障点，以计算可靠性指标；Qiu等[14]将区间方法引入传统可靠性理论，获得系统失效概率区间；Du[15-16]针对概率—区间混合的可靠性问题，提出一种概率分析与区间优化嵌套处理的双层优化模型，但在工程实际中功能函数大多为隐式，采用该方法会大大降低计算效率；姜潮等[17-18]基于Bucher建立线性响应面，提高了混合可靠性分析的计算效率；Alibrandi等[19]基于一次二阶矩法，通过较好地近似设计点来提高计算效率，但对于非线性程度较高的功能函数，计算精度会降低；Xie等[20]在考虑区间变量相关的情况下，用单步可靠性序列迭代算法求解双层优化模型；Gao等[21]提出一种统一区间随机可靠性抽样方法，用于评估涉及多个不精确随机场的工程结构的安全性。根据以上研究表明，当功能函数为隐式表达式时，存在计算效率降低的问题；当功能函数非线性程度较高时，会导致计算结果不收敛或使计算精度下降。

针对以上问题，基于响应面法和一次二阶矩法，本文提出一种高效的混合可靠性分析算法。当功能函数为隐式表达式时，为减少原始极限状态函数的调用次数，提出一种基于二次插值抽样的响应面法；当功能函数非线性程度较高时，针对计算结果不收敛或计算精度下降的问题，提出一种基于二参数寻优设计点的概率分析算法。

1 概率—区间混合可靠性模型

结构的可靠性受材料属性、几何尺寸、环境载荷等多种不确定因素影响，其功能函数可表示为

g(Z)=g(X,Y)。

(1)

式中Z=(X,Y)，X=[X1,X2,…,Xn]T表示随机变量，Y=[Y1,Y2,…,Ym]T表示区间变量。当g(Z)>0时，结构安全；当g(Z)<0时，结构发生失效；当g(Z)=0时，结构处于极限状态。

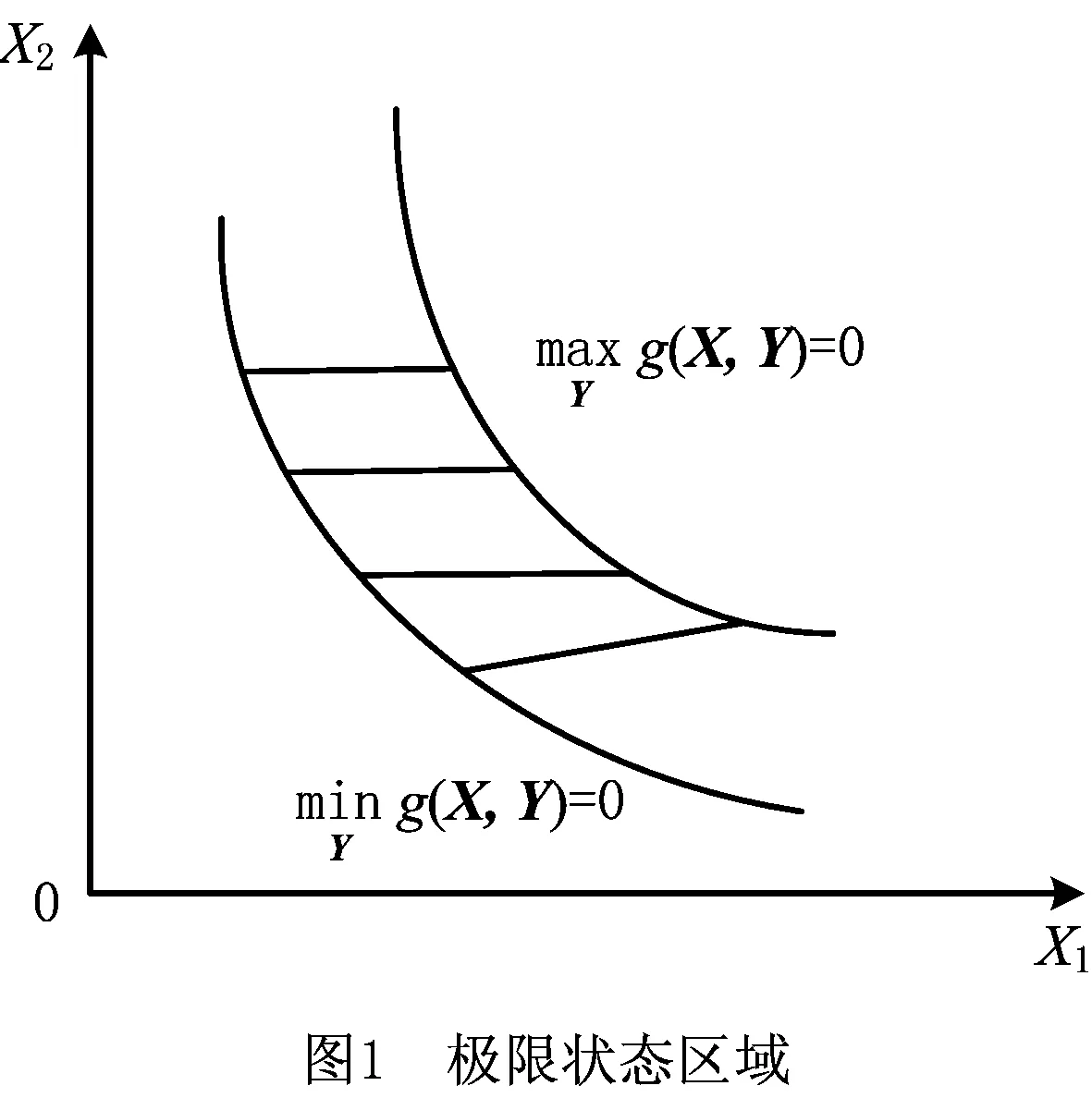
根据图1可知，失效概率Pf为一区间范围，可表示为[15]：

(2)

(3)

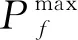
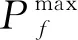
2 基于二次插值抽样的响应面法

由于功能函数含有区间变量，不能直接进行可靠度求解，首先采用高维模型表示(High Dimensional Model Representation, HDMR)模型将混合可靠性模型解耦为单层可靠性模型。在拟合单层可靠性模型时，为减少原始极限状态函数的调用次数，提出二次插值抽样法(Quadratic Interpolation Sampling, QIS)进行抽样。

2.1 单层可靠性模型

HDMR是一种近似函数模型，低阶的HDMR模型同样具有较高的拟合精度[22]。

基于高维模型表示方法，g(Z)可表示为

(4)

式中：l=n+m；g0为0阶分量函数；gr(Zr)为1阶分量函数；grs(Zr,Zs)为2阶分量函数；grst(Zr,Zs,Zt)为3阶分量函数；g12…l(Z1,Z2,…,Zl)为所有残余的耦合输入变量对响应值的影响。

因为HDMR展式中的1阶分量函数gr(Zr)是泰勒展式中仅含变量Zr的集合，所以1阶分量函数gr(Zr)可以为非线性。通过引入HDMR展式的1阶分量函数，将功能函数解耦为随机和区间变量相互分离的单元函数，近似表达为

(5)

式中：c为拟合近似表达式的参考点；g(Xi)为仅包含随机变量Xi的单元函数；g(Yj)为仅包含区间变量Yj的单元函数。

2.2 二次插值抽样法

在抽取样本点时，提出了QIS，第1次插值用于确定参考点，使参考点更加靠近功能函数；第2次插值用于确定拟合样本点，降低抽样系数对样本点位置的影响。

(6)

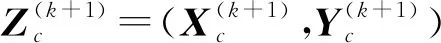
s=1,2,…,l；

(7)

s=l+1,l+2,…,2l。

(8)

虽然CS能在参考点附近很好地拟合响应面，但是抽取的样本点与抽样系数f的关系较大，导致计算结果对f较为敏感。如果f过大，则样本点距功能函数较远，导致拟合精度下降；如果f过小，则样本点较为密集，导致拟合矩阵奇异。

(9)

(10)

r=l+1,l+2,…,2l。

(11)

3 可靠性分析

因混合可靠性模型被解耦为随机和区间变量分离的单层可靠性计算模型，可对含随机变量的单元函数进行概率分析，对含区间变量的单元函数进行区间分析。

3.1 基于二参数寻优设计点的概率分析

在概率分析时，基于FORM，通过增加两个参数η和λ来调整每一次迭代的搜索步长和搜索方向，提出基于二参数寻优设计点的一次二阶矩法tHLRF。

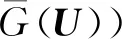
(Uk+1-Uk)。

(12)

式中:Uk为第k次迭代的设计验算点(Most Probabile Point, MPP)；Uk+1为第k+1次迭代的MPP；G(Uk)为功能函数G(U)在Uk处的梯度；为功能函数G(U)在Uk处的一阶泰勒展开。

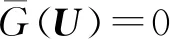
(13)

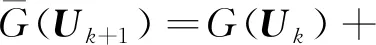
=ηG(Uk)。

(14)

式中η∈[0,1)。

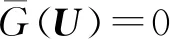
考虑取步长λ为有限值，以改变寻优设计点的搜索方向，可得辅助点Hk+1，

(15)

式中λ为从Uk沿-G(Uk)方向移动的步长。

在平面G=ηG(Uk)上，Uk+1的搜索方向为原点到辅助点Hk+1的方向，其方向余弦矢量

(16)

Uk+1=βk+1αk+1。

(17)

式中βk+1为第k+1次迭代的可靠度指标。

将式(17)代入式(14)，求解得可靠度指标

(18)

根据求得的可靠度指标βk+1，由式(17)得第k+1次迭代的MPP的Uk+1。

在选择参数η时，初始值设定为较小的值，可取η=0.1，在迭代过程中，设定ηk+1=0.1+ζηk以自适应更新参数η，ζ为η的调整系数，一般取在0.01～0.05之间；在选择参数λ时，初始值设定为较大的值，可取λ=50，在迭代过程中，设定λk+1=λk/ξ以自适应更新参数λ，ξ为λ的参数调整系数，一般取在1.2～1.5之间。

3.2 区间分析

在第k+1次迭代中，含区间变量的单元函数为g(Y)，区间分析可表示为式(19)的区间优化问题：

s.t.

YL≤Y≤YR。

(19)

式中：Yk+1为第k+1次迭代的区间最优点；YL为区间的下界矢量；YR为区间的上界矢量。

通过KKT条件判断当前迭代点是否为最优点：

(20)

(21)

式中：j=1,2,…,m表示m维区间变量的第j维；Yk为第k次迭代的区间最优点。

若满足KKT条件，则Yk+1=Yk；若不满足，则进行区间优化分析[23]。设当前为第r次迭代，迭代点为Yr，将此区间优化问题转化为二次规划问题：

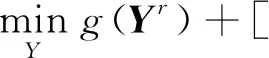
s.t.

YL≤Y≤YR

。

(22)

式中Hs为Hessian矩阵。

式(22)为区间约束的二次规划问题，采用梯度投影法[24]可将迭代方向投影到区间可行域上，以高效计算含区间变量单元函数的最优点。若新迭代点Yr+1满足KKT条件，则区间迭代停止，Yk+1=Yr+1。

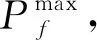
(23)

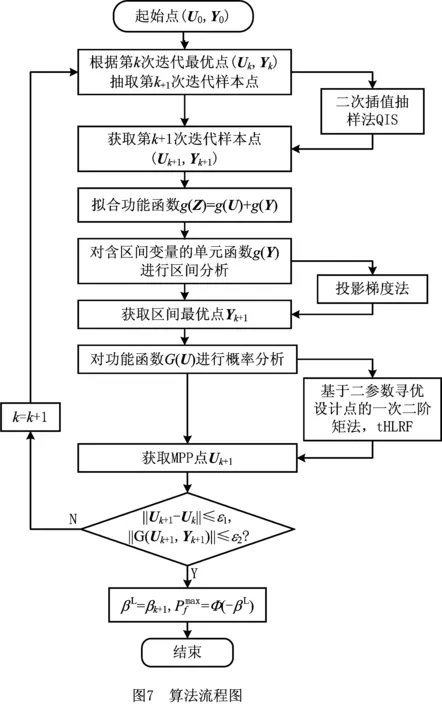
综上所述，论文所提可靠性分析算法的流程图如图7所示。

4 案例分析

在两个案例分析中，收敛精度ε1=ε2=1×10-6，在概率分析时，初始参数η=0.1，λ=30，参数调整系数ζ=0.05,ξ=1.2；N为可靠性分析算法的迭代循环次数，t为算法计算所耗时间。

4.1 悬臂梁案例

如图8和图9所示，悬臂梁长度为L，横截面高度为h，宽度为w，材料的弹性模量为220 GPa，在其末端作用的水平和垂直载荷分别为Px，Py。悬臂梁末端的许用位移不超过δ=56 mm，考虑Px和Py为区间变量，L，w，h服从正态分布，其不确定特征参数如表1所示。

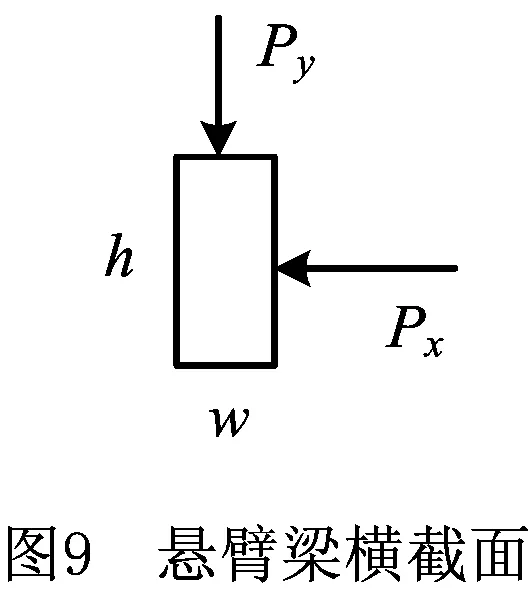
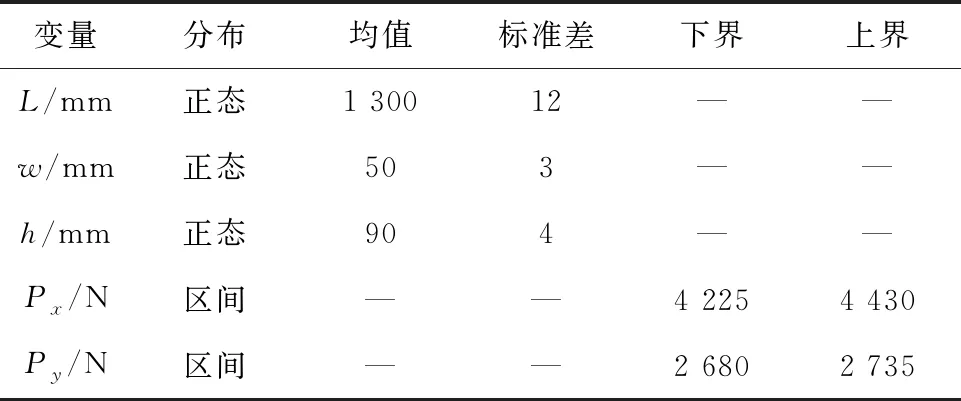
表1 悬臂梁的不确定特征

因为悬臂梁末端的许用位移不超过δ=56 mm，所以功能函数表示为

为验证所提算法的精度，将每个区间等分为10份，采用蒙特卡洛采样法(Monte Carlo Sampling，MCS)在区间变量的组合值下对随机变量抽取1×108次，调用功能函数1×1010次。根据表2可知，相比MCS，所提算法的相对误差为4.2%，验证了该算法的精度。

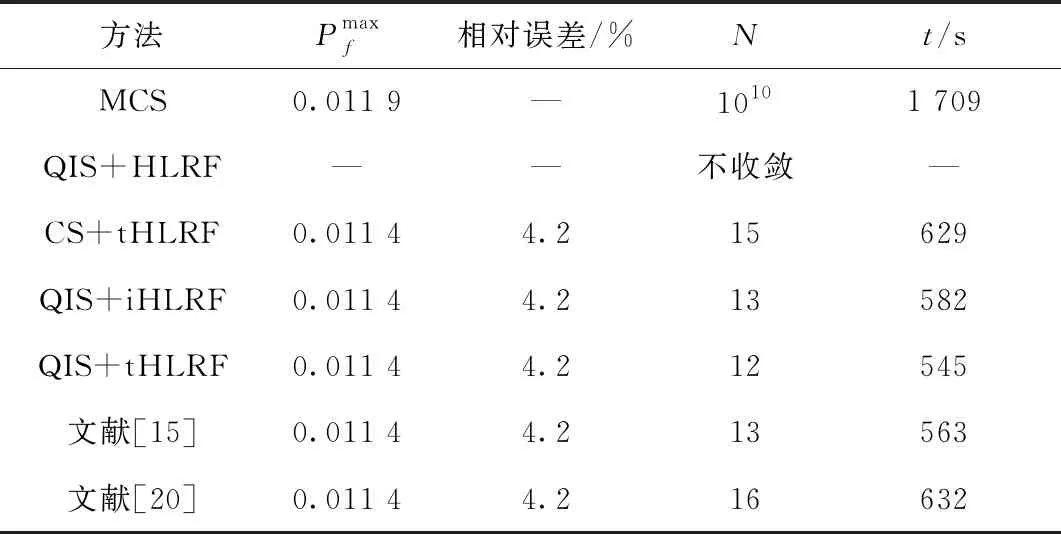
表2 悬臂梁最坏情况下的失效概率

根据图10不同可靠性分析算法收敛过程的对比和表2可知，基于CS+tHLRF的混合可靠性分析算法在迭代循环15次后达到收敛，可靠度计算时间为629 s；基于QIS+tHLRF的混合可靠性分析算法在迭代循环12次后达到收敛，可靠度计算时间为545 s。相比经典抽样法，验证了论文所提QIS具有更高的效率。

基于QIS+FORM分析算法的可靠度计算结果不收敛；基于QIS+iHLRF[25]分析算法迭代13次后收敛，可靠度计算时间为582 s。对比基于FORM的混合可靠性分析算法，当功能函数的非线性程度较高时，所提基于tHLRF的混合可靠性分析算法同样满足收敛要求，相比基于iHLRF的混合可靠性分析算法，验证了所提基于tHLRF的混合可靠性分析算法具有更高的计算效率。文献[15]为该类方法典型的研究成果，主要用于解决功能函数为显示表达式的问题，可靠度计算时间为563 s；文献[20]为该类方法中较新的研究成果，可靠度计算时间为632 s。相比文献[15,20]，同样验证了本文所提算法具有较高的计算效率。

根据以上对比结果可知，在同样收敛精度要求下，QIS较经典抽样法具有更高的计算效率；当功能函数非线性程度较高时，tHLRF能解决收敛不稳定的问题，而且具有较高的计算效率。与该领域中的研究成果对比，说明本文所提算法在保证计算精度的条件下具有较高的计算效率。

4.2 工程案例

表3 压气机轮盘的不确定特性

案例的工况条件为低循环疲劳试验，其转速为9 550 r/min，30 s为一个周期，温度为230℃恒温。轮盘经过105 300次试验循环，耗时约877 h，在销钉孔处产生初始裂纹[26]，裂纹如图11所示。

由于压气机轮盘沿圆周均匀对称分布37个销钉孔，现选取轮盘的1/37作为计算模型(其有限元模型如图12)，并对轮盘销钉孔周围的网格进行了加密。

通过上述模型对轮盘进行有限元分析，应变分析结果如图13所示，同样得出压气机轮盘的关键部位为销钉孔。现对该轮盘建立疲劳可靠性模型，计算该压气机轮盘在寿命为8 000周下的失效概率。

根据Coffin-Manson公式，结合Miner法则[27]建立轮盘的低循环疲劳可靠性模型。

裂纹形成寿命NS采用Coffin-Manson公式求解：

(24)

由Miner法则，若构件在应力载荷水平Sj作用下经受nj次循环的损伤为Tj=nj/Nj，则当构件承受k个载荷水平作用时，所受累计损伤

(25)

结构危险点的功能函数

g(Z)=g(X,Y)=a-T(Z)。

(26)

式中：Z=(X,Y)，X=[X1,X2,…,Xn]T为影响疲劳寿命的随机变量，Y=[Y1,Y2,…,Ym]T为影响疲劳寿命的区间变量；a为损伤强度，a=1。

根据以上疲劳可靠性模型，采用不同可靠性分析算法求解轮盘的最大失效概率，收敛过程与计算结果分别如图14和表4所示。

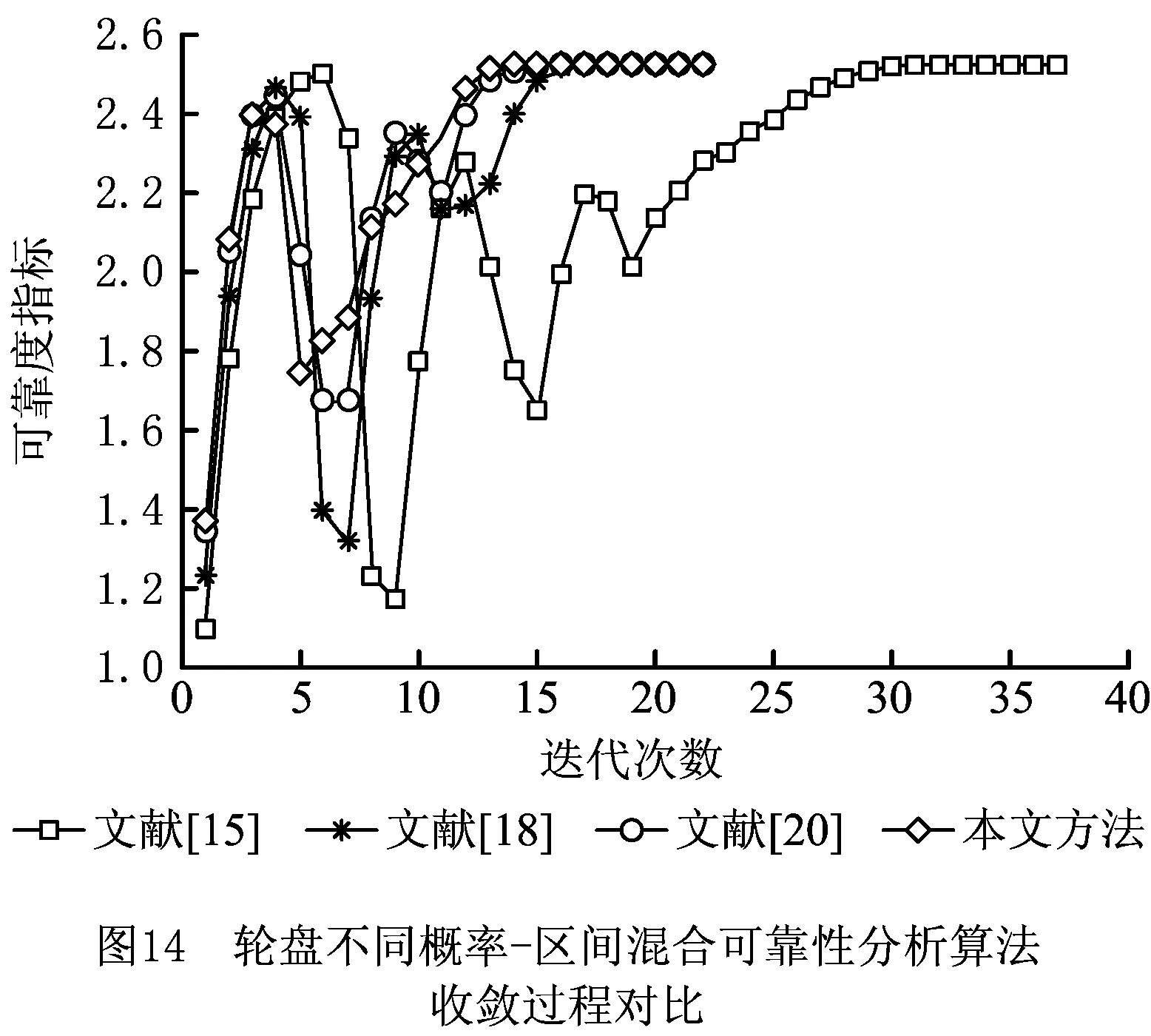
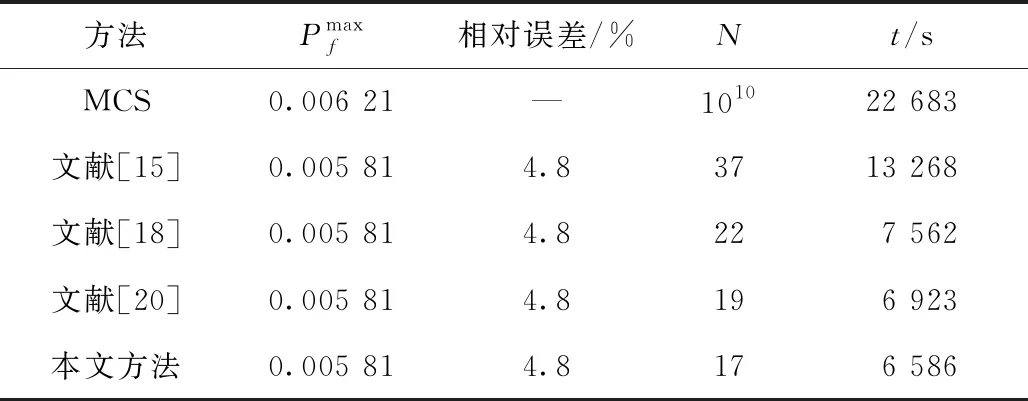
表4 轮盘最坏情况下的失效概率

在该工程对象中，无法得到压气机轮盘的显式功能函数，首先根据轮盘失效机理建立疲劳可靠性模型；其次采用基于二次插值抽样的响应面法拟合功能函数；最后利用所提可靠性分析算法求解失效概率。根据表4可知，相比MCS，所提算法计算结果的相对误差为4.8%，既验证了所提算法的精度，又说明其可以解决工程中难以建立显式功能函数的结构可靠性问题。

由图14和表4可知MCS计算用时22 683 s，文献[15]主要针对功能函数为显式表达式的可靠度计算方法，其迭代37次收敛，可靠度计算用时13 268 s；文献[18]为同类方法中功能函数为隐式表达式时的典型研究成果，其迭代22次收敛，可靠度计算用时7 562 s；文献[20]为同类方法中较新的研究成果，其迭代19次收敛，可靠度计算用时6 923 s；本文所提算法迭代17次收敛，可靠度计算用时6 586 s。通过与文献[15]对比，验证了结构的功能函数为隐式表达式时，所提算法可以减少原始极限状态函数的调用次数；通过与文献[18,20]对比，验证了所提算法具有较高的计算效率。在大型工程实例中，功能函数多为隐式表达式，计算耗时较长，而采用所提算法具有较高的计算效率，说明所提算法具有较好的工程应用价值。

5 结束语

针对概率—区间混合的可靠性问题，本文提出一种高效的可靠性分析算法，为解决混合结构可靠性问题提供了新的参考。具体贡献如下：

(1)提出QIS，使样本点尽可能落在真实功能函数附近，降低了插值系数f对样本点位置的影响，减少了对原始极限状态函数的调用次数，提高了计算效率。

(2)提出基于二参数寻优设计点的概率分析算法，在寻优MPP时，引入两个调整参数和两个自适应参数调整系数，分别控制搜索方向与搜索步长，解决了功能函数非线性程度较高时计算结果收敛不稳定的问题，并提高了计算效率。

(3)本文提出的结构可靠性分析算法适用于通用的随机和区间变量共存的结构可靠性问题，对实际工程应用具有一定的指导意义。

本文引入的两个自适应调整系数为在一定的范围内取值，后续研究将考虑采用优化函数的形式，通过求解自适应调整系数来提高可靠度的计算效率。