一种多假设联合相容SLAM数据的关联方法

徐伊岑，曹小兵，郭剑辉

（1.无锡商业职业技术学院机电技术学院，江苏无锡 214153；2.无锡职业技术学院控制技术学院，江苏无锡 214121；3.南京理工大学计算机科学与工程学院，南京 210094）

0 引言

同时定位与地图创建（Simultaneous Localization and Mapping，SLAM）也称CML（Concurrent Mapping and Localization）问题，是移动机器人实现自主导航的关键问题之一［1-5］，其目的是使机器人在缺乏先验信息的未知环境中凭借所携带的传感器构建所在环境的地图（模型），同时结合已创建的地图对自身进行定位，建图与定位两者密切相关、相互制约。1986 年Smith等［6］提出SLAM 问题起，就吸引了大量的研究者，迄今为止已分别基于滤波器与图优化两种不同的思路提出了多种实现方法［7-8］。

在SALM领域所涉及的重难点问题中，数据关联是其中之一。数据关联源自目标跟踪中的数据融合技术，在SLAM 中用于处理不同时空获得的传感器测量之间，测量与已有地图特征之间的对应关系，以确定它们是否来自共同源的问题，还包括了新特征的确定过程。由于状态估计是SLAM 问题的核心，而数据关联又是状态估计的基础，因此直接影响到最终的定位与建图结果，不准确的数据关联甚至会导致SLAM 的发散［9］。

在SLAM数据关联问题的求解方法中，经典的数据关联方法有最邻近算法（Nearest Neighbor，NN）［10］、多假设跟踪算法（Multi-Hypothesis Tracker，MHT）［11］以及联合相容分枝定界算法（Joint Compatibility Branch and Bound，JCBB）［12］等。JCBB算法主要存在两点不足：①观测数较多时，计算量成指数增加；②当环境干扰因素造成过程不确定增加时，JCBB的关联准确度也会出现明显下降。这是因为JCBB算法是将含有最大配对数目的1 个关联假设作为结果，易出现虽然所有观测都获得了特征匹配，但实际上其中的部分观测却是新特征或虚警的情况。另一方面，当不确定性较大时，含有最大配对数的关联假设往往不止一个［13］，但JCBB 算法仅从其中选择最先得到那个关联假设作为结果，也易引起误关联。目前，对JCBB算法的各种改进［14-15］，如快速JCBB（FJCBB）算法等，主要是围绕前者，即解决计算复杂度问题，而有关提升JCBB算法关联准确度的研究则较少。

随着机器人实际使用环境的日益复杂化，环境中各种不确定因素的干扰等进一步加大，需要建立更为有效的SLAM 数据关联方法。为此，本文将JCBB 算法融入到MHT的框架之下，吸取两种算法的优点，提出了一种多假设联合相容分支定界算法（Multi-Hypothesis Joint Compatibility Branch and Bound，MHJCBB）。与NN、JCBB 等算法每个时刻只保留了1个最优关联假设不同，MHJCBB 算法在实施数据关联时，保留了多个联合相容的关联结果，形成多个机器人航迹假设分支，并计算每个航迹假设分支得分。为减少计算量保证计算效率，将得分较低的假设分支在剪枝过程中去除，而得分最高的假设分支则被选择输出。试验结果证明了MHJCBB方法的有效性。

1 扩展卡尔曼滤波的SLAM建模

采用经典的基于扩展卡尔曼滤波（Extended Kalman Filter，EKF）方法求解SLAM问题。

定义系统在时刻k的状态变量

式中：Xvk＝［xvkyvkΦvk］T，其中的分量分别为机器人的位置坐标与姿态角；

其中的分量分别为各地图特征的位置坐标，对于静态地图特征，其位置坐标为常值。EKF 假设系统状态为高斯分布，k时刻的状态可用估计均值Xk和协方差Pk来表示，

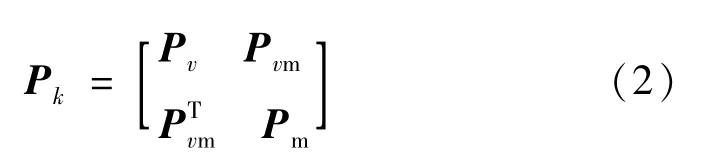
式中：Pv是机器人位置和姿态的估计协方差矩阵；Pm是地图特征位置的估计协方差矩阵；Pvm是机器人位姿和地图特征位置的交叉协方差矩阵。

在使用概率方法求解SLAM 问题时，通常将运动与观测模型按照一个马尔可夫过程来处理，即根据系统前一时刻的状态来预测后一个时刻的状态，与其他历史状态无关，由此可进行递推处理。系统的运动模型描述如下：

式中：fv（·）是非线性函是机器人操纵向量；uk＋1是机器人速度；αk＋1是舵角；wk＋1是高斯白噪声，方差为Qk；Xvk＋1可利用航迹推算得到。

在EKF SLAM 中，利用运动模型进行预测的过程为

观测方程为

式中：b（·）是状态变量Xk的非线性函数；nk是均值为零方差为Rk的高斯噪声。

机器人在获得环境的最新探测数据后，可对状态向量的预测值予以滤波更新：

2 联合相容分枝定界算法

SLAM时，机器人利用自身传感器探测环境，在k时刻，传感器探测得到数据zk，i（i ＝1，2，…，m），假设zk，i来自环境特征Ei。进行关联目的是要确定观测zk，i与地图中已有的特征Fj（j ＝1，2，…，n）的关系，并得到关联假设

将每一个观测zk，i与地图特征Fji配对。如果某个观测是新特征或者虚警，则在Hm中用某个值ji＝0 表示。

假如已有数据关联结果Hm＝｛j1，j2，…，jm｝，联合观测方程为

联合新息及协方差为

式中：

如果联合马氏距离满足

则认为这种关联结果是可接受的，即观测zk可与Hm中相应的地图特征配对。式（12）采用χ2检验，自由度d ＝dim（zk），置信水平为1－α，可取95%可在χ2分布表中查得结果。

Neira等［12］采用联合相容作为关联约束，通过分枝定界搜索算法搜索关联空间，提出了JCBB 方法。JCBB期望每次尽量让每个观测与特征配对成功，它将配对数目单调非减规则作为剪枝策略去除不可能导出最优解的节点，以减少搜索量，并将联合马氏距离最小规则用于启发搜索新节点，优先搜索相容性效果更好的节点，从而保证得到的结果是最优的。

3 多假设联合相容分枝定界算法

3.1 算法的提出

JCBB算法根据所有观测值的综合关联情况来确定关联解，以提高关联的正确率。但在不确定性较多的复杂场合，这种处理方法也易造成误关联，使得关联正确率明显下降。MHT 主要用于处理非常复杂环境下的目标跟踪问题，它将可能的关联情况都作为一种假设分支保留下来，通过多周期的信息积累，来判断那种关联选择是最佳的，并且可以对之前的错误关联进行回溯改正，但计算复杂度高。吸取MHT 算法和JCBB 算法的优点，设计了一种可用于复杂环境中SLAM的数据关联算法MHJCBB。

常规JCBB算法在数据关联时仅保留配对数最大且联合马氏距离最小的1 个关联假设，即使这个关联解是错误的，在后续过程中也无法进行修改。因此，为防止误关联，MHJCBB 算法保留了配对数最大且联合马氏距离最小的NH个关联假设，通过同时维持多个关联假设的方式来保护可能被忽略的最优关联解，以提高数据关联的准确率。NH为常数，实际应用时可根据需要设置。MHJCBB算法的主要步骤为：①机器人位置预测，按式（5）、（6）计算；②进行JCBB 数据关联，保留多个关联假设；③根据关联假设，生成多个机器人航迹假设分支；④按照定义的评价函数，计算航迹假设分支得分；⑤N-Best 剪枝，只保留得分最高的N个假设分支；⑥输出得分最高的航迹假设分支。图1 给出了MHJCBB算法的具体处理流程。

图1 MHJCBB算法流程图

3.2 假设分支的生成

航迹假设分支的生成过程如图2 所示。在k ＝1时刻，保留了NH个关联假设H1，H2，…，HNH，根据关联假设，生成NH条航迹假设分支，对于每条航迹假设分支，在k ＝2 时刻可分别生成NH条航迹假设分支，此时可判断航迹假设分支数目是否超过最大允许值N，如没有，在k ＝3 时刻同理进行分支。如果假设分支数目大于允许的数目N，则需要进行剪枝处理，图中虚线表示已删除的假设分支。

图2 航迹假设分支示意图

3.3 假设分支得分评估

对于每条航迹假设分支，航迹的似然比可以用下式迭代计算：

式中：PD是特征检测概率；PFA是特征虚警概率；pFA是干扰目标的概率密度函数分别表示新息与新息协方差（见式（11））；N（·）表示高斯分布。

采用对数似然比（Log Likelihood Ratio）来表示航迹得分（Track Score）：

因此，航迹得分的递归计算方式为

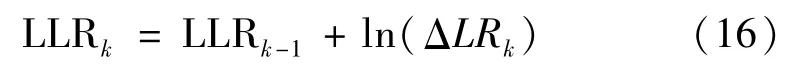
在N-Best剪枝阶段，根据航迹得分的高低，保留得分高的N个航迹假设分支。与MHT 在目标跟踪领域应用时存在多个目标共享观测导致要计算最优假设分支组合的情况不同，MHJCBB不存在组合爆炸问题，因为SLAM 问题类似于单目标跟踪的问题，不存在假设分支相容组合爆炸问题，航迹得分最大的航迹假设分支即为最优假设。

3.4 计算量分析

MHJCBB算法的性能和计算量主要通过以下2 个参数进行控制：关联假设的保留数目NH以及允许保留的最大航迹假设分支数N。一般NH可取2～4，以保证假设关联的多样性。多假设跟踪虽然是延迟决策的方式，但每个时间周期可以输出当前最优的，以保证实时性。

MHJCBB整个算法的计算量最终取决于保留的航迹假设分支数，与航迹假设分支数N 大致成倍数关系。因为形成多个关联假设与常规JCBB 计算量几乎差不多，而航迹得分计算中在JCBB 中也是本来要计算的，所以计算得分不涉及矩阵运算，只增加了对标量按式（16）计算；其次是得分排序，排序的复杂度为O（N2），由于N一般可取10 左右，增加计算量也是很有限的。所以，每条航迹假设分支的计算量与常规的SLAM算法计算量是大致一样的。

另外，需要注意的是，由于状态滤波更新的计算量比较大，可放在N-Best 剪枝后进行，避免对被剪枝的航迹分支进行状态更新。

4 试验与结果分析

4.1 SLAM模型

在SLAM的状态向量中，机器人的位置和姿态可表示为

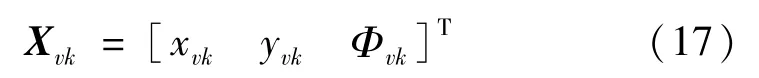
通过航迹推算可获得k时刻机器人位姿的相对变化量

运动方程为

观测方程为

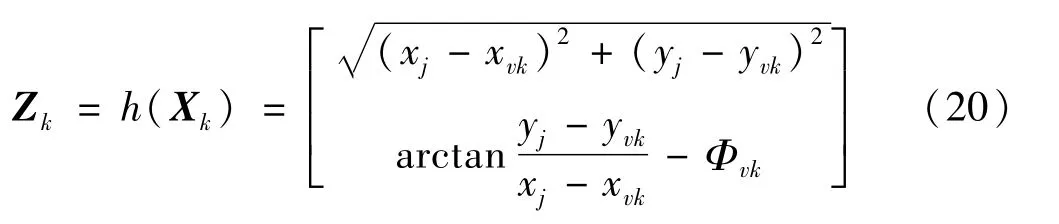
式中，（xj，yj）为特征的平面坐标。

激光雷达的最大量程为4 m，角度探测范围为［－π／2，π／2］。传感器测量均方根误差为σ，其中距离每米的误差为0.01 m，角度误差为0.2°。

4.2 试验结果分析

试验环境为一方形走廊，其中共有168 个静态特征，为模拟实际环境中的运动物体的干扰，假设在该区域内存在10 个处于随机移动状态的物体，物体的移动速度为0.05 m／s，加速度为0.01 m／s2，初始位置随机。移动机器人从（0，0）点开始按逆时针方向匀速穿过该区域，行驶至转角处时机器人以原地转动方式实现90°转弯，每次转弯分10 次完成。图3 给出了试验环境中的特征分布、机器人及干扰物体运动情况，其中：“*”是特征的位置分布；“△”是机器人理论行驶路径；“---”是干扰物体运动轨迹。试验将在不同的测量误差条件下测试数据关联的正确率。

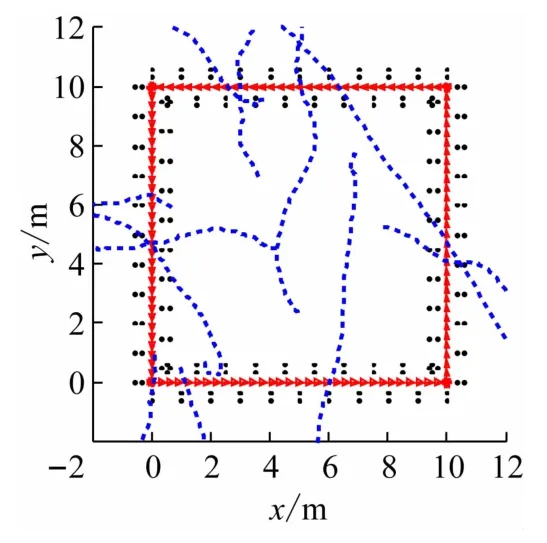
图3 特征分布、机器人理论路径及移动物体轨迹

利用Monte Carlo 方法重复进行20 次试验，并将获得数据进行平均用于比较分析。参数设置如下：PD＝0.9，PFA＝0.05，pFA＝0.1，N ＝12，NH＝2。数据关联准确率定义为该时刻正确配对的观测个数（包括观测与特征正确对应、虚警判别正确两部分）与参与配对的总观测个数的比值。

当测量误差为σ时，NN、JCBB和MHJCBB 3 种方法数据关联正确率的结果对比如图4 所示。图5、6 分别是此时x、y 方向的估计误差比较。从图中可以看出，JCBB和MHJCBB都取得了90%的关联正确率，差别不明显，但是NN由于误差的积累，在后期关联正确率迅速下滑，导致估计误差迅速的增大，SLAM 算法发散。

图4 测量误差为σ时关联正确率比较

图5 测量误差为σ时x方向误差比较

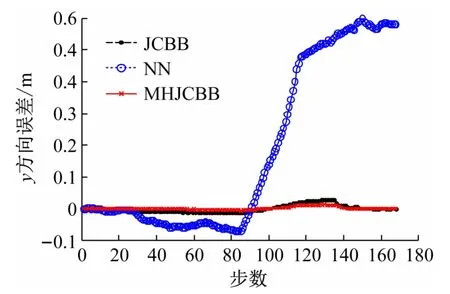
图6 测量误差为σ时y方向误差比较

图7 测量误差为2σ时关联正确率比较

测量误差为2σ时，3 种算法数据关联正确率的比较如图7 所示。可以看出此时MHJCBB 开始体现出优势，尤其在50～130 步之间其关联结果明显优于JCBB算法。进一步增加测量的不确定性，当测量误差达到4σ时，关联正确率的结果对比见图8。从图8 可知，随着测量误差不断增加，JCBB 的关联正确率会突然下降，类似于图4 中NN 的表现，很容易造成SLAM 算法的发散。但是MHJCBB却保持了较好的性能，正确率都在0.72 以上，而JCBB 后期接近于0.42，MHJCBB 优势明显。

图8 测量误差为4σ时关联正确率比较

试验结果表明，传感器测量误差的增大，会引起整个处理过程不确定性的增加，此时NN、JCBB算法的关联准确率都会随之下降，易造成观测与特征之间的配对出错，影响机器人的位姿估计，并使得所建立的地图不确定性增加，甚至会导致SLAM 算法的发散。而MHJCBB算法则通过保留多个航迹假设分支，获得了较好的稳定性和可靠性。

5 结语

数据关联问题的求解是SLAM研究领域中的关键难点之一，尤其对于经常使用的经典滤波算法如卡尔曼滤波等，少数的几次误关联便容易导致算法的发散。JCBB算法是SLAM数据关联时广泛使用且行之有效的一种数据关联方法，但当环境中的不确定性增加时，其关联正确率将会出现明显下降。文中将多假设跟踪（MHT）算法与JCBB 算法的优点有机结合，提出了一种基于多假设跟踪的MHJCBB。该算法的主要具有如下特征：①每次关联时保留多个联合相容关联假设，形成多个机器人航迹假设分支；②为每个航迹分支定义了评价函数；③依据评价函数，通过剪枝过程，将机器人航迹限制在一定数量内。理论分析与试验结果表明，与经典NN、JCBB等算法相比，在不确定性较大时，MHJCBB算法仍能获得稳定可靠的数据关联结果。