热传导方程解的梯度估计和解析性*
邢家省,杨义川,吴 桑
(1.北京航空航天大学数学科学学院,北京 100191;2.数学、信息与行为教育部重点实验室,北京 100191)
热传导方程的解是解析函数,这是热传导方程的一个深刻的结果,在偏微分方程的研究中起着重要作用[1-10].奥列尼克[2]对热传导方程解的各阶偏导数给出了先验估计,证明了热传导方程的解是解析函数.该结果是关于空间变量局部解析的.笔者将对热传导方程初值问题的解关于空间变量和时间变量是解析函数这一结论给出简单的证明,并指出定解条件不同会导致解析性结果不同.
1 n维齐次热传导方程初值问题的解是解析函数的证明
考察n维齐次热传导方程初值问题
(1)
其中:x=(x1,x2,…,xn);Δu=ux1x1+ux2x2+…+uxnxn.利用Fourier变换法,可以得到n维齐次热传导方程初值问题的求解公式[1-10]
(2)

引理1[1]设φ(y)∈C(Rn),且φ在Rn上有界,
(3)
则对于Ret>0,u(z,t)是关于所有复变量z∈Cn,t∈C的解析函数.
证明设复向量z=ξ+iη,复数t=σ+iτ,其中ξ,η为n维实向量,σ,τ为实数.

从而对于σ>0,有

同理可证
关于复变量z,t在{(z,t)∈Cn×C,Ret>0}上是内闭一致收敛的.

由引理1可得以下结果:
定理1设φ(y)∈C(Rn),且φ在Rn上有界,则由(2)式确定的函数u(x,t)在Rn×(0,+∞)上关于(x,t)是解析的.
注意到

定理2设φ(x)∈C(Rn),且存在常数|φ(x)|≤A+Ber|x|,使得|φ(x)|≤A+Ber|x|(x∈Rn),则由(3)式确定的函数u(x,t)(u(x,t)∈C(Rn×[0,+∞))∩C2,1(Rn×(0,+∞)))是问题(1)在Rn×(0,+∞)上的古典解,且u(x,t)∈C∞(Rn×(0,+∞)),对于t>0,u(x,t)是x的整解析函数.

2 热传导方程解的偏导数估计

(4)
其中C=2n+10.

由极值原理[1-7]可推出在wR+ρ中,
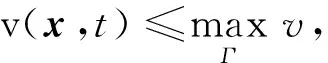
(5)
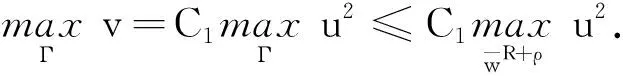
于是
(6)
由此为了证明(4)式,只需证明在wR+ρ中对于适当选择的C1,有Lv≤0.
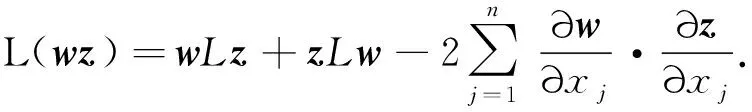
L(((R+ρ)2-(|x|2+|t|))2)=2(2n+1)((R+ρ)2-(|x|2+|t|))-8|x|2=q(x,t),
于是
(7)
为了估计(7)式等号右边的第3个和式,应用估计式2ab≤a2+b2,可得
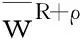
奥列尼克[2]应用(4)式进一步建立了热传导方程解的任意阶导数的估计:

(8)

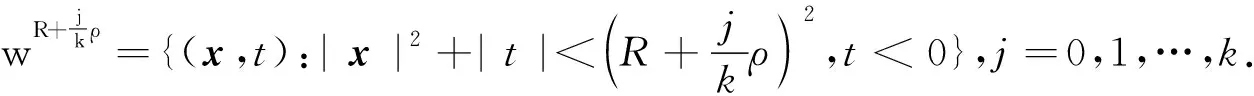

(9)
从j=0开始,依次将j=1,…,k-1的情形代入(9)式,得到一系列的迭代不等式,由此可得(8)式.证毕.

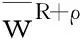
(10)
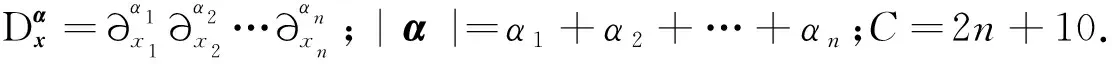

由此推出(10)式成立.证毕.
3 热传导方程的解关于空间变量x的解析性

由牛顿二项式定理可得引理6.
引理7[1-2,10-14]对于任意正整数m,有mm≤m!em.

引理8[2]方程Lu=0在区域w中C2,1(w)类的解u(x,t)是变量(x1,x2,…,xn)的解析函数,即对于任意的点(x0,t0)∈w,当|x-x0|<ε时,函数u(x,t0)可表示为按xj-x0j(j=1,…,n)的幂的形状的收敛幂级数,其中ε=ε(x0,t0)>0.
证明根据文献[1-2]中的结果,函数u(x,t)是w中x与t的无穷次可微函数,则由泰勒公式,有
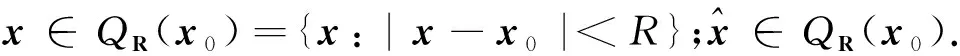
应用引理4中u(x,t)导数的估计,选取R+ρ足够小,使得区域wR+ρ含于w,其中wR+ρ={(x,t):|x-x0|2+|t-t0|<(R+ρ)2,t 注1[1-2]在Rn+1的某个区域Q中,满足齐次热传导方程的函数u(x,t)关于t不一定是解析的. 例如,任取x0∈RN,t0∈R,构造函数 在齐次边值条件下,邢家省等[15]证明了齐次热传导方程初边值问题的解关于(x,t)可展开成收敛的幂级数,即热传导方程初边值问题的解关于(x,t)是解析的. 引理9[2](刘维尔定理) 设在半空间QT={(x,t):x∈Rn,t≤T}中给定了方程Lu=0的C2,1(QT)类的解u(x,t),并设 (11) 其中C1,q为正常数.那么,u(x,t)在QT中是幂次不高于[q]的关于x,t的多项式,更准确地,在QT中, (12) 证明为了证明(12)式,只需证明u(x,t)的所有形如 (13) 的导数在QT中恒等于0. (14) 其中常数C2与ρ无关.显然,当k+2p>q时,(14)式的右端当ρ→+∞时趋于0.如果|α|+2p≥[q]+1,那么|α|+2p>q,所以所有形如(13)式的导数在wR中等于0.因为R是任意数,所以在QT中这些导数等于0.证毕. 特别地,由引理9可以推出,方程Lu=0在下半空间QT={(x,t):x∈Rn,t≤T}中的有界解u(x,t),在这个下半空间是常数[2].注意,方程Lu=0在上半空间Q={(x,t):x∈Rn,t>0}中的有界解未必是常数. 对于调和方程的解,有学者[1-2,4]利用平均值定理给出了梯度估计,进而给出了高阶偏导数的估计,由此证明了调和方程的解是解析函数.而调和方程Δu=0的解u(x)可以看作是热传导方程Lu=0的解,于是利用热传导方程的结果,也可推出调和方程的解是解析函数.此外,调和方程的解可以通过构造辅助函数,利用极值原理,从而给出梯度估计.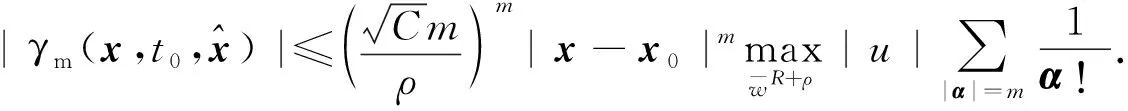
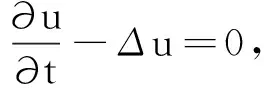
4 热传导方程解的刘维尔定理



