渐进式流水线脉冲解交织技术研究

熊朝廷 黎 亮

（四川九洲电器集团有限责任公司，绵阳 621000）

无线电技术从诞生之日至今，已经在各行各业得到广泛应用，从日常生活中常用的手机通信、卫星广播到军事运用的一次雷达、二次雷达、无线电通信导航等，应用种类繁多、涉及领域颇广。其中无论是哪一种应用，都面临着提高通信质量、传输带宽及传输效率等需求。根据这些需求，研究人员又研发出各种各样的信息传输、信道传输、加解密、纠检错等技术，以满足日益增长的用户需求。由于这些技术需求所产生的无线电信号都必须在空间中传播，因此由反射、折射所产生的多径信号或多节点所产生的同步或异步干扰就必然存在；如果多径信号或干扰信号在时间上能错开，在信号解码层级就能进行正确的解码，仅需在数据处理层面采用一些手段进行剔除；反之如果多径信号或干扰信号在时间上不能错开，就会存在一定程度的交叠，形成较长的目标脉冲串，对信号层级的解码能力形成挑战，这种信号就被称为交织信号。交织信号在无线电技术中经常出现，对于某种应用或某个系统，解交织的能力直接影响系统的性能，值得进行深入研究。本文针对严重交织信号的解交织处理展开研究，包括脉压后对消改进、增加对消峰值的修正处理，以及渐进流水线处理结构的设计。

1 迭代处理设计

对于二次雷达系统，典型应答信号由多种编码不同、幅度相同的扩频脉冲构成。多目标产生的应答信号在空间进行合成，在应答机接收端包含多个来自不同应答机的应答信号，这些信号具有不同的幅度、时延和初始相位。对于密集应答目标，各应答信号的脉冲波形普遍存在不同程度的交叠（交织），从而形成一个复杂的组合信号。

二次雷达系统中询问端对应答端发出的应答信号进行处理，一般的处理方式选择了无信号交织的高斯噪声背景理想条件下的最优检测方式。因此，在多目标条件下，交织信号已经偏离了传统处理的假设条件，使传统处理性能受到严重影响。

为了使对消能够达到尽可能抑制旁瓣干扰的效果，采用基于CLEAN 算法且由迭代处理构成的解交织处理方法，每次迭代包含对脉冲的检测、对消和修正。每个检测单元上的脉冲压缩能够在相邻距离单元脉冲检测结果的基础上进行反复优化，其基本处理流程如图1 所示。

图1 基于对消的解交织算法流程

图1 中，匹配滤波使用了多种脉压波形作为参考，对每种脉冲分别进行脉压处理；经过脉冲压缩后，脉冲检测对其中超过检测门限的脉压峰值进行判断并输出；检测结果同时作为先决条件并利用各参考脉压波形重构自相关旁瓣和互相关旁瓣干扰信号；匹配滤波结果随即使用重构信号进行旁瓣对消，并将对消后的结果重新进行脉冲检测，从而在减少旁瓣干扰的条件下提高已经检测到的脉冲精度，以及对之前被旁瓣遮蔽的脉冲峰值的检测精度。

基于CLEAN 算法中对消处理对识别信号具有较强的适用性，该处理是根据估计的相关峰值用参考信号合成一个信号，用于尽可能抵消原始数据中与该相关峰对应的信号分量，从而在再次的匹配滤波和峰值检测中抑制该信号对其他峰值检测产生的影响。

2 脉压后对消处理算法

脉压后对消处理的目的与现有对消相同，其优势在于可以在处理流程的循环环节节省脉冲压缩步骤，从而减少系统计算开销，提高处理速度。

将脉冲信号s=[s0,s1,…,sN]H表示为一个采样点数为N 的波形，实际接收信号经过匹配滤波后可以表示为：

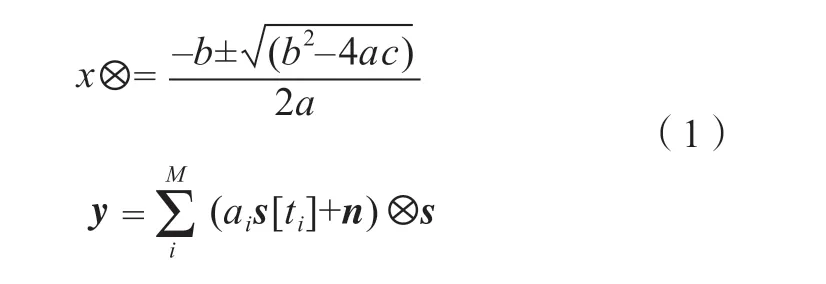
式中，n 表示接收机噪声；ai是该接收信号中第i 个脉冲对应的复幅度；ti是该脉冲的时延；s[ti]表示延时为ti条件下的脉冲波形； 为N 元带圆圈乘运算。原始CLEAN 对消算法针对第i 个脉冲的脉压前对消再进行匹配滤波的过程，可以用公式表示为：

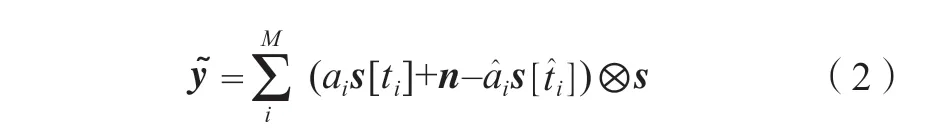
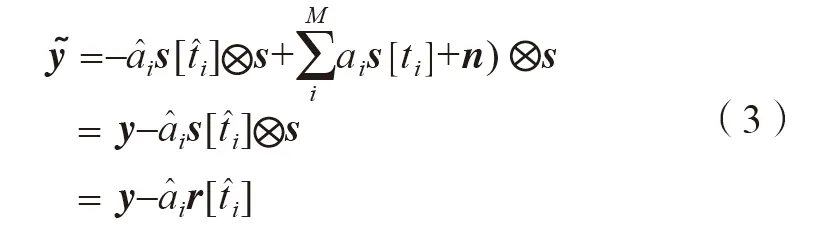
用仿真生成某个包含18 个时延相近的应答信号的接收信号片段，通过对比可知解交织处理的性能和效果。其中每个应答信号由两个间隔固定、编码不同的脉冲组成，因此脉冲检测包含两组结果。传统处理的匹配滤波对两种脉冲的处理结果和在此基础上达到的脉冲检测效果如图2 所示。其中，黑点表示真实脉冲对应的时延和幅度，红线表示基于平均能量的检测门限，红圈表示检测到的脉冲。

从匹配滤波输出可见，脉冲压缩产生的峰值和旁瓣抬高了检测门限，导致在较强信号附近的脉压峰值检测存在困难。

从脉冲检测结果可见，交织引起了明显的脉冲漏检测，脉冲1 漏检11 个，约占60%；脉冲2 漏检5 个，约占28%，检测到的脉冲通过组合能够得到的完整应答信号只有6 个。

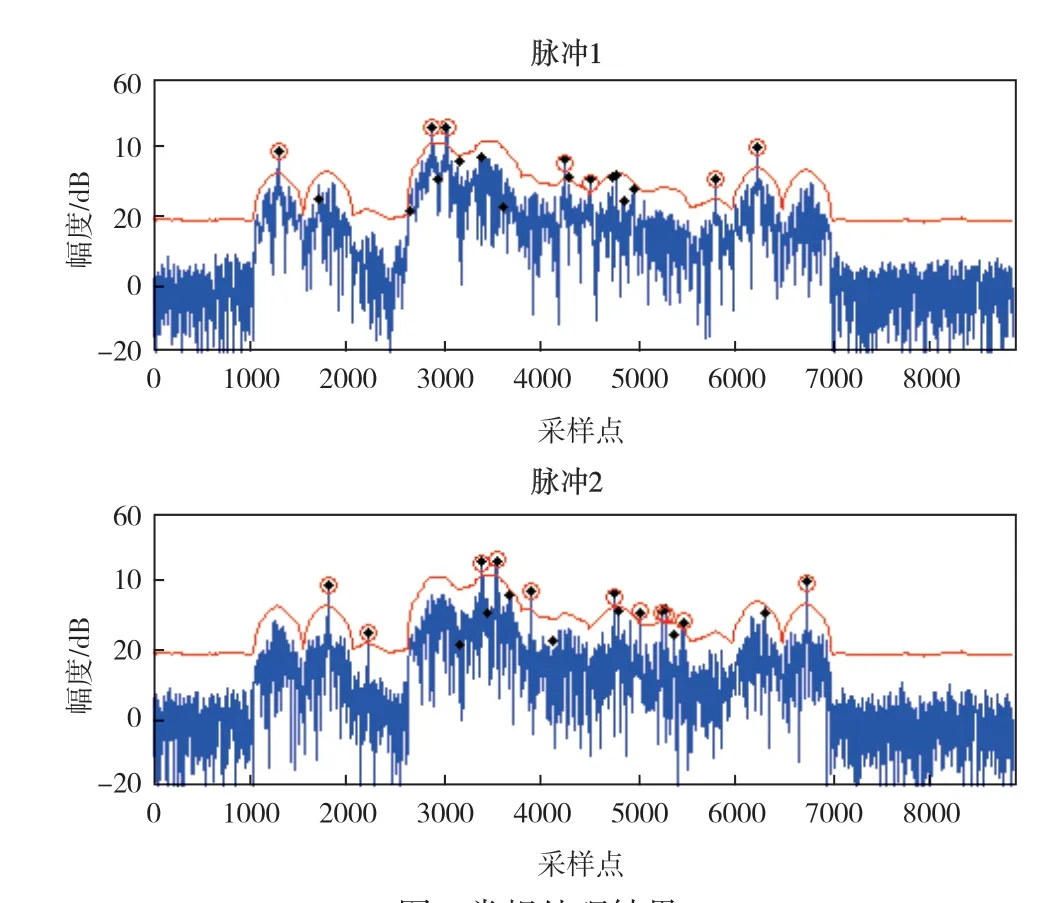
图2 常规处理结果

结合CLEAN 算法的解交织处理结果如图3 所示。从仿真结果可见，解交织处理明显改善了应答信号片段中两种脉冲压缩的旁瓣影响，使大量小幅度的脉压峰值也能超过检测门限，从而达到较好的脉冲检测效果。仿真结果表明，解交织处理具有明显提高信号脉冲检测性能的作用。

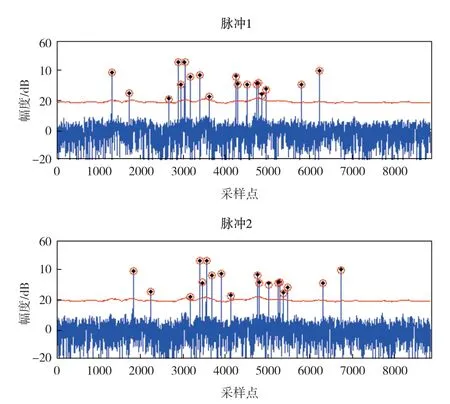
图3 解交织处理结果

3 基于最小二乘法的峰值修正方法

峰值矢量修正是利用了最小二乘法原理，对多个峰值进行进一步幅度和相位的校准，以满足后续测角处理对脉冲参数精度的要求。峰值适量修正处于解交织处理流程中对消环节，如图4 所示。

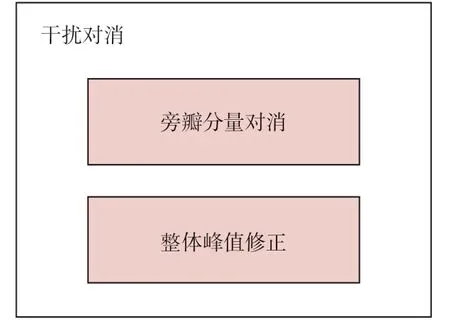
图4 峰值修正处理与整体流程的关系

将接收信号表示成矩阵形式为：

式中，M 为该接收信号片段中包含的脉冲数量。当获得了该接收信号片段中各脉冲时延估计后，用代替上式[s[ti],s[t2],…,s[tM]]中的ti，并表示为，则上述方程可以近似为：

因此对于含有M 个脉冲相关峰片段的修正处理，需要进行一个M阶矩阵求逆运算。

以M=2 为例，仿真对某信号经过匹配滤波检测到了两个峰值，然后利用对这两个峰值的时延估计进行修正处理，如图5 所示。

图5 峰值矢量修正效果

从仿真结果可知，经过修正后，匹配滤波峰值上的误差减小，与真实幅度接近，表明了修正处理的有效性。

4 渐进流水线处理结构设计

本技术研究采用流水线结构替代解交织算法中的整体迭代处理，一种对3 次迭代的流水线设计如图6 所示。

从图6 可以看出，沿着脉压输出时间序列上设计4 个并行处理指针并参考波形宽度等间隔分布。其中，每个处理指针对所在的脉压序列单元进行相关峰检测和旁瓣对消，并同步逐个推进采样单元。处理指针1 所在的脉压序列单元与处理指针0 进行旁瓣对消的作用范围相邻，因此处理指针1 总是对处理指针0 进行了旁瓣对消后的结果进行检测，从而可以补充弱相关峰的检测精度或改善强相关峰的参数估计精度。处理指针2 和处理指针3 的原理与之相同，于是每个脉压序列会经历3 次对消和4 次检测，以使其能够达到与3 次整体迭代处理相近的效果。基于渐进峰值修正处理的流程如图7 所示。

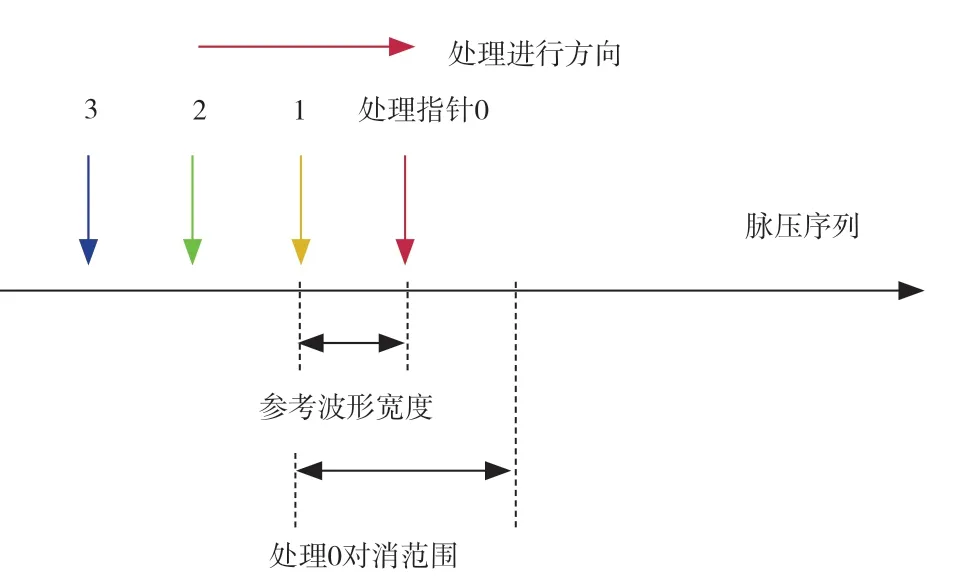
图6 流水线处理示意图

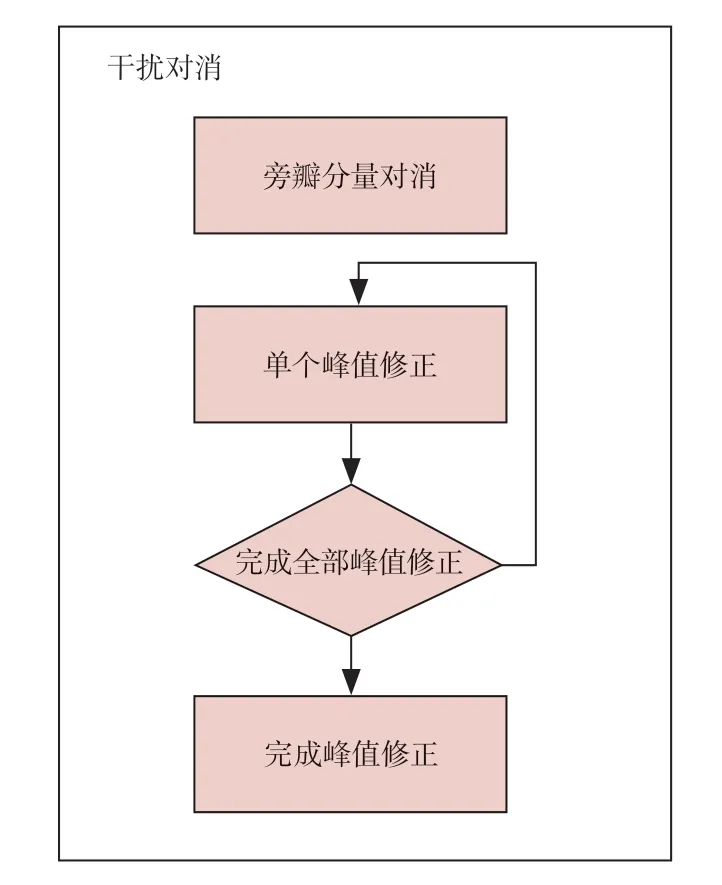
图7 渐进峰值修正处理流程图

图8 峰值矢量修正效果

以M=2 为例，仿真对某信号经过含有渐进峰值修正的对消处理结果如图8 所示。仿真结果表明，经过处理后，对脉冲相关峰峰值的估计结果与真实幅度接近，表明了修正处理的有效性。

5 结 语

本文对严重交织信号的解交织处理展开了研究，包括脉压后对消算法的改进、增加对消峰值修正处理算法，以及提出了渐进流水线处理结构的技术。渐进流水线处理结构技术采用的渐进峰值修正处理，将原有提高峰值估计精度的矢量修正处理移动到寻找峰值的循环中简化进行，是一种利于算法工程实现的优化措施。该设计可以将涉及复杂矩阵求逆运算的矢量修正处理过程转化为迭代形式的简单处理，从而达到减小系统设计难度的目的。但若要将该技术在工程上实现，还需要在现有技术水平上，细化仿真分析、归纳多种条件下的处理性能、优化算法设计，同时还要考虑实装设备对实时性的要求及硬件资源受限等限制条件。