数学形象思维能力的培养策略

林翠英

摘  要：从思维的抽象性角度来看，思维可以分为直观行为思维、具体形象思维和抽象逻辑思维三种。不少教师在发展学生的抽象逻辑思维能力上花费了不少精力，但效果甚微。究其主要原因还在于前期没有形成良好的具体形象思维能力。文章就如何培养学生的数学形象思维能力展开分析。

关键词：形象思维;表象;直感;想象

思维指人体接受、储存、加工以及输出信息的过程，是人脑对客观事物的内部规律或本质属性的反映。随着教育改革的推进，发展学生的抽象逻辑思维是很多一线教师不断努力的方向，而忽略了培养学生的形象思维是获得抽象逻辑思维能力的基础，更符合小学生的认知规律。因此，我们教师应从思想和行动上重视形象思维能力的培养，这是发展学生思维能力本身的需求，也是提高课堂效率，发展学生数学思维的需要。

一、丰富表象，夯实基础

所谓的“表象”是以往感知过的客观事物在人脑再次出现，是形象思维形成的基础。心理学家研究发现视觉系统是人类获取信息的主要途径，要丰富表象的累积，可提供如挂图、实物、模型等物品，让学生通过观察获取表象信息 [1]。感知是数学表象的根本，丰富的感知能形成高概括性的表象。这需要教师引导学生通过多形式、多方位、多系统地参与、观察或操作数学现象，构建丰富的数学表象，夯实思维发展的基础。

例1：“9+几”的教学。

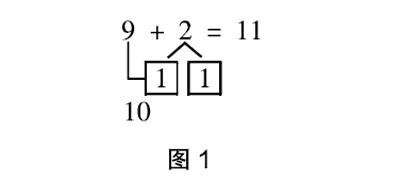
问题：框内有9只球，框外有2只球，一共有多少只球？

教师根据这道题，提前准备道具引导学生动手操作把框外的一只球放到框内，此时框内有10只球，框外有1只球，合计11只球，这是最原始阶段的直观行为思维。若想进一步建立具体的形象思维，教师可引导学生思考：9只球加上2只球，一共是11只球。换成算式应该怎样计算呢？这里是把两只球怎么分的，分别与谁搭档而得出结论？学生经思考后得出以下分解式（见图1），这是直观行为思维向具体形象思维转变的过程，也是小学低年级数学课堂教学常用的方法，这种方法借助外化了的图式表象，能举一反三地推导出20以内的进位加法法则。

由此可見，数学课堂教学过程中进行直观演示操作后，学生虽然能解决题干中的问题，但思维发展仅局限于直观阶段。若通过图式表象去揭示问题的内涵，学生就能理解问题的本质并产生解决同一类问题的能力。因此，教师可通过图式表象的方法，引导学生从直观思维转变到具体形象思维，逐渐形成空间概念。

二、关注直感，增加数学想象

所谓的“直感”是指人体对具体事物的感受。数学直感可归纳为模式补形直感、形象识别直感、象质转换直感和形象相似直感四类，小学生以形象识别直感和模式补形直感为主，他们判断一个数学形象时不必以语言和概念为中介，只需调动大脑中原有的一般表象与对应物进行对比即可。

1. 形象识别直感的训练

所谓的“形象识别直感”是指用数学基础表象的类象与具体对象的个别现象进行比较，再根据两者特征的相似性来判断个象与类象是不是同质的思维方式。学生这种直感能力体现在对各类图式、图形的变式的再认。因此，教师在课堂教学中应关注学生的形象识别直感，通过反复多次训练学生的变式、变图能力，以提高他们的数学想象力。

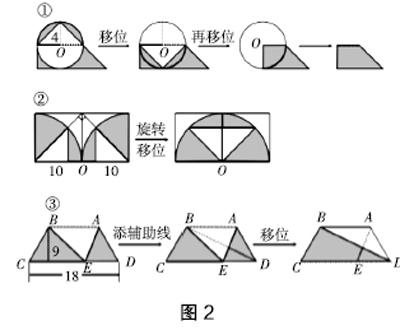
例2：求下列图形（见图2）阴影部分的面积。（单位：米）

此题需学生从复杂的图里识别到与一般图形同质的形象特征，将复杂的图形通过旋转、移位或添加辅助线等方式分解出学生所熟悉的基本图形，图形在大脑中运动变化成基本图形后，学生快速识别且计算出阴影部分的面积。这种方法需建立在学生对基本图形熟识的基础上，多次训练可增加形象识别直感的熟练度。

2. 模式补形直感的训练

所谓的“模式补形直感”是运用大脑已形成的表象模式对图形部分特征一样的内容进行表象补形、整合的思维形式。根据小学生的思维特征，常将补形法的思维机制运用于解决问题，以增强学习者的想象力。

例3：求下列图形（见图3）的周长。（单位：米）

这组图形周长的计算，同样需要教师引导学生从不规则的图形里寻找出与基本图形的同质特征，通过移动不规则图形的线段，将残缺不规整的图形补充成规整的学生所熟悉的图形，便于学生快速识别并计算出图形的周长。这是典型的使用模式补形直感的方式解决数学问题，学生在线段的等价变换中将复杂的问题简单化，熟练掌握这种方法能帮助学生形成丰富的表象模式，更好地解决更多的数学问题。

三、发挥想象，突破自我

爱因斯坦曾经说过：“比知识更重要的是想象力，它是知识进化的源泉，是科学研究的重要因素。”想象作为一种特殊的思维形式，是大脑突破时空束缚，将原储存的表象进行加工和改造产生新表象的过程 [2]。表象是想象的原材料，直感是想象的基本手段，当表象与直感在人脑中有机联合就形成新的形象。数学想象是学生创造性思维形成的必需品，离开想象就失去了创造的灵感。从其内容形式角度来看，有图形和图式两类想象;从它的独立性角度和新颖性来看，有创造性和再创造性两类想象 [3]。发展小学生的想象能力，可理论联系实际从生活实中寻找合适的素材，引导学生将理论的数学和实际的生活联系在一起思考问题。

例4：“圆的认识”，在各种场景下画圆。

师：同学们都已经学会了怎样用圆规在本子上画圆，现在老师想在黑板上画一个圆，没有带大圆规怎么办呢？

生：把呼啦圈扣在黑板上，用粉笔沿边画一圈。

师：这方法好，如果我们想在教室里画个中心圆，你们有什么办法吗？

生：我看到过体育老师画投掷实心球的圈，人站在中间为圆心，手上持装有白灰的大勺子，保持手臂姿势的固定，人边旋转边让勺子里的白灰洒在地上，当一圈儿转完，圆就画成了。

师：这位同学观察得非常仔细，值得表扬。如果我们想要挖一个圆形的鱼池，有什么办法画圆呢？

生：取一根足够长的绳子，固定一端，另一端绕地一圈儿，就能获得圆形的鱼池了。

师：这个方法不错，如果要在我们这个区建造一条圆形的环城高架，大家觉得有什么办法画这个大圆呢？（教室瞬间安静下来）

生（底气不足地说）：在中心点放置一台信号发射机，给在圆边上的坦克发送信号，塔克沿着信号开一圈。

师：想法不错，问题是遇到房屋等阻碍物怎么办呢？

生：用飞机，边开边撒白石灰。

（其他学生七嘴八舌地表示这个方法不可行，石灰会污染环境还会被风吹得到处都是，不能画成圆）

师：想想我们的设计师是怎样做到的呢？

生：我知道了，只要在区域地图上画一个圆就行了，在圆边上的建筑物可以拆迁，遇到河流可以修桥。

（话音刚落，掌声就响起来了）

这是一个引导学生根据生活展开想象的真实案例，教师引导学生从画小圆开始，逐渐放大圆的面积，直至无法人为地去画为止。学生在此过程中不断突破原有的空间束缚，对画圆的方法不断进行加工改造，直至新的方法产生，这也是学生通过想象挑战自我，突破自我的表现。

综上所述，发展小学生的数学思维能力首先要培养他们的形象思维，教师可挖掘教材和生活中的素材，从直观、表象和想象三个方面有意识地引导学生，将培养学生的数学形象思维渗透到课堂教学的各个环节，为促使学生形成更高级的抽象逻辑思维夯实基础。

参考文献：

[1]  任樟辉. 数学思维论[M]. 南宁：广西教育出版社，1996.

[2]  郭思乐. 数学思维教育论[M]. 上海：上海教育出版社，1997.

[3]  吴球. 小学数学教学中对学生逻辑思维能力的培养探究[J]. 学周刊，2012（23）.