基于问题设计的研究导向型教学在《复变函数》课程中的应用

刘方红 曹秀娟

摘要：综述研究导向型教学理念在大学数学课程中的应用研究，梳理出该教学模式应用中“问题设置的重要性”，进而分析探讨了教学各环节的注意要点。以复积分的计算和拉普拉斯逆变换的求解两个知识点的教学实践为例，探索基于问题设计的研究导向型教学在《复变函数》教学中的应用。

关键词：问题导向 研究型 复积分 拉普拉斯逆变换

新的教学改革目标越来越清晰，就是要更好的培养学生解决问题的能力，而不仅仅是知识的存储器。这势必对教学理念方式提出更新变革的要求。将研究型教学理念运用到大学本科课程教学中，可以说是一种全新的教学理念的创新，也是一种探索。“研究型学习是以问题探究为主要特征的学习”。数学作为解决问题、课题研究的工具学科，以《复变函数》为例，在工程领域有广泛的应用，其学科特点要求课程教学过程中更需要通过教学改革理念革新教学思路、方式，通过课堂教学流程再造，以切实培养学生研究解决问题的能力。

一、研究型教学综述

在大学本科课程教学中借助研究型教学模式提升教学效果，首先要使“教”与“学”的主体双方就该种理念模式有个统一的认识，形成建构知识的“学习共同体”。“教”与“学”的主体双方只有基于共同认知，才能快速进入课堂角色，使先进的教学理念发挥有效的作用，达到教学改革目标。

目前，有学者从研究型教学在高等数学课程教学中的应用着手，做了较系统的理论分析和实践探索。孙会霞、陈红如探索将“以问题为导向的大学数学课程教学模式”应用在微积分中“定积分的概念”的教学实践中，并提出了教学过程中各个环节的具体内容及要点。刘晓妍、王言英探索将“问题驱动式教学模式”应用在高等数学的教学实践中，通过问题的巧妙设计，驱动了“中值定理”教学过程，取得了较好的教学效果。王芬玲、樊明智通过分析复变函数教学中存在的问题，说明了复变函数教学中采用研究性教学的必要性，并在教学过程中探索实践。

综上研究成果发现，研究型学习是以问题探究为主要特征的学习。研究型教学模式同传统教学模式的最大区别是，其以问题为起点，将问题探究过程作为教学的主线，课程教学过程就是教师遵循“提出问题、分析问题、研究问题、解决问题”的框架路线，引导学生开展研究型工作，培养学生自主运用旧知识构建发现新知识的教与学的过程。那么，我们教师可以参考研究生论文指导过程，站在导师而非讲师的角度，引导学生的学习。遵循教学指导的工作路线为：选题，基础知识综述，研究型教学，答辩式考核。

二、基于问题导向的研究型教学各环节的注意要点

（一）问题导向，合理选题。在充分的学情分析的基础上，选题

问题的质量更大程度上决定了课程教学的质量。来自不同专业方向的学生，因其不同的专业知识储备，对该模式的接受程度是不一样的。学生既有的知识体系和解决问题的基础能力决定了“选题”的方向和角度。选题对数学基础较薄弱的学生、对整个教学过程效果起到了重大作用。兴趣是最好的老师。在研究型教学中，尤其要注意借助兴趣的力量将未知带给学生的压力转化为学生求知、探索的动力。故，问题设计要额外注意发挥激起学生开启数学思维的兴趣的作用。

（二）开放式研究、教学筹备，必需储备基础的知识和技能。教师全面深入备课，学生提前预习

开展研究工作的前提要准备相关的知识作为思考基础，相关的研究工具作为支撑。研究过程充满不确定性，尤其对于知识面并不宽广的学生，要在研究学习开始之前储备相应的知识和技能，避免研究思路脱节，陷入低级的知识圈而得不到突破。另一方面，教师也要更加锻炼一种解答学生提出各种问题的能力，或者要具备一种提前预判学生研究方向偏差常见问题的能力，通过连续的正确分析和解答学生的提问，以达到引导学生在解决问题的道路上不断沿着正确的方向前进，更加深入进新的知识领域，实现知识的总结和提升，取得研究的成果，完成教学任务。这必然要求教师要加强自身知识和经验的积累，全面深入的备课，制定更加有针对性，预判性的教学方案。

（三）引导研究、教学，做教学管理者

做到对研究教学过程进行有效引导和管控，是研究型教学中对教师提出的新要求，而不能只停留在三尺讲台侃侃而谈式的灌输知识。站在管理学的角度，可以把前述“选题”和“筹备”两个环节视为“设定目标”和“编制计划”，那么“有效引导和管控”就应该被深入理解为“检查并纠偏”。要想通过充满不确定性的开放式研究过程，实现既定的教学目标任务，就务必要加强对研究过程的管控。要发挥教师的专业能力，及时有效的引导学生的研究思路，重点关注研究过程的难点，管控学生的研究状态，避免因研究工作的困难或繁琐而影响学生的研究兴趣，帮助学生调动研究学习的热情和效率。教师要树立不仅要“言传身教”却更要“用心经营管理课堂”的教学理念。

考虑到开放式研究性工作在时间和空间上的延续性特点，决定了学生参与课堂活动开展研究性学习之余，必然要在课后接续研究思路，应具备利用一切可用的时间和资源，主动思考钻研的品质，只有如此多要素投入才是真正的“搞研究”，才会有成果、有所得，达到研究型教学的效果。所以说，教师要注意做课堂的管理者，同时又不能仅局限于教室课堂一隅，需注意搭建开发“第二课堂”，将研究型学习向学生的生活学习的各个空间、时间延伸。

（四）考核方式，（分组）总结答辩

同全新的教学模式配套，针对研究型学习效果的评价考核必然要改造传统的教学考核方式。着眼于在实践应用层面将该教学理念模式的推向深入，即时收获有指导意义的研究成果。基于问题导向的研究型教学模式中，对学生的成绩评定需综合其多方面表现，并侧重其过程中的行为评价考核。具体评价内容和指标应主要包含学生的研究型学习成果质量、教学参与程度和团队合作能力三大方面。遵循教学指导的工作路线，该教学模式下最终产生的成果形式应是问题研究书面报告或者论文，并通过课堂答辯形式表现。确保评价指标构成及评价办法全面反映学生的综合素质水平。

三、基于问题设计的研究导向型教学在《复变函数》教学中的应用探索

总结个人教学实践经验，下面以复积分的计算和拉普拉斯逆变换两个知识点的教学为例，探索基于问题导向的研究型教学在《复变函数》教学中的应用。

（一）复积分的计算

1.学情分析，问题设定

教材中在不同章节给出了复积分的计算方法，但方法之间的联系与区别没有给出详细的对比分析，不同方法求解问题的效率是不同的。为此给出以下问题，启发学生从熟悉的知识点上探究出新问题，更好的理解知识点，找到多种解题方法及不同方法适用的问题类型。从而培养学生自己整理归纳知识点的好习惯。

计算下列积分

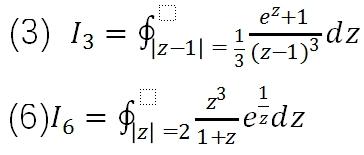
2.教学准备

将班级学生分成6个学习小组，课前复习柯西积分公式、高阶导数公式及留数计算的相关知识，为解决具体问题做准备。每个小组任选三题进行求解，求解过程中注意方法的选择和知识点的运用。

3.课堂管理

分析问题，探索求解。各小组对自己选择的题目给出具体求解过程，归纳总结出问题求解的方法。

对比分析，总结反思。根据闭曲线内奇点的类型，如果奇点是可去奇点或者极点，应用Cauchy积分公式、高阶导数公式和留数定理在本质上是一样的，比如（1）（2）（3）题，此时应用Cauchy积分公式或高阶导数公式更简洁，因为不需要判别极点的阶数。但当奇点是本性奇点时比如题（5），要应用留数定理进行求解，留数定理可以求解的问题范围更广。如果曲线内有多个奇点时，用留数定理比应用复合闭路定理更方便。当在有限孤立奇点处的留数不容易计算时如题（6），可以借助无穷远点的留数的性质及规则进行计算。

4.学习效果评价考核

引导学生讨论分析不同求解方法之间的区别和联系及各自的优缺点，使学生对求积分的方式方法加深了理解，取得了较好的教学效果。

（二）拉普拉斯逆变换

拉普拉斯变换在工程领域有广泛的应用，比如在信号与系统中，是研究线性系统的重要工具。在求解线性微分方程中也有着很好的应用。在拉普拉斯逆变换的求解中，考虑上一堂一题多解的综合课，引导学生进行多角度多方位的思考，通过分析-综合-再分析-再综合的方法，培养学生应用不同方法分析解决问题的能力以及发散思维。

3.效果評价

通过一题多解的研究性教学，学生一起自主讨论、探索，学生的学习兴趣有了提高，师生互动更充分，课堂气氛更加活跃。

探索问题导向的研究型教学模式，不仅仅是要提高教与学的效率，从某种程度上更是培养学生的思维能力，对学生素质能力的锻炼，这才是当前改革热潮追求的最根本的教育目标。在《复变函数》课程中引入基于问题导向的研究型教学理念，通过引导学生深度思考研究，运用数学解决现实问题，旨在通过新教育模式将课堂教学流程再造，着力培养学生的创新精神和研究解决问题的能力。

基金项目：山东科技大学济南校区优秀教学团队（JNJXTD201713）

参考文献：

[1]孙会霞，陈红如.以问题为导向的大学数学课程教学模式研究与探讨[J].河南教育：高教版（中），2014.

[2]刘晓妍，王言英.“问题驱动”在高等数学教学中的应用[J].河南教育学院学报：自然科学版，2014.

[3]王芬玲，樊明智.研究性教学在复变函数课堂中的应用[J]. 科技信息，2011，000（022）：117-117.

[4]华中科技大学数学与统计学院 李红 谢松法.复变函数与积分变换[M].4版.北京：高等教育出版社， 2013.

[5]张晓军，席酉民，赵璐.研究导向型教育[M].北京：机械工业出版社，2017.