渗透守恒思想，发展“能量观”，促进思维提升

◇ 金朝娣 姚 芳 耿 薇

新课程标准提出，能量观是物理学科核心素养要素中物理观念的重要组成部分.能量观的核心内容是：自然界中有多种形式的能量，能量可以从一种形式转化为另一种形式，或者从一个物体转移到另一个物体，在转移和转化过程中，有些能量变化，而总能量保持不变.所以能量是“守恒量”，而守恒量对应的守恒关系是自然界中重要的关系，更是解决物理问题的重要工具.此外，能量涉及的守恒思想也是学生需重点领悟和应用的一种物理学思想方法.纵观近几年的高考、等级考、合格考等重要考试，利用守恒思想解决物理问题是重要的考查方向之一.

运用守恒思想解决实际问题能力的高低，取决于学生对各类守恒定律的理解程度.在针对性复习时，除知悉具体知识考查要点外，还应从物理学科核心素养的角度，分析此类试题的命题立意和考查目标，借助守恒的观点正确高效地分析复杂问题，在促进具体知识提升的同时，逐步渗透守恒思想.

下面笔者以京师AI联考中一道与“守恒”相关的物理计算题为例，从学科核心素养的视角出发，挖掘原题中的考查目标、思维障碍点和答题技巧，从逐点击破到归纳整合，帮助同学们在形成清晰知识脉络的同时，逐步学会以能量的观点和守恒的思想来分析复杂问题，从而在备考中实现高效复习.

原题呈现：如图1所示，光滑水平地面的左端固定一光滑的半径为R的圆形轨道BC，水平地面与圆形轨道相切于C点，水平地面上有一轻质弹簧，其右端连接一质量为3m的小球Q，小球处于静止状态，现有一质量为m的小球P从B点正上方距B为R的高处由静止释放，两小球均可视为质点，重力加速度为g.

图1

(1)求在小球P压缩弹簧的过程中，弹簧储存的最大弹性势能Ep；

(2)若小球P从B点上方高H处由静止释放，第一次经过C点后，立即将BC换成半径也为R的固定光滑圆弧轨道CBD，与水平面仍相切于C点，为使小球P经弹簧反弹后恰能通过轨道CBD的最高点，求H.

1 核心素养视域下试题指向能量观的考查目标

本题主要涉及的核心素养要素为：物理观念和科学思维，其中物理观念是物理学科核心素养的重要组成部分，具体包括物质观、运动观、能量观、相互作用观.

1)以“多过程”为切入点，考查学生对于能量概念的理解

此题需要学生清晰、系统地理解试题涉及的动量、动能、势能和机械能等物理概念，灵活利用动量守恒定律和机械能守恒定律解决多过程、综合性的问题，在解决问题过程中形成能量观.能量概念之所以重要，是因为它是个“守恒量”，而这个“守恒量”又包含了动能、势能和机械能等各种能量概念，这些能量概念往往是学生容易混淆的内容.

2)渗透守恒思想，促进科学思维的发展

建构模型，熟练利用物理规律和科学方法解决具体的物理问题，是发展科学思维的重要途径.此题需要根据情境确定运动模型，同时借助牛顿第二定律、动量守恒定律和机械能守恒定律来解决多过程问题，从而促进科学思维的发展.

该题涉及的能量观的具体知识点和关键能力的培养如表1所示.

表1 指向学科核心素养的考查目标

2 思维障碍点分析及对策

1)从多过程情境中抽取物理模型的能力欠缺，制约了科学推理

遇到多过程情境时，需要挖掘情境中的隐含条件，把整个过程进行分解，抽象出典型的物理模型，并对具体的模型进行研究，最后利用核心概念和规律进行科学推理，这是培养科学思维的重要途径之一.

本题第(1)问求在小球P压缩弹簧的过程中，弹簧储存的最大弹性势能.如果在解题时没有分解过程并建立运动模型的意识，对于此问会陷入毫无头绪或生搬硬套公式的错误思路.如果以小球P为研究对象，通过受力分析，不难发现，小球P从B点正上方距B为R的高处由静止释放到压缩弹簧的过程共涉及4个过程，分别对应4个物理运动模型.同理可得，第(2)问小球P涉及的过程有6个，具体如表2所示.

表2 多过程问题中的物理量变化梳理(以小球P为研究对象)

通过梳理过程，知道了哪些物理量变化，哪些不变，就能很快明确各类能量转移转化的来源和去向，为解题奠定了基础，同时初步判定动量守恒定律和机械能守恒定律的条件.

2)对各类能量概念和守恒定律认识“似是而非”，解决问题时“生搬硬套”

很多同学将物理公式或守恒定律熟记于心，却忽略了对各类能量概念、功的概念、做功的定义以及守恒规律的深入理解，导致应用时混淆不清，“似是而非”.

例如，此题涉及动能、弹性势能、重力势能和机械能的概念，涉及动量守恒定律和机械能守恒定律，根据笔者经验，学生对于动能、弹性势能和重力势能的概念较为清晰，但对于机械能容易出错，最典型的错误是很多学生将电场中的电势能误认为是机械能.另外，很多学生容易将动量定理和动量守恒定律混淆，解决问题时“生搬硬套”.

3)各类功能关系混淆不清，甚至“张冠李戴”

能量转化一定伴随着做功，绝大部分同学清楚弹力做功、重力做功分别引起弹性势能和重力势能的变化，但一些同学对于合外力做功，或除了重力和弹力以外的力做功会引起什么能量变化并不清楚.在解决此题时，容易将机械能守恒定律、动能定理和能量守恒定律“张冠李戴”.

4)科学方法的缺乏制约解题效率

此题虽涉及能量观，但属于多过程的综合性问题，解决此类物理问题时，除抽取物理模型、深入理解基本概念和规律以及明确规律的应用条件外，还要选择合适的科学方法来提高解题效率.比如，此题第(1)问小球P与弹簧接触直到弹簧被压缩到最短、小球P与Q共速，这一过程可以类比完全非弹性碰撞，再如，第(2)问小球P与弹簧接触直到弹簧恢复原长、小球P再次离开弹簧这一过程可以类比弹性碰撞.

如果考生能熟练应用类比的方法，结合正确分解过程，构建准确的物理模型，清晰各类能量概念和守恒定律的应用条件，此题就会迎刃而解.具体解题过程如下：

(1)小球P从A点运动到C点的过程中，由机械能守恒定律有

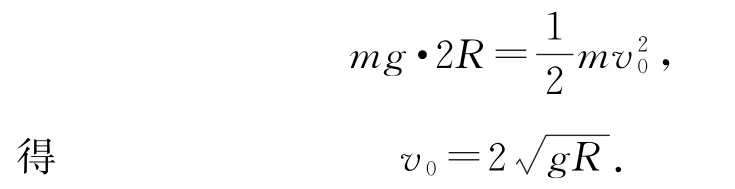
当P、Q两球速度相等时，弹簧具有的弹性势能最大，设共同速度为v，由动量守恒定律有

由能量守恒定律得

(2)设小球从P点上方高为H处释放，到达水平面的速度为.由机械能守恒定律有mg(H＋R)＝弹簧被压缩后再次恢复原长时设小球P和Q的速度大小分别为v1和v2，则根据动量守恒定律有＝－mv1＋Mv2.根据机械能守恒定律有

若小球恰能通过轨道CBD的最高点，由牛顿第二定律有.由机械能守恒定律有

由以上关系得H＝9R.

3 此题对涉及能量观综合类问题复习的导向性

1)重视各种物理概念的理解、功能关系的梳理，促进能量观的进一步发展

物理概念和规律是考生形成物理观念的有机组成部分，更是从碎片知识到概念体系，从具体方法到科学思维过程中不可或缺的一步.而对能量概念的清晰认识和深刻理解是追寻“守恒量”的基础，既能知晓做“功”和“能量”的区别，又能将“功”和“能量”联系起来，梳理出正确的功能关系，明确能量转化的来源和去向，是解决能量问题的关键，也是促进能量观进一步发展的必备要素.

2)寻找多过程中各种能量的“变”与“不变”，渗透守恒思想

遇到综合性强，特别是多过程性问题时，要学会应用分解的思想，将大过程细化成小过程进行分析.不妨采用列表的形式，梳理各过程中哪些能量是变化的，哪些是不变的，并反思为什么变化，为什么不变，思考因果关系的同时，逐步渗透守恒思想.最后将小过程中的核心问题结合成一个整体进行综合分析和认识，在发展能量观的同时，科学思维也将得到提升.

3)应熟悉科学思想和方法，促进整合归纳能力的提升

中学物理教学涉及很多科学思想和方法，例如类比思想、逆向思维、等效思想、割补法等，在学习过程中应善于总结和应用，促进解题思维高度和维度的提升，养成全面看待问题的习惯和思维品质.

4 总结与反思

涉及能量观的综合类物理问题是各类考试的重要考查方向，解决此类问题时，应围绕核心概念和规律，借助模型构建并熟悉能量转化的来源和去向.在解决问题过程中，多角度分析问题，不仅能提升具体知识的理解，还能促进科学思维的发展.