基于移动边缘计算的时延能耗最小化安全传输

（西安交通大学信息与通信工程学院，陕西 西安 710049）

1 引言

随着5G 万物互联时代的到来，网络中移动终端数量激增且设备异构程度显著增加。同时，随着虚拟现实、智能驾驶、视频监控、在线游戏等计算任务繁重或实时性要求高的业务的兴起，无线资源和移动终端面临巨大挑战。相比于网络核心设备，移动终端计算能力有限，存储有限，且通常为电池供电。在上述资源严重受限的条件下，单一依靠终端设备完成计算密集型任务将面临不小的挑战。云计算[1]将移动终端的计算任务卸载给云服务器，从而大大减轻终端设备压力。然而，对于物联网等大量设备接入场景，海量数据涌入云计算中心将会造成核心网拥塞，降低服务体验。因此，作为另一种计算卸载方案，移动边缘计算（MEC,mobile edge computing）[2-4]近年来受到广泛关注。MEC 将计算资源从远端云下拉到无线接入网络侧，通过给基站等网络边缘节点配备计算、处理、存储能力，就近为移动终端提供计算服务。相比于云端，边缘节点距离终端设备更近，可以更高效地在本地完成对数据的处理。

当前及下一代移动通信网络对计算、存储资源的迫切需求推动了有关MEC 研究的快速发展。目前国内外已有一系列针对MEC 协助移动终端进行计算卸载的研究，按照卸载方式可以分为全部卸载[5-7]和部分卸载[8-10]。文献[5]研究单用户衰落信道下本地计算和边缘计算的选择以使能耗最小化，并对本地模式下中央处理器（CPU,central processing unit）频率，以及边缘计算模式下数据传输速率分别进行优化。文献[6]研究能量收割多用户场景下本地计算和边缘计算选择以最大化用户计算速率之和。文献[7]提出了MEC 中继网络端到端时延最小化的文件压缩与解压方案，最优方案呈现本地处理或MEC 服务器处理的二元性结构。与全部卸载不同，部分卸载允许计算任务分块在本地和边缘节点同时进行。文献[8-9]利用随机优化理论解决动态计算卸载问题，取得了能耗和时延的折中。文献[10]利用博弈论思想提出一种基于终端直通通信、边缘计算、云计算三者结合的分层任务卸载方案。

虽然关于MEC 卸载的研究已取得大量成果，但MEC卸载面临的一大重要问题是隐私泄露问题，需要在提供计算服务的同时保障用户数据的隐私性。隐私保障主要有2 个层面：数据共享的隐私性，数据传输的隐私性。前者关注于共享设备的身份认证，后者关注于共享数据的安全传输。本文重点研究计算卸载过程中数据经无线信道传输的安全性问题。由于无线电波的开放性，移动终端通过无线信道传输使边缘节点的数据直接暴露在窃听者的监听之下，边缘节点返回给终端的计算结果也同样面临被窃听的风险。因此，如何保障终端设备与MEC 服务器之间无线传输的安全性，成为一个亟待解决的问题。

无线传输的隐私性保障一直是一个热门话题。有别于传统互联网中采取的单一上层加密[11]方法，无线通信网络具有信道随机多变的特性，这为对抗窃听提供了额外的资源，可以在物理层进行设计以提高通信安全性。此外，在一些分布式无线网络中，不存在中心设备支持密钥分发管理，这为高层加密的普及带来困难。针对这一问题，物理层安全[12]在近年来得到了广泛的关注。通过使用窃听编码[13]结合多天线信号处理、协作通信等技术，物理层安全可以收割合法信道相对于窃听信道的优势，从而实现信息论意义上的绝对安全。国内外已有一些学者针对物理层安全辅助的MEC 安全计算卸载展开研究[14-17]。文献[14]研究窃听者信道信息非完美已知情况下，人工噪声的设计和计算负载的分配，同时引入代价函数刻画移动终端使用MEC 服务器需要支付的费用。文献[15]考虑多用户多载波系统中，当窃听者信道存在估计误差时，计算负载和无线资源的分配问题。对于更一般的场景，即只知道窃听者统计信道信息，文献[16]提出了安全概率约束下的计算卸载方案。此外，文献[17]将安全计算卸载扩展到了无人机通信网络，通过让全双工无人机和空闲地面用户发射人工干扰信号，从而保障计算负载的安全卸载。

然而，上述文献只考虑一个窃听者的情况，且均假设窃听者的位置和信道信息部分已知。此外，上述研究集中于单跳通信，忽视了中继网络中的安全计算卸载问题。因此，与文献[7]相似，本文考虑一个配备MEC 服务器的智能基站作为中继协助移动终端，完成文件压缩、传输、解压的两跳通信系统。针对该系统中的安全计算卸载问题，本文采用空间泊松点过程刻画随机分布窃听者对该系统文件传输带来的信息泄露风险。在此基础上，提出了一种综合考虑安全、时延和能耗的压缩、传输与解压方案。具体地，本文首先推导出文件经两跳传输后的安全传输概率，基于此构建了安全传输概率约束下的时延及能耗最小化问题。为了求解该问题，先将原问题拆分为码本速率设计和计算任务分配2个子问题，再通过一维搜索叠加线性规划得到原问题的最优传输方案，并通过仿真分析了系统参数对方案性能的影响。本文的主要贡献可以归纳如下。

1)针对配备MEC 服务器的中继系统，研究了综合考虑时延和能耗的安全传输与计算任务分配问题。

2)考虑了网络中位置分布未知的窃听者，采用随机几何理论刻画了中继系统在面对这些窃听者时的安全传输概率。

3)基于安全传输概率约束，构建了时延及能耗最小化问题，并通过一维搜索和线性规划得到了最优的码本速率设计和计算任务分配方案。

2 系统模型

2.1 系统描述

智能基站协助的两跳文件传输系统如图1 所示，网络中所有节点均配备单天线。发送端需要传输一个未经压缩的Mbit 文件给接收端，如监控设备录制的画面，智能基站作为中继协助完成文件由发送端到接收端的传输，此处的智能基站不仅具有传统意义上的转发功能，还可以对文件进行压缩和解压处理。除上述3 个合法节点外，网络中还存在若干位置未知、信道状态信息未知的窃听者，他们试图窃听该中继系统所传输的文件，因此对文件的隐私性构成威胁。假设文件可以在发送端、基站、接收端进行压缩和解压处理，压缩率为β∈(0,1]，并假设文件可分割1虽然在这里首先假设文件可分割，但随后的结论1 证明最优计算任务分配方案基于对文件整体的处理，因此所提方案也适用于文件不可分割的情况。，从而对文件的处理可以分块进行[7,16]。为了对抗窃听者，发送端和基站采用窃听编码[13]对处理后的文件进行编码，然后再经由无线信道传输。为了提升两跳传输的安全性，基站采用与发送端不同的码本进行窃听编码，这样在每跳传输安全的前提下，即使窃听者将两跳信息合并也无法获得有用信息[18-19]，从而每跳的传输安全性可以单独考虑。

图1 智能基站的两跳文件传输系统

如图1 所示，假设发送端对Mbit 原始文件中的x∈[0,M]bit 进行压缩，则第一跳（发送端到基站）传输的总比特数为L1=βx+M−x。基站成功解码来自发送端的数据后，进一步对文件进行压缩或解压。值得注意的是，若基站都进行这2 种操作，最终可以等效为单纯的压缩或解压处理，而2 种操作都进行只会造成时延和能耗的增加。因此，基站只需从压缩和解压操作中二选一。假设基站选择对文件未压缩内容中的y1∈[0,M−x]进行压缩，则第二跳（基站到接收端）传输的总比特数为L2=βx+βy1+M−x−y1。相反，若基站选择对文件已压缩内容中的y2∈[0,βx]bit 进行解压，则第二跳传输的总比特数为。

本文考虑准静态信道模型，即信道状态在两跳传输过程中保持不变。发送端到基站和基站到接收端的信道称作合法信道，分别记作，其中，h1和h2对应于小尺度衰落，假设其服从均值为0、方差为1 的复高斯分布；g1和g2刻画了路径损耗。本文采用文献[20]中的路径损耗模型，该模型具体如式(1)所示。

基于式(1)所给出的路径损耗模型，g1和g2可以表示为

其中，α0=10−3.018，η=2.6，d1和d2分别代表发送端与基站和基站与接收端的距离。

2.2 安全传输概率

由于基站采用与发送端不同的码本进行窃听编码，根据文献[18]，图1 所示中继网络的端到端安全传输概率为

其中，Psec,i代表第i跳（i=1,2）安全传输的概率，取决于第i跳窃听编码所使用的码字速率Rt,i和私密信息速率Rs,i(Rt,i＞Rs,i)。由文献[21]可知

其中，Ce,i是窃听信道的信道容量，Rt,i−Rs,i表示为了对抗窃听引入的冗余速率。当窃听者的信道容量小于该冗余速率时，所传私密信息对窃听者完全保密；反之，若窃听者的信道容量大于该冗余速率，则信息泄露发生。

不同于已有工作假设知道单个窃听者的部分信道信息[14-17]，本文考虑更一般的场景，即网络中存在多个窃听者，且窃听者的位置和信道信息完全未知。对于窃听者在网络中随机分布的场景，可采用均匀泊松点过程（HPPP,homogenous Poisson point process）建模窃听者的数量和空间分布[22-27]，从而刻画该场景下私密信息泄露风险。假设窃听者服从密度为λE的均匀泊松点过程，则任意封闭区域S 内窃听者的数量服从式(5)所示的泊松分布。

其中，Φ(S)表示落入区域S 内窃听者的集合，μ=λEv(S)为式(5)中泊松分布的期望，v(S)为区域S 的面积。根据HPPP 的性质，当已知Φ(S)=n时，这n个点在区域S 内服从空间上的均匀分布。此外，假设每一跳的窃听者服从独立同参数λE的泊松点过程，该假设下的安全传输概率是窃听者在两跳传输过程中保持不变时安全传输概率的下界[24]。

下面计算每一跳的安全传输概率。发送端和基站的发射功率分别为PT和PB。假设第一跳传输时，网络中随机分布的窃听者构成集合ΦE,1=(Ej,j=1,2,…}。与式(2)所示合法信道模型类似，发送端与窃听者Ej之间的信道为，其中，表示发送端与Ej之间的距离，表示小尺度瑞利衰落信道。对于每个窃听者Ej，由香农定理可得其单位带宽的信道容量为

其中，N0为加性高斯白噪声的功率，则式(4)中的安全传输概率[23-24]为

步骤(a)由均匀泊松点过程的生成函数[22]得到，步骤(b)由文献[28]得到。

假设第二跳传输时网络中随机分布的窃听者构成集合ΦE,2={Ej,j=1,2,…} 。由式(6)和式(7)可知，第二跳安全传输概率为

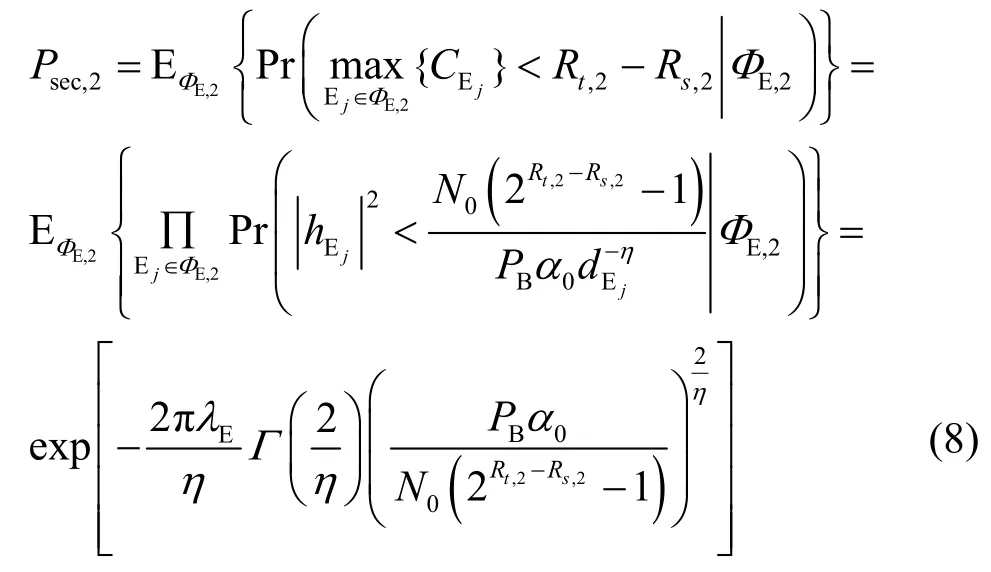
将式(7)和式(8)代入式(3)，可得最终中继网络的端到端安全传输概率。

2.3 时延

本文考虑传输时延和计算时延。因此，图1 所示通信系统的总时延包括5 个部分：发送端计算时延tT、第一跳传输时延t1、基站MEC 服务器计算时延tM、第二跳传输时延t2和接收端计算时延tR。下面分别给出这5 种时延的具体表达式。

假设发送端和接收端CPU 频率为fu，基站所配置MEC 服务器的CPU 频率为fM，每执行1 bit压缩操作需要CPU 周期lc次，每执行1 bit 解压操作需要CPU 周期ld次。由之前的系统描述可知，发送端对原始文件中的xbit 进行压缩操作，则发送端计算时延为

已知第一跳的私密信息速率为Rs,1，系统带宽为B，则第一跳传输时延为

基站处MEC 的计算时延及随后第二跳传输时延和接收端计算时延取决于基站进行压缩还是解压处理，具体如下。

情况1基站选择对文件未压缩内容中的y1bit进行压缩，则MEC 的计算时延为

已知第二跳私密信息速率为Rs,2，系统带宽为B，则第二跳传输时延为

此时，在接收端有(βx+βy1) bit 文件处于压缩状态，则接收端进行解压处理的计算时延为

由上述分析可知，情况1 下系统总时延为

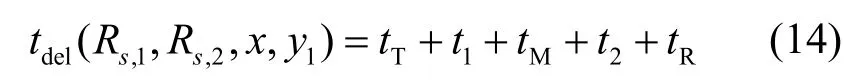
可以看出，总时延是私密信息速率(Rs,1,Rs,2)及计算任务分配方案(x,y1)的函数。

情况2基站选择对文件已压缩内容中的y2bit进行解压，则MEC 的计算时延为

已知第二跳私密信息速率为Rs,2，系统带宽为B，则第二跳传输时延为

在接收端，仍有(βx−y2)bit 文件需要解压，则接收端解压耗时为

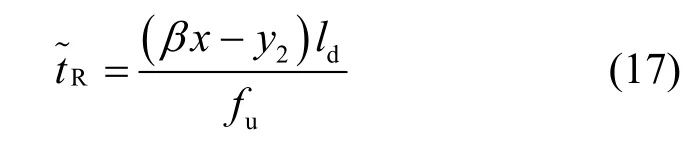
由上述分析可知，情况2 下系统总时延为

可以看出，总时延是私密信息速率(Rs,1,Rs,2)及计算任务分配方案(x,y2)的函数。

2.4 能耗

本文考虑传输能耗和计算能耗[10,14]，则总能耗包括以下5 个部分：发送端计算能耗ET，第一跳传输能耗E1，MEC 服务器计算能耗EM，第二跳传输能耗E2和接收端计算能耗ER。

已知发送端的发射功率为PT，则第一跳的传输能耗为

其中，t1由式(10)给出。根据文献[14]，频率为f的CPU 的功耗可以近似为κf3，功耗因子κ由CPU的结构决定。因此，发送端的计算能耗为

与时延类似，基站处MEC 的计算能耗以及随后第二跳传输能耗和接收端计算能耗取决于基站进行压缩还是解压，具体如下。

情况3基站选择对文件未压缩内容中的y1bit进行压缩，则MEC 的计算能耗为

已知基站发射功率为PB，则第二跳传输能耗为

其中，t2由式(12)给出。由式(13)可知，接收端解压能耗为

新时代，昆楚大铁路开通运营，大理、楚雄与文山、红河4个民族自治州齐刷刷迈入高铁时代；随着广深港高铁开通，今年9月23日高铁牵手春城昆明与东方之珠香港……

情况3 下系统总能耗为

情况4基站选择对文件已压缩内容中的y2bit进行解压，则MEC 的计算能耗为

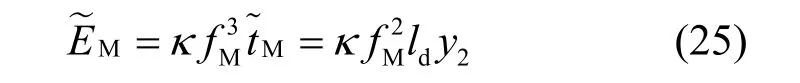
相应地，第二跳的传输能耗为

情况4 下系统总能耗为

可以看到，系统的端到端时延及能耗取决于计算任务分配和每跳码本中的私密信息速率。显然，私密信息速率越高，系统时延越小从而能耗也越小。然而，由式(4)可以看出，高私密信息速率会降低传输的安全性，这是因为在给定码字速率Rt,i条件下，用于对抗窃听的冗余速率会随着私密信息速率提高而下降，从而降低安全传输概率。下一节将讨论给定端到端安全传输概率约束下的最优码本速率设计和计算任务分配。

3 安全概率约束下的时延能耗最小化传输

本节讨论端到端安全传输概率约束下的时延与能耗最小化传输方案。首先，基于第2 节中的分析构建了时延能耗最小化问题，接下来，将该问题拆分为码本速率设计和计算任务分配2 个子问题。码本速率设计采用一维搜索求解，计算任务分配为线性规划问题可通过凸优化工具包求解，算法总流程在本节的最后给出。

3.1 问题构建

考虑时延和能耗的最小化，这是一个典型的多目标优化问题。通过引入非负加权因子，可以将多目标优化转换成单目标优化。此外，由第2 节的分析可知，系统时延和能耗取决于基站的决策。基站有压缩和解压2 种决策，因此可以构造2 个优化问题，每个问题对应于基站的一种决策，最终选取目标函数值最小的方案作为整个问题的最优解。

其中，θ1∈[0,1]和θ2∈[0,1]分别为时延和能耗的加权因子。式(29)中第一个约束条件保证端到端传输的安全性；第二个约束条件是因为原始文件只有Mbit；第三个约束条件是因为在发送端已压缩xbit 的基础上，只剩余(M−x)bit 文件未被压缩。

对于基站选择解压y2bit 的情况，满足安全传输概率约束的时延能耗最小化问题为

其中，θ1和θ2是与式(29)中相同的时延和能耗的加权因子。式(30)中最后一个约束条件是因为在发送端已压缩xbit 的基础上，只有βxbit 文件处于压缩状态，因此基站最多只能解压βxbit 文件。

优化问题Q1和Q2分别求得各自的最优解后，从二者中选择目标函数值最小的解作为整个问题的最优解，即时延能耗最小化意义上的最优传输方案。观察式(29)和式(30)，Q1和Q2的求解均涉及对码本速率(Rt,1,Rs,1,Rt,2,Rs,2)及对计算任务分配方案(x,y1)或(x,y2)的优化，且二者相互耦合，使问题的求解非常困难。然而，当码本速率给定时，关于计算任务分配的求解相对简单。因此，将Q1和Q2分解为码本速率设计和压缩与解压方案设计两部分，对这两部分分别求解再耦合，最终可以得到原问题的最优解。

3.2 码本速率设计

由于优化问题Q1与Q2具有相似性，下面的求解以Q1为例。问题Q1的目标函数是Rs,1和Rs,2的单调递减函数。因此，为了使目标函数最小，Rs,1和Rs,2应尽可能大，但同时需满足式(29)中对最低安全传输概率的约束。回顾式(7)和式(8)，Psec,1和Psec,2分别随着Rs,1和Rs,2的增加而减小，因此最大的Rs,1和Rs,2在Psec,1Psec,2=ε0处取得。此外，给定Psec,1和Psec,2时，Rs,1和Rs,2随着Rt,1和Rt,2的增加而增加。因此，为了最大化私密信息速率，应首先最大化码字速率。

根据文献[21]，为了使目的接收机能正确解码，Rt,1和Rt,2最大不超过目的接收机的信道容量。假设发送端和接收端知道合法信道的瞬时信道信息，即，则由式(2)和香农定理可得两跳的码字速率分别为

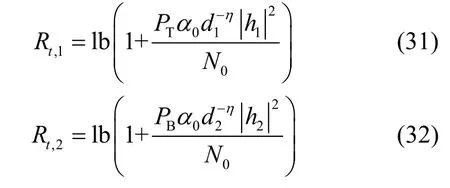
将式(31)和式(32)分别代入式(7)和式(8)，可得每跳安全传输概率的表达式为

如前所述，最优Rs,1和Rs,2在Psec,1Psec,2=ε0处取得。将式(33)和式(34)代入Psec,1Psec,2=ε0，可以发现这是一个二元等式，有多个解，而不同的私密信息速率会导致不同的计算任务分配方案，从而影响优化问题Q1的目标函数值。因此，令Psec,1=ε1，则，通过对ε1进行一维搜索来遍历所有可能取值。给定Psec,1=ε1，由式(33)可得，第一跳私密信息速率为

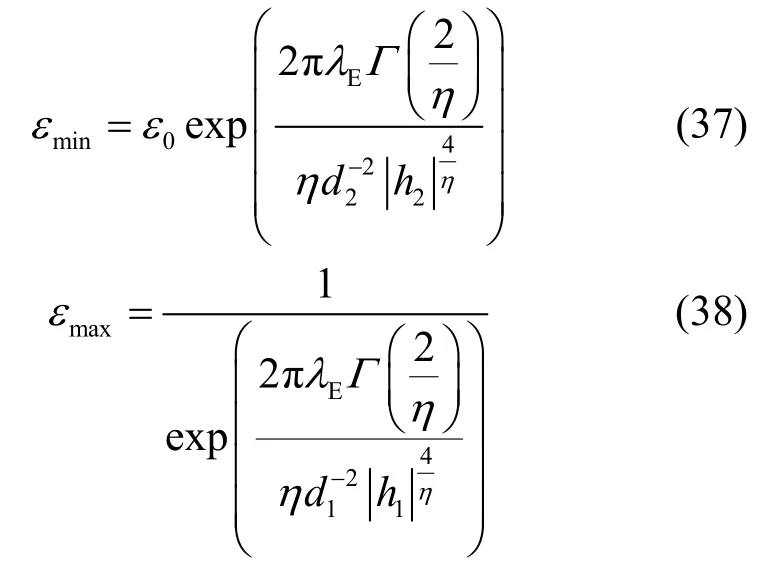
由上述分析可知，对于任意给定的ε1∈[εmin,εmax]，码字速率Rt,1和Rt,2由式(31)和式(32)给出，而私密信息速率Rs,1和Rs,2由式(35)和式(36)确定。当εmin＞εmax时，合法信道的当前信道质量不能满足安全传输需求，传输暂停。对于问题Q2，式(31)～式(38)同样适用，因为码本速率设计只与安全传输概率约束有关，而与计算任务分配方案无关。相反，计算任务分配与码本速率设计有关。

3.3 压缩与解压方案设计

当给定码本速率(Rt,1,Rs,1,Rt,2,Rs,2)后，式(29)和式(30)中的优化问题分别简化为

与优化问题Q1和Q2相比，式(39)和式(40)中没有了安全传输概率约束，这是因为该约束已用于码本速率设计。式(39)和式(40)都是线性规划问题，可以用凸优化工具包CVX[29]求解。进一步地，由于式(39)和式(40)是二元线性规划问题，基于图解法可以得到如下结论。

结论1最优压缩与解压方案属于以下4 种方案中的一种：1)不压缩直接传输；2)发送端对文件整体进行压缩，接收端对文件整体进行解压；3)基站对文件整体进行压缩，接收端对文件整体进行解压；4)发送端对文件整体进行压缩，基站对文件整体进行解压。

证明式(39)和式(40)优化问题的可行域如图2 中阴影区域所示。

图2 优化问题可行域

显然，式(39)和式(40)目标函数的最优值在各自可行域的顶点取得，而二者中最优目标函数值较小的一方所对应的方案为最终的计算任务分配方案。因此，最优压缩与解压方案来自以下4 个顶点：(0,0)、(M,0)、(0,M)、(M,βM)。当最优方案位于点(0,0)时，发送端和基站不需要进行任何操作，文件直接传输，接收端也不需要解压；当最优方案位于点(M,0)时，发送端对Mbit 原始文件整体进行压缩，基站只进行转发，接收端对压缩后的文件进行全部解压；当最优方案位于点(0,M)时，发送端直接发送原始文件，基站对Mbit 原始文件整体进行压缩，接收端再全部解压；当最优方案位于点(M,βM)时，发送端对Mbit 原始文件整体进行压缩，基站再对压缩后的文件进行全部解压，接收端不需要解压。文献[7]中也得到了类似结论，但与文献[7]直接给出几种特定方案不同，本文采用更普适的模型得出上述结论，同时本文也考虑了传输安全和能耗。

证毕。

3.4 算法总流程

通过外层对ε1的一维搜索和内层给定ε1下对计算任务的分配，最终可以得到安全传输概率约束下的时延能耗最小化方案，算法总流程在算法1 中给出，其中，Δε是搜索步长。

算法1安全传输概率约束下的时延能耗最小化方案

4 仿真结果与分析

本节对安全传输概率约束下图1 所示中继系统的性能进行了仿真评估。具体考虑3 种方案，其中，最小化时延与能耗方案对应于θ1=θ2=1，最小化时延方案对应于θ1=1而θ2=0，最小化能耗方案对应于θ1=0而θ2=1。式(39)和式(40)所示优化问题采用凸优化工具包CVX 求解。如无特殊说明，其他仿真参数设置如下：第一跳传输距离d1=20 m，第二跳传输距离d2=30 m，大尺度路径损耗参考式(1)，合法信道小尺度信道增益；发送端发射功率PT=23 dBm，基站发射功率PB=30 dBm，噪声功率为 −174 dBm/Hz，带宽B=10 MHz；移动端CPU 频率fu=20 MHz，MEC 服务器CPU 频率fM=2 GHz，CPU 功耗因子κ=10−28[14]；每执行1 bit 压缩操作需CPU 周期，每执行1 bit解压操作需CPU 周期[7]。

图3 首先验证式(7)和式(8)对安全传输概率推导的正确性。由于二者具有相同的推导过程，图3以验证式(7)为例，其中Rt,1由式(31)确定。在Monte Carlo 仿真中，考虑一个半径为200 m 的圆形小区，发送端位于圆心，窃听者的个数服从式(5)所示的泊松分布，且每次生成的窃听者位置在圆形小区内均匀分布，窃听者的小尺度信道增益服从瑞利分布。由图3 可以看出，理论值与仿真值非常吻合，验证了理论推导的正确性。此外，安全传输概率随着窃听者密度的增大而降低，这是因为信息泄露风险随着窃听者的增多而增大。

图3 Monte Carlo 仿真值与理论值对比

下面考察3 种方案在不同系统参数下的性能。图4 和图5 比较了不同文件大小下3 种方案在时延和能耗上的差异，其中带宽B=10 MHz，压缩率β=0.5，安全概率约束ε0=0.8。通过仿真结果可以看出，随着文件容量M的增大，3 种方案的时延和能耗均增大。这是可以预见的，因为计算任务量和无线信道传输比特数均增大。此外，随着窃听者密度的增大，3 种方案的时延和能耗也增大，这是因为私密信息速率随λE增大而减小，导致每跳传输时间增加，从而在固定发射功率下能耗也增加。最后，对比图4 和图5 可以看到，最小化能耗方案虽然可以实现最低能耗，但大大提升了整个系统的时延，而最小化时延与能耗方案可以对二者进行兼顾。

图6 和图7 比较了不同带宽和压缩率下3 种方案在时延和能耗上的差异，其中文件大小M=100 KB，安全概率约束ε0=0.8，窃听者密度λE=4 ×10−5。对于最小化时延与能耗方案，当带宽小于7 MHz 时，高压缩率（β=0.3）与低压缩率（β=0.6）下的性能有差异，而当带宽大于7 MHz时，不同压缩率下系统性能一样。这说明，当带宽比较小时，图1 所示的两跳传输需要压缩，而当带宽比较大时则不需要压缩。虽然在带宽位于4～7 MHz 时，高压缩率对应时延略高于低压缩率对应时延，但高压缩率大大减小了系统能耗，因此，高压缩率仍有助于目标函数的减小。类似地，对于最小化时延方案，当带宽小于4 MHz 时，传输需要压缩，而当带宽大于4 MHz 时就不需要压缩。对于最小化能耗方案，由于传输能耗远大于计算能耗，出于最小化能耗的目的总是在发送端对文件整体进行压缩，从而减小传输时延以降低传输能耗。因此，高压缩率下的性能总是优于低压缩率，这是因为高压缩率可以大大减小传输文件大小，从而降低时延与能耗。

图4 不同文件大小下3 种方案的时延差异

图5 不同文件大小下3 种方案的能耗差异

安全传输概率对系统性能的影响在图8 和图9 中给出，其中文件大小M=100 KB，带宽B=5 MHz，压缩率β=0.5，窃听者密度λE=1 ×10−5。从仿真结果可以看出，时延和能耗均随着ε0的增大而增大，也就是说较高的安全传输概率需求将带来较长的时延和较高的能耗。这是因为随着ε0的增大，为了满足安全传输概率，需要引入更多的冗余速率，从而导致私密信息速率的减小。在给定总私密文件大小的情况下，每跳私密信息传输速率的下降将导致每跳传输时间的增加，从而在固定发射功率下能耗也增加。对比图4 和图5 可以看出，安全传输概率的提升与窃听者密度的增加对系统性能具有相似的影响。

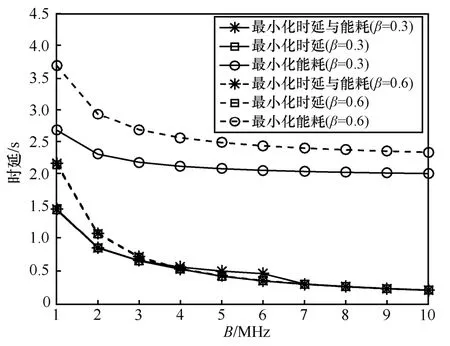
图6 不同带宽下3 种方案的时延差异

图7 不同带宽下3 种方案的能耗差异

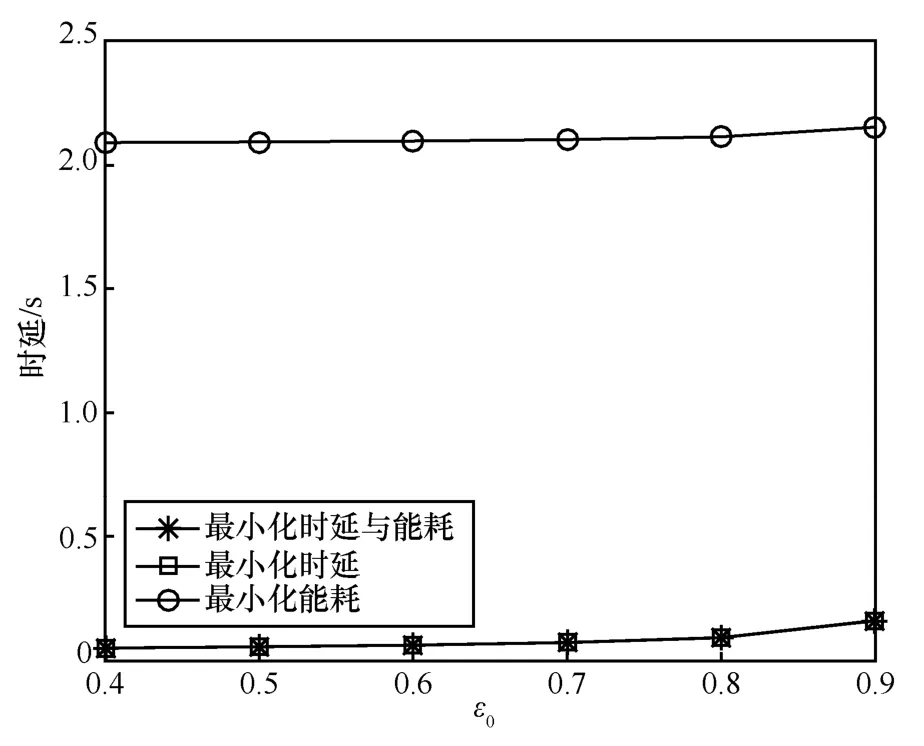
图8 安全传输概率对时延的影响

图9 安全传输概率对能耗的影响

上述仿真结果关注的是系统的时延和能耗，未研究系统参数对计算任务分配方案的影响。表1 给出了最小化时延与能耗方案在给定即每跳安全传输概率相等情况下，最优的压缩与解压方案。其中，文件大小M=500 KB，带宽B=1 MHz，压缩率β=0.5，安全概率约束ε0=0.9，窃听者密度λE=1×10-5。可以看到，最优压缩与解压方案可以归为4 类，这验证了结论1 的正确性。当两跳传输距离均比较短时，两跳的路径损耗均比较小从而私密信息速率高，此时最优方案是直接传输原始文件而不进行压缩。当第一跳路径损耗小而第二跳路径损耗较大时，由于第二跳私密信息速率低，因此需要在基站处对原始文件整体进行压缩从而减小第二跳需要传播的数据量。当第一跳路径损耗大而第二跳路径损耗小时，发送端对文件整体进行压缩以减小第一跳传输的数据量，而基站对压缩文件整体进行解压从而免除接收端解压耗时。最后，当两跳路径损耗都比较严重时，文件一开始就在发送端整体压缩，直到接收端收到文件后再进行解压。

表1 最小化时延与能耗方案在给定下的最优压缩与解压任务分配

表1 最小化时延与能耗方案在给定下的最优压缩与解压任务分配

图10 小尺度信道随机变化时，各传输方案的平均性能

5 结束语

本文研究了智能中继系统中的文件安全传输问题，其中，配备MEC 服务器的智能基站作为中继可以对收到的文件进行压缩和解压处理后再转发。面对网络中随机分布的窃听者，本文研究了在安全传输概率约束下的时延与能耗最小化文件传输问题，通过外层一维搜索和内层线性规划问题求解，得到了最优码本速率设计和计算任务分配方案。仿真结果评估了不同系统参数下该方案的性能，并与单纯的最小化时延以及最小化能耗方案进行了对比。仿真结果表明，给定安全概率约束下可达私密信息速率小的链路在传输前需要进行文件压缩，反之不需要压缩，可直接传输。