无人机无线网络覆盖与切换性能分析

（北京邮电大学网络与交换技术国家重点实验室，北京 100876）

1 引言

无人机网络具有易部署、配置灵活、视距通信概率高等优点，能够在热点区域为现有通信网络提供补充覆盖，或在地面通信设施未覆盖和遭到破坏的极端环境，作为临时基站或空中中继为用户提供服务。因此，无人机通信被认为是未来无线通信的重要组成部分，受到了学术界的广泛关注[1]。其中，无人机的高移动性对无线网络性能的影响是研究的热点和难点。

目前，已有一些文献研究了用户移动性对网络性能的影响。文献[2]利用随机几何分析了单层蜂窝网络用户移动性对切换概率和覆盖概率的影响。文献[3]分析了多层异构网络下用户移动性对网络性能的影响。考虑移动前后相关性，文献[4]分析了用户移动性对联合覆盖概率的影响。然而上述文献在分析切换概率时仅考虑了大尺度路径损耗，忽略了小尺度衰落对网络性能的影响。更进一步地，文献[5]同时考虑了大尺度衰落与小尺度衰落，但没有分析用户高速移动对信道状态信息（CSI,channel state information）估计造成的影响。

用户移动会引发多普勒效应，并导致CSI 估计不准确和过时问题。在高速移动、高频带场景下，过时CSI 对用户性能的影响不容忽视。文献[6]根据过时CSI 对单层超密集网络移动用户的切换概率和覆盖概率进行了分析，但没有涉及对CSI 估计影响更显著的无人机移动场景和更普适的异构网络。

为此，本文针对无人机高速移动场景，考虑无人机高速移动带来的过时CSI 问题，利用随机几何理论对无人机移动用户的切换概率、切换误差概率和覆盖概率进行了理论推导，并分析了关键参数对上述性能指标的影响。

2 系统模型

系统框架如图1 所示。本文考虑双层异构网络，假设层1 和层2 的基站分别配置M1和M2根天线，发射功率分别为P1和P2，每个无人机移动用户配置单天线。基于随机几何理论，假设两层基站与无人机均服从独立的泊松点过程Φ1、Φ2与Φu，密度分别为λ1、λ2与λu。

图1 系统框架

无人机距地面高度为l，并采用随机游走模型对无人机的运动建模[7]，具体表示为无人机在单位时间内以速度v沿任意方向θ运动。为保证无人机的服务质量，无人机接入能提供最大参考信号接收功率的基站，并选择能提供最高信道增益的天线为其服务。此外，接入后的无人机将切换到能提供最大参考信号接收功率的基站。

本文同时考虑大尺度衰落和小尺度衰落。特别地，通过概率视距和非视距信道模型来表征无人机与地面基站间的空对地信道。视距与非视距的概率与环境参数有关[8]，具体地，高度为l且到基站水平距离为r的用户视距概率可表示为

其中，a和b表示与环境有关的常数，r表示无人机到基站的水平距离，表示无人机到地面基站的仰角。由此可知，视距概率随无人机高度l增大而增高，随无人机到地面基站水平距离r增大而降低。根据视距概率表达式，非视距概率可表示为PNL(r)=1−PL(r,l)。为了简化分析，本文将视距概率表达式近似为[9]

其中，βl表示由无人机高度l确定的可调值。由路径损耗造成的大尺度衰落可表示为L=d(t)−α，其中，d(t)表示t时刻无人机到服务基站的距离，α表示信道的路径损耗指数。将视距信道与非视距信道的路径损耗指数分别表示为αL和αNL，且2＜αL＜αNL。同时，假设小尺度衰落为瑞利衰落[10]，即h(t)～CN(0,1)。由于无人机更易与地面基站建立视距信道，已有研究（如文献[13-14]）将空−地信道的小尺度衰落建模为莱斯信道。本文为了便于分析，将空−地信道的小尺度衰落建模为瑞利信道，而将视距和非视距影响整合到大尺度衰落的模型中，类似假设在无人机网络性能分析工作中已被广泛采用，如文献[10-12]。同时，文献[15-16]表明，多径衰落是影响网络性能的次要因素，不会影响本文的主要结论。本文考虑干扰限制的通信环境，即忽略噪声的影响。典型无人机处接收的信干比（SIR,signal to interference ratio）可表示为

其中，x∈{1,2}分别表示无人机接入层1 和层2，y∈{L,NL}分别表示视距与非视距情况。当服务基站在层1 或层2 时，Px=P1或Px=P2；当无人机与基站间信道为视距或非视距时，αy=αL或αy=αNL。典型的无人机受到的干扰可表示为,Φ=Φ1∪Φ2，b0为服务基站。

3 性能分析

由于无人机从基站处得到的反馈CSI 是有时延的，需要根据h(t)计算过时CSI 影响下的小尺度衰落，本文利用Jake 散射模型进行建模[6]，则的概率分布函数（PDF,probability density function）可表示为

其中，M为基站天线数；，ρ=，J0(·)为第一类0 阶贝塞尔方程，τd为时延，为多普勒频率，f为当前使用频率，c为电磁波传播速率，v为无人机移动速度，ω为无人机运动方向与入射波的夹角。

3.1 切换概率

为了分析切换概率和切换误差概率，首先需推导概率视距/非视距信道以及准确CSI 和过时CSI下的修正泊松点过程密度。根据文献[6]可以得到考虑CSI 的修正泊松点过程密度为

其中，λ0为原始泊松点过程密度，H 为小尺度衰落。此外，考虑概率视距和非视距信道影响，y信道的x层基站修正泊松点过程密度为

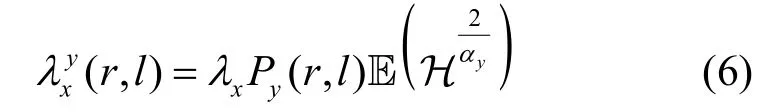
由式(6)可得，修正泊松点过程密度与信道小尺度衰落以及视距和非视距概率有关。当接收到准确CSI 时，H=h(t)～exp (1)，此时；当接收到过时CSI 时，，此时可表示为

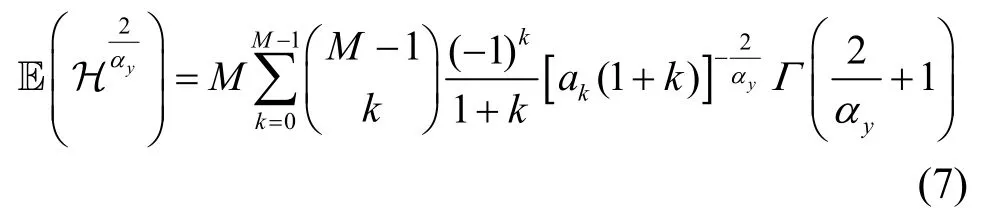
其中，Γ(·)为伽马函数。

根据上述准确CSI 和过时CSI 影响下的修正基站密度，分别推导切换概率与切换误差概率。

定理1当接收到过时CSI 时，典型无人机的平均切换概率可表示为

其中，i和j分别表示典型无人机接入i层基站且处于j信道，表示过时CSI下处于该状态的概率，表示过时CSI 下处于该状态的切换概率。

证明当接收到过时CSI 时，利用泊松点过程的零概率理论，可得到典型无人机接入x层基站且处于y信道下的切换概率为

切换几何面积说明如图2 所示。无人机以高度l、速度v沿θ方向移动，其中，r表示无人机移动前与服务基站的水平距离，与R分别表示过时CSI 下与精准CSI 下修正的无人机移动后与服务基站的水平距离。分别表示以和R为半径，且去除原服务基站以r为半径后的加权面积，表征存在切换基站的面积。由此，根据几何方法，区域面积可表示为

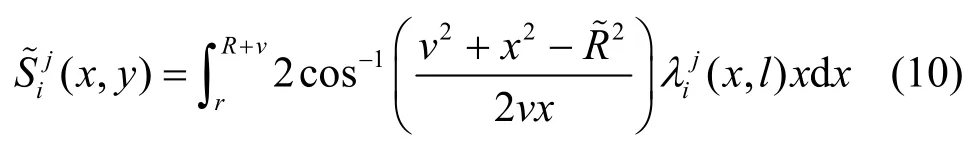
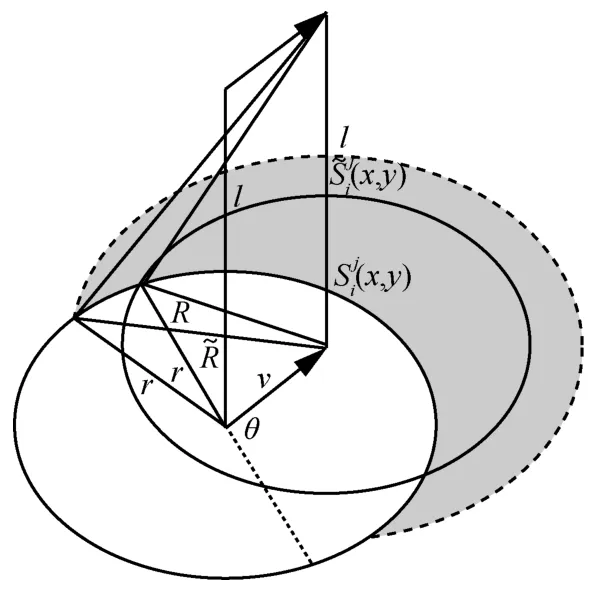
图2 切换几何面积说明

为进一步计算式(9)中的积分，需分别求解θ、、r的PDF，由于无人机建模为随机游走运动模型，运动方向θ服从均匀分布，它的PDF 可表示为。同时，的PDF 可由式(4)得到。这里，假设无人机接入能提供最大参考信号接收功率的基站，则当典型无人机接入x层基站且处于y信道时，用户与基站间距r的条件概率密度函数（CPDF,conditional probability density function）可表示为

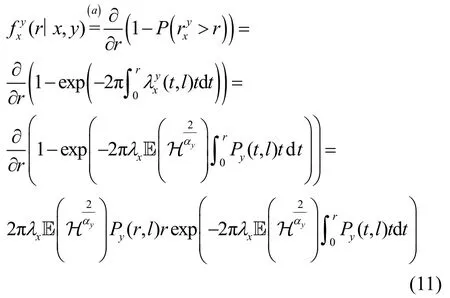
其中，(a)表示对存在处于y信道的x层基站与典型无人机间距离小于r的概率求导，可由式(7)求得。考虑典型无人机接入x层基站且处于y信道的概率，可得到用户与基站间距r的PDF 表达式为

进一步地，通过对用户与基站间距的PDF 求积分，可获得典型无人机接入x层基站且处于y信道下的概率为。

综合以上推导，定理1 得证。

由上述推导可知，典型无人机的平均切换概率主要根据切换加权面积和确定，即与地面基站修正密度、无人机移动速度有关，其中地面基站修正密度取决于地面基站密度、视距和非视距概率以及信道时延。

针对式(12)，通过确定具体所处信道，可获得用户与基站间距r的PDF 的闭式解，在推论1 中表示。

推论1当典型无人机接入x层基站且分别处于视距信道和非视距信道时，用户与基站间距r的PDF 可分别化简为

证明将PL(r,l)=exp(−βlr2)和PNL(r,l)=1−exp(−βlr2)分别代入式(12)中，可证得推论1。

与接收到过时CSI 类似，通过将小尺度衰落由式(4)替换为h(t)～exp(1)，准确CSI 下的平均切换概率在推论2 中表示。

推论2当接收到准确CSI 时，典型无人机的平均切换概率表示为

其中，F(i,j)表示准确CSI 下典型无人机接入基站层i且处于j信道的概率，PH(i,j)表示准确CSI 下典型无人机处于该状态时的切换概率。

证明将中的由式(7)替换为，可获得F(i,j)表达式。类似于式(9)，典型无人机接入x层基站且处于y信道下的切换概率为

综合以上推导，推论2 得证。

进一步地，切换误差概率定义为根据准确CSI和过时CSI 产生不同切换判决的概率，具体包括相比于准确CSI，过时CSI 下切换失败以及误切换的概率和。因此，平均切换误差概率可在推论3 中获得。

推论3典型无人机的平均切换误差概率可表示为

其中，PHF(x,y)为典型无人机接入x层基站且处于y信道下的切换误差概率，具体表示为

根据式(18)可知，切换误差概率取决于误差加权面积，即与无人机移动速度、基站密度有关。当无人机静止时，过时CSI 和准确CSI 下的基站修正密度相同，切换加权面积为0；随着移动速度提升，过时CSI 下的基站修正密度增大，误差加权面积增大；但是当移动速度非常高时，过时CSI 和准确CSI 下的无人机均将切换，误差加权面积减小。因此，切换误差概率随无人机移动速度提升呈先升高后下降趋势。

3.2 覆盖概率

本节根据过时CSI 下，典型无人机接入基站层i且处于j信道的概率，以及给定的SIR 阈值T，推导典型无人机的平均覆盖概率。

定理2在给定SIR 阈值T下，典型无人机的平均覆盖概率可表示为

证明在给定SIR 阈值T下，典型无人机接入x层基站且处于y信道下的覆盖概率为

其中，步骤(a)是由瑞利分布信道的假设得到的。根据过时CSI 反馈计算得到的小尺度衰落的PDF，可以得到小尺度衰落的累积密度函数为

其中，步骤(a)是由gi的独立同分布，以及gi与点过程Φ之间的相互独立获得，步骤(b)则是利用泊松点过程的概率生成函数（PGF,probability generating function）获得，即，且通过将干扰进行分类，可得。

由于干扰信号服从瑞利衰落，则典型无人机接收到g的PDF 与相同，因此式(24)可进一步表示为

综合以上推导，定理2 得证。

由上述推导过程可知，典型无人机的平均覆盖概率由无人机的SIR 和SIR 阈值确定，其中无人机的SIR 与地面基站修正密度、无人机移动速度有关。如果提升无人机移动速度，则会减小有用信号而增大干扰，从而降低无人机的SIR 与覆盖概率，且地面基站密度越高，无人机移动速度变化越明显。

4 数值仿真

本节分别验证切换概率、切换误差概率和覆盖概率理论表达式的准确性，并探究无人机移动性、地面基站密度和飞行高度对上述网络性能的影响。上述双层异构网络仿真在半径为5 km 的圆形区域内，典型无人机放置于圆心处，具体仿真参数如表1所示。

表1 仿真参数

图3 研究了无人机移动速度对过时CSI 和准确CSI 下切换概率及切换误差概率的影响。由图3 可知，切换概率随无人机移动速度提升而增大，这是由于式(10)中切换加权面积随无人机移动速度提升而增大，从而提高了切换概率。值得注意的是，过时CSI 时的无人机切换概率比准确CSI 时更大。原因是针对式(6)中的修正泊松点过程密度，过时CSI相较准确CSI 有高值。此外，切换误差概率随无人机移动速度提升先增大后减小，这是由于无人机从静止到运动，获得的反馈CSI 是有时延的，且切换判定考虑小尺度衰落影响，则根据式(4)和式(7)，过时CSI 下修正泊松点过程密度随无人机移动速度提升而增大，从而根据式(18)切换误差会随移动速度提升而增大，而随着无人机速度增大，过时CSI下修正泊松点过程密度增速减缓，切换误差由切换基站可能出现的实际面积主导，由于高速移动时过时CSI 和准确CSI 下无人机都将进行切换，即切换加权面积随移动速度提升而趋于相同，则切换误差下降。由此可知，在固定地面基站密度下，存在特定的无人机移动速度，使发生错误切换的概率最大，这为无人机网络的部署提供了理论指导。与文献[6]相比，由于采用了概率视距和非视距信道模型，视距概率随着无人机到地面基站水平距离的增大而降低。随着无人机移动速度的增大，切换概率的提升和切换误差概率的降低都更平缓，这是因为视距信道集中于用户附近区域，高速度引起的远距离切换发生概率较文献[6]更低。

图3 过时CSI、准确CSI 下切换概率及切换误差概率随无人机移动速度变化

图4 研究了基站密度对过时CSI 和准确CSI 下切换概率及切换误差概率的影响。与图3 类似，切换概率随地面基站密度增大而增大，且过时CSI 比准确CSI 有更大的切换概率，原因是增大地面基站密度，无人机与服务基站间距离缩短，相同移动速度下，高基站密度更易发生切换。从式(10)也可看出，切换加权面积随基站密度增大而增大，从而提高了切换概率。同时，切换误差概率随基站密度增大呈现先增大后减小的趋势，这是由于相同移动速度下，地面基站密度越高，过时CSI 和准确CSI 间修正泊松点过程密度相差越大，则切换误差随基站密度增大而增大，但当基站密度极高时，增大基站密度，无人机到服务基站距离缩短，可理解为在服务距离不变的情况下增大无人机移动速度，这时过时CSI 和准确CSI 下都将进行切换，则与图3 趋势相似，切换误差下降。同样由于视距信道集中于用户附近区域，因基站密度增大而减小的远距离切换对整体切换概率影响较小，因此相较于文献[6]，随基站密度的增大，切换概率的提升和切换误差概率的降低都更迅速。

图5 研究了不同飞行高度下无人机移动速度对覆盖概率的影响。由图5 可知，覆盖概率随无人机移动速度和飞行高度提升而减小。相较于无人机移动速度，飞行高度对覆盖概率影响更大。同时，随着无人机飞行高度增加，覆盖概率对无人机移动速度变化更加敏感。因此，为保障无人机覆盖概率，无人机移动速度和飞行高度间需要进行权衡折中。相较于文献[6]，本文考虑干扰对无人机覆盖概率的影响，随无人机移动速度增大，用户所受干扰会呈先增大后减小的趋势，因此覆盖概率会先较快速降低而后趋于平缓。

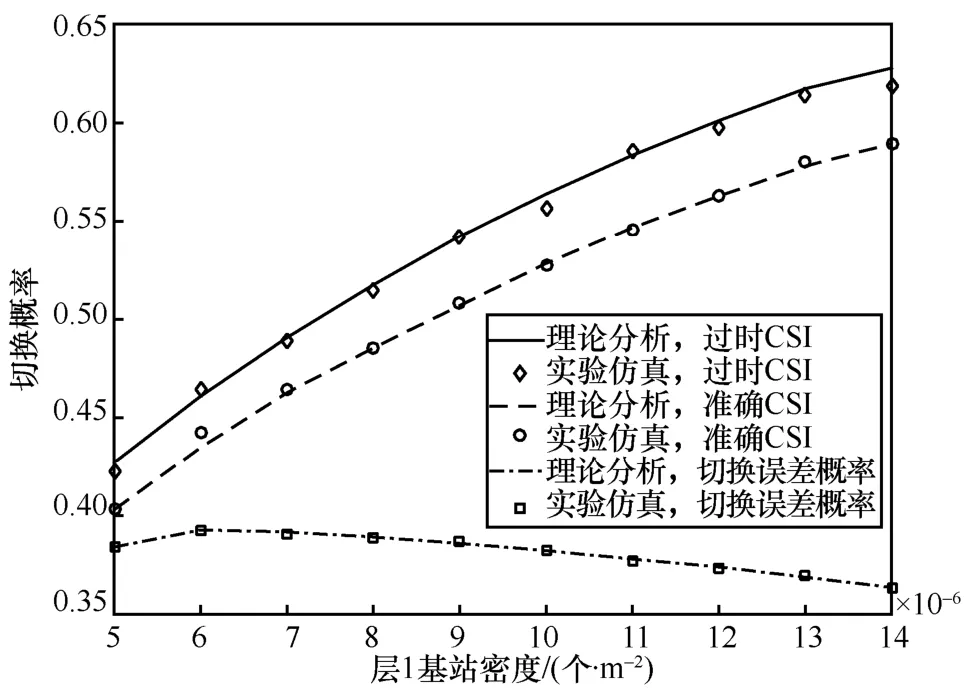
图4 过时CSI、准确CSI 下切换概率与切换误差概率随地面基站密度变化

图5 不同飞行高度下覆盖概率随无人机移动速度变化

5 结束语

本文分析了异构无人机网络的覆盖及切换性能。考虑无人机移动性带来的过时CSI 问题，基于随机几何理论，分别推导了无人机在过时CSI 和准确CSI 下的切换概率、切换误差概率和覆盖概率的解析表达式，探究了无人机移动性、飞行高度和地面基站密度对上述性能的影响。研究表明，过时CSI 会造成切换误差，且随无人机移动速度和基站密度增大呈先增大后减小趋势。此外，相较于无人机移动速度，飞行高度提升对覆盖概率减小影响更加显著。