4t−1 元旋转对称2-弹性函数的构造

杜蛟，刘春红，庞善起

（1.河南师范大学数学与信息科学学院，河南 新乡 453007；2.河南师范大学大数据统计与优化控制河南省工程实验室，河南 新乡 453007；3.河南师范大学计算机与信息工程学院，河南 新乡 453007）

1 引言

文献[2-3]首先研究了具有相关免疫性和高非线性度的旋转对称布尔函数；文献[9-11]研究了平衡的旋转对称布尔函数以及相关免疫旋转对称布尔函数的构造与计数问题；文献[12]研究了相关免疫阶的判别问题；文献[13-17]研究了旋转对称1-弹性函数的若干具体构造方法；文献[18]给出了一个旋转对称弹性函数的二级构造方法，但是该方法依赖于已有的低阶弹性旋转对称函数，构造的函数的变元个数局限性较大；文献[19-20]进一步将旋转对称弹性函数的构造问题从特征为 2 的有限域上推广到特征为奇素数的有限域上。基于以上结果，本文基于轨道交换方法给出了一类具有4t−1 个变元的旋转对称2-弹性函数的构造方法。

2 预备知识

n元布尔函数f0(x)=x1+x2+…+xn不仅是一个n−1阶的弹性函数，还是一个旋转对称布尔函数，记f1(x)=1+x1+x2+…+xn=1+f0(x)，定义

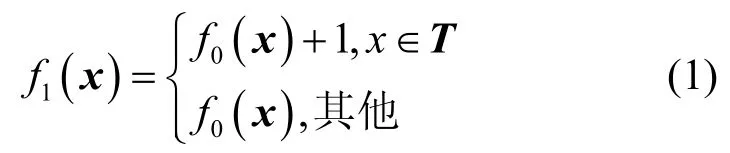
注意到，f1(x)为旋转对称函数的条件是当且仅当集合T是某个旋转对称函数的支撑集[21]，即为若干个旋转对称轨道的并集。向量x=(x1,x2,…,xn)∈的汉明重量为其分量中1 的个数，记为 wt(x)。

定义 1[15]设f(x)∈Bn，记1f={x∈|f(x)=1}，若有|1f|=2n−1，则称f(x)是一个平衡函数，1f是布尔函数f(x)的支撑集或支撑矩阵，集合1f中的向量称为f(x)的支撑向量，1+f(x)的支撑集或支撑矩阵简记为0f。

定义2[22-23]对于有限域F2上的w×n维矩阵A，如果线性空间中的每一个向量都在矩阵A的任意d列中出现相同的次数，则称A是一个正交表 OA(w,n,2,d)。

定义3[23]如果V0和V1都是 OA(2n−1,n,2,d)，满足V0∩V1=∅，且V0∪V1=，则称{V0,V1}为一个强度为d的正交表大集，记为 LOA(2n−1,n,2,d)。

文献[23]给出了相关免疫函数和弹性函数与正交表和正交表大集间的关系，如果一个布尔函数f(x)的支撑矩阵1f是一个正交表OA(w,n,2,d)，则称f(x)是一个d阶相关免疫函数。如果f(x)既是平衡的，又是一个d阶相关免疫函数，则f(x)是一个d-弹性函数，从定义3 可知，d-弹性函数的构造等价于强度为d的正交表大集LOA(2n−1,n,2,d)的构造，本文中的正交均指组合正交性。

下面，考虑循环群Cn=≤l≤n−1}在上的作用，变换定义为

3 旋转对称轨道的性质

为了研究旋转对称 2-弹性函数的构造，下面将在文献[15]的基础上进一步研究旋转对称轨道的性质。假设变元个数n=4t−1，其中t为正整数。

引理1[8]n元旋转对称长轨道的总数为

其中，μ(g)为墨比乌斯函数。

引理2[15]设f(x)为n元旋转对称布尔函数，1f=(c1,c2,…,cn)为f(x)的支撑矩阵，其中ci为1f的第i个列向量，那么存在一个置换矩阵P满足ci+1=Pci,1≤i≤n−1。

引理3[15]设f(x)为n元旋转对称布尔函数，1f=(c1,c2,…,cn)为f(x)的支撑矩阵，ci为1f的第i个列向量，那么f(x)是2 阶相关免疫函数的条件是当且仅当(c1,ck)是一个，其中，。

注：引理3 说明要判断1f是否是强度为2 的正交表，只需判断第1 列与第2～k列分别正交即可，这个结果大大简化了1f是否是强度为2 的正交表的判断过程。

定理1设ROx是n维向量在循环群的作用下生成的一个旋转对称长轨道，则矩阵ROx的任意2 列中，数对01 和10 出现的次数一定相等。

证明由引理2 可知，适当排列ROx的行向量，则ROx可以表示为

其中，di和dj分别是ROx的第i列和第j列，1≤i＜j≤n。下面，考虑di和dj这2 列中数对01和10 出现的次数。根据引理2，dj可以看作由di循环移位得到的，它们的分量中0 的个数和1 的个数分别相等，即如果列向量di的汉明重量wt(di)=w，则wt(dj)=w，其中，1≤i＜j≤n。不妨设由di和dj这2 个列向量构成的n×2矩阵为

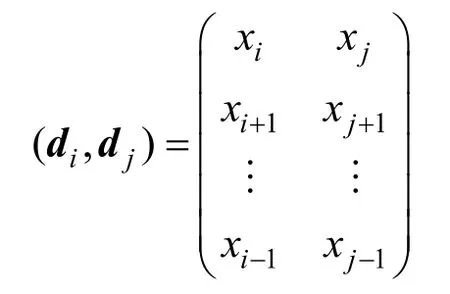
该矩阵行向量构成的n个数对中00、01、10、11 出现的次数分别为N00、N01、N10、N11，则有式(2)所示的方程组成立。

由式(2)中第一个和第三个方程可知N01=N10，这就证明了矩阵ROx的任意2 列中，数对01 和10出现的次数一定相等。

注：①由式(2)可知，ROx的任意2 列中，数对11 和00 出现的次数之差为N11−N00=2w−n；②定理1 说明，一个轨道矩阵的任意2 列构成的子矩阵的行向量中，数对00、01、10 和11 出现的次数实际上是由00、01 和11 这3 种数对确定的；③如果ROx是一个短轨道，且1 ＜|ROx|＜n，定理1的结论不一定成立。根据上面的性质，为简化问题，本文给出如下定义。

定义4设n维向量在循环群的作用下生成的旋转对称的长轨道为

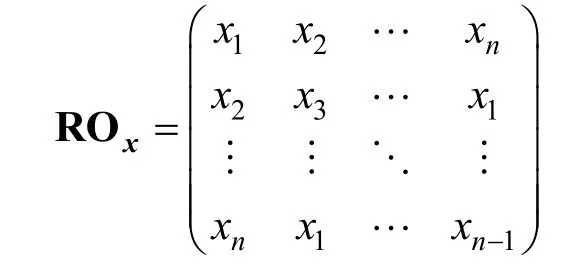
在ROx的第1 列和第列中，数对00、01、11 出现的次数分别为bk−1,1、bk−1,2、bk−1,3，则称如下的矩阵

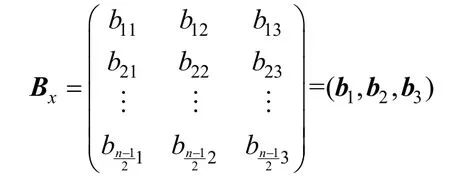
为旋转对称轨道ROx的数对分布矩阵。

特别地，若0r和1r分别表示r个连续的0和r个连续的1 构成的行向量，则轨道{0n}和{1n}的数对分布矩阵为矩阵，即

对于n维向量x=(x1,x2,…,xn)，若，则容易证明在循环群Cn的作用下生成的旋转对称轨道的数对分布矩阵为

文献[15]给出了旋转对称弹性函数的支撑矩阵的性质，并给出了旋转对称2-弹性函数的等价刻画，但是不能给出具体的构造方法，为了构造出具体的旋转对称2-弹性函数，本文首先给出定理2。

定理2若t为正整数，当n=4t−1时，则对任意的汉明重量为2t的向量，生成的轨道矩阵的数对分布矩阵为

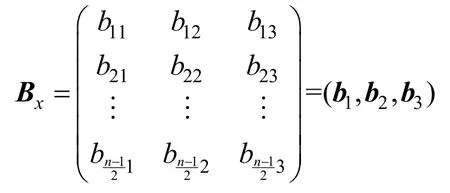
证明当n=4t−1时，对任意的汉明重量为的向量x=(x1,x2,…,xn)，由于2t与4t−1互素，故该向量生成的旋转对称轨道一定是长轨道。根据轨道矩阵对应的数对分布矩阵的定义，在定理1 中，向量x=(x1,x2,…,xn)的汉明重量为w=2t，由式(2)可得，N11−N00=2w−n=1，这说明向量x=(x1,x2,…,xn)所在的轨道矩阵中由任意2 个列向量di和dj构成的n×2维矩阵的行向量构成的数对11 的个数N11总比数对00 的个数N00多1。令i=1，j跑遍集合{2,3,…,2t}，可得，即向量。证毕。

4 4t−1 元旋转对称2-弹性函数的一个新的等价刻画

定理3对于式(1)所定义的函数f(x)，则f(x)是旋转对称2-弹性函数的充分必要条件是集合T满足如下2 个条件。

1)T可以分解为集合S0和S1，使T=S0∪S1，其中

且|S0|=|S1|，其中，m和m'为非负整数，l1,l2,…,lm和s1,s2,…,sm'在集合{0,1,…,2t−1}中取值。

2)S0中不同的旋转对称轨道对应的数对分布矩阵之和与S1中不同的旋转对称轨道对应的数对分布矩阵之和相等。

证明必要性。如果f(x)是旋转对称2-弹性函数，这意味着f(x)既是2-弹性函数，也是旋转对称函数。由于f(x)是2-弹性函数，根据弹性函数与正交表大集间的等价关系可知，{1f,0f}是上的一个强度为 2 的正交表大集，故1f和0f都是 OA(2n−1,n,2,2)。由于f(x)是旋转对称函数，1f和0f一定都是若干个旋转对称轨道的并集。另一方面，对1f中的旋转对称轨道进行分类，将向量的汉明重量为偶数的所有旋转对称轨道记为S0，显然S0可表示为一些旋转对称轨道的并集，即

对0f中的旋转对称轨道进行分类，将其中向量的汉明重量为奇数的旋转对称轨道记为S1，显然S1也可表示为一些旋转对称轨道的并集，即

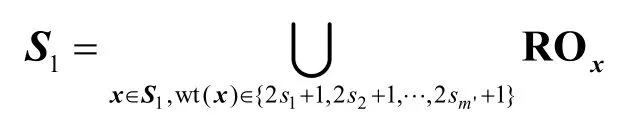
其中，m和m'为非负整数，l1,l2,…,lm和s1,s2,…,sm'在集合{0,1,…,2t−1}中取值，n=4t−1，故f(x)的支撑集可以表示为，由f(x)是平衡的，可知|S0|=|S1|，故条件1)成立。而由是一个OA(2n−1,n,2,n−1)可知，也是一个OA(2n−1,n,2,2)，这就意味着在的任意2 列中，数对00、01、10、11 出现的次数均为 2n−3，由于1f和都是OA(2n−1,n,2,2)，因而在1f的任意2 列中，以及在的任意2 列中，数对00、01、10、11 出现的次数均为 2n−3，注意到

这说明S0中不同的旋转对称轨道对应的数对分布矩阵之和与S1中不同的旋转对称轨道对应的数对分布矩阵之和相等，即条件2)成立。必要性证毕。

充分性。由于f0(x)=x1+x2+…+xn是一个n元旋转对称弹性函数，故当条件1)成立时，注意到T=S0∪S1，且S0和S1均为一些旋转对称轨道的并集，因而T可以看作一个旋转对称函数的支撑集，从而条件1)中定义的函数f(x)是一个旋转对称函数；再由f0(x)是弹性函数以及T=S0∪S1和|S0|=|S1|可知，f(x)是平衡函数；由正交表与弹性函数的关系，只需证明1f是强度为2 的正交表即可。

根据条件2)，由S0中不同的旋转对称轨道对应的数对分布矩阵之和与S1中不同的旋转对称轨道对应的数对分布矩阵之和相等可知，式(1)所定义的函数f(x)的支撑矩阵1f的 1 列分别与第列正交，再根据旋转对称函数的支撑矩阵的性质以及引理3 可知，f(x)的支撑矩阵1f是一个OA(2n−1,n,2,2)。充分性证毕。

由定理3 可知，旋转对称2-弹性函数的构造等价于寻找满足定理3 条件的集合T，其中条件1) 是为了保证所构造的函数是平衡的旋转对称函数，条件2) 是为了保证所构造的函数是2-弹性的，利用定理1 和定理2 得到的结果，借助于定理3，可以构造旋转对称2-弹性函数的无穷类，结合下面的例子，来说明本文方法的有效性。

5 一个构造性的例子

以7 元旋转对称2-弹性函数的构造为例，来说明本文的定理在一类4t− 1元旋转对称弹性函数的构造中的应用。由引理1 以及文献[13]中的计算可知，若n=4t− 1为素数，则循环群Cn在上的作用形成的轨道中，只有2 个短轨道{0n}和{1n}，其他的均为长轨道。特别地，对于循环群作用在上，形成和这2 个短轨道，以及18 个长轨道。为了方便，本文将旋转对称轨道及其对应的数对分布矩阵分别表示为

行向量的汉明重量为3 和4 的轨道有如下10 个，其中，对应的数对分布矩阵。

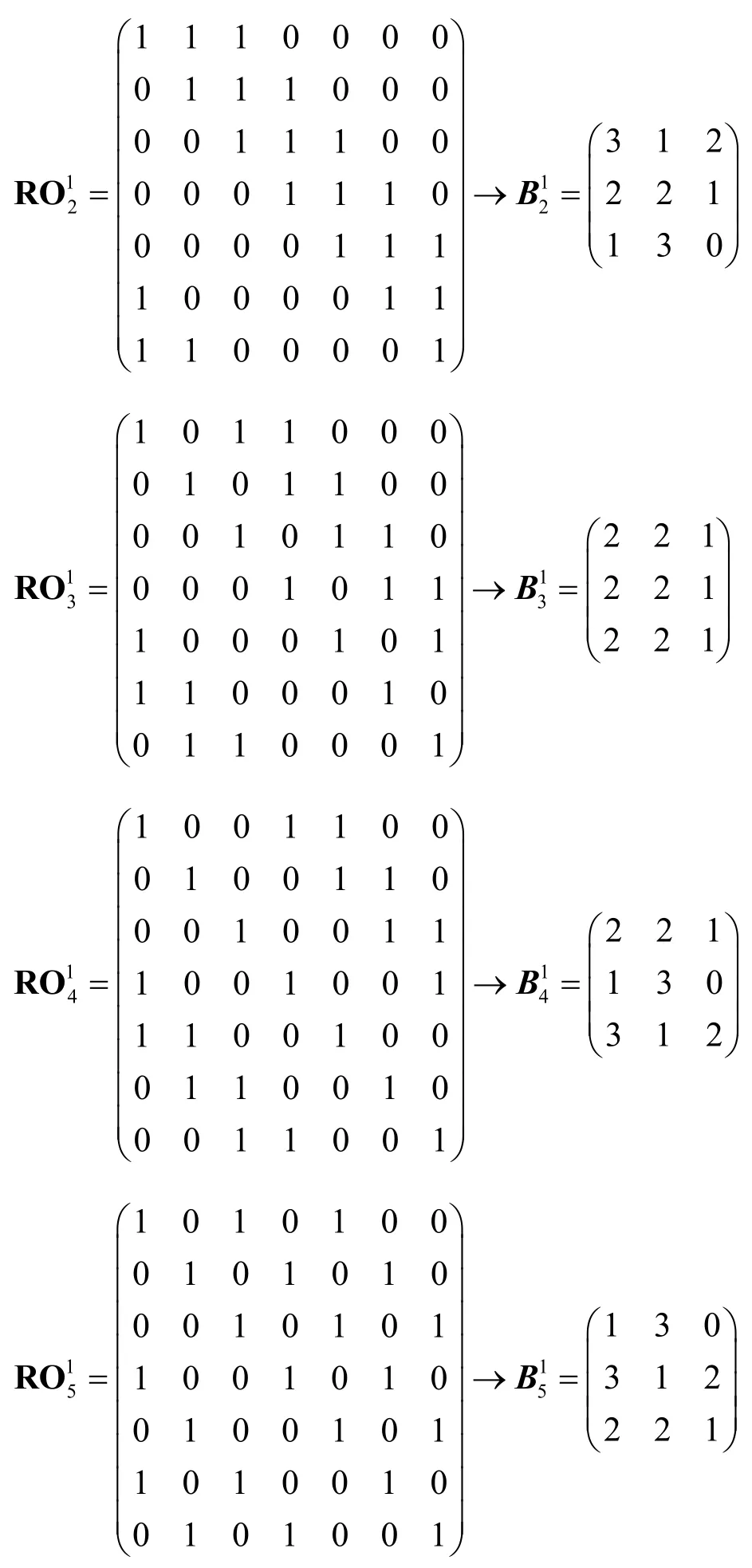
由定理3 可知，要构造不同的7 元旋转对称2-弹性函数，关键在于确定不同的S0和S1。若S0和S1中分别有2 个轨道，且其中之一是短轨道时，可以有如下的7 种方案。

当S0和S1按照上面的 7 种方案确定，取T=S0∪S1时，有|S0|=|S1|，对于式(1)定义的f(x)，根据定理3 可知，f(x)均为旋转对称2 阶弹性函数。其中方案 1 确定的T=S0∪S1=，可以根据T中的向量计算所构造函数的代数正规型。当变元个数n=4t−1较大时，如何根据所构造函数的支撑矩阵得到其代数正规型，计算其非线性度是一个有待进一步解决的问题。

6 结束语

旋转对称函数由于其特殊的结构及其广泛的应用受到越来越广泛的研究，关于旋转对称1-弹性函数的构造与计数已经有较多的结果，本文基于旋转对称轨道的数对分布矩阵的性质，给出了一个旋转对称2-弹性函数的直接构造方法，该方法能构造出无穷多个旋转对称2-弹性函数，但是由于所给出的函数都是以支撑集的形式给出的，因而不能给出所构造函数的具体的代数正规型，或者说，需要烦琐的计算转换才能给出代数正规型，因而也就不能直接地给出其代数次数。其次，已有的一些文献对所构造的RSBF 是基于择多函数得到的，因而对非线性度的估计计算有较多的数学工具可用，而本文构造的函数是通过修改线性函数f0(x)=x1+x2+…+xn的支撑集而得到的，对其非线性度的计算也有较大的难度，这也是本文的一个不足。寻找有效地计算本文中所构造的旋转对称2-弹性函数的代数表达式与非线性度将是下一步要解决的问题。