超声波透金属通信中子载波快速筛选比特填充算法
(北京交通大学电子信息工程学院,北京 100044)
1 引言
近年来,有关超声波透金属通信的研究引起了广泛关注[1]。在一些状态监测和无线传感应用中,需要与密封金属容器内部进行数据交换和能量传输,由于金属的静电屏蔽和趋肤效应,电磁波不能有效地穿透金属,而在金属上钻孔会破坏金属结构的完整性,具有潜在危险,如有毒化学品的泄漏、压力或真空的损失等,因此,许多研究利用超声波作为载体实现透金属通信和功率传输[2-4]。压电换能器(PZT,piezo-electric transducer)是超声领域的常用元件,其利用电介质的压电效应,将电能与声能相互转换,具有体积小、效率高的优点。文献[5]提出了超声透金属通信的单跳、双跳、反射功率结构。超声波透金属通信的信道结构一般由金属壁和固定于金属壁两侧的PZT 组成,发射端位于金属外侧,容易接触和修改;接收端位于金属内部,受到安装环境、体积、功率的限制,难以接触并且要保持长期稳定运行。超声波由发射端PZT 产生,透过金属传播后被接收端PZT 吸收,然而,超声波并不能被接收端PZT 完全吸收,一部分超声波会反射回发射端,再由发射端反射回来,如此往复进行,导致接收端收到多个超声波信号。这种回波现象类似于无线通信中的多径效应,使超声波透金属通信信道具有频率选择性。
为了消除频率选择性衰落的影响,文献[6]采用基于回波消除的预失真滤波器抑制信道回波,实现了超声波透金属高速通信,将数据速率从50 kbit/s提高到1 Mbit/s。在文献[6]的基础上,文献[7]建立了更精确的信道模型,提高了回波消除技术的性能,并采用脉冲幅度调制实现了5 Mbit/s 的数据速率。正交频分复用(OFDM,orthogonal frequency division multiplexing)是一种被广泛应用的多载波调制技术[8-10],当OFDM 的子载波频率间隔小于信道的相干频率时,可将每个子信道视为平坦衰落信道,不需要使用复杂的均衡技术就能消除信道频率选择性衰落的影响。由于信道的频率选择性衰落,OFDM 系统中各个子信道的信噪比(SNR,signal-to-noise ratio)变化较大,若在OFDM 系统的所有子载波上分配相同的比特数,即所有子载波采用相同的调制方式,那么低SNR 子信道的误比特率(BER,bit error rate)会很高,而高SNR 子信道仍可分配更多比特数,因此,必须采用功率或比特加载技术调整各子信道的功率或比特数。
文献[11]提出了一种固定功率的速率自适应比特加载算法的变体,仿真结果表明,在超声透金属通信中,达到的数据速率明显大于非自适应调制。文献[12]提出固定功率的Chow 算法,将现有超声技术的数据速率提高了300%,达到15 Mbit/s。文献[13]研究发现利用比特和功率混合加载技术,理论上可将超声透金属通信的数据速率提高到信道容量的80%,但是并未给出具体的实现过程。文献[14]将多输入多输出技术与OFDM 相结合,并为子载波分配不超过BER 阈值的最大比特数,在超声波透金属通信中实现了50%的理论信道容量。文献[15]研究了多信道超声穿墙通信系统的资源分配问题,提出一种新的功率分配算法,相比于传统比特加载技术和贪婪比特填充技术能达到更高的数据速率,但是算法复杂度较高。文献[16]将压电换能器嵌入金属中,组成无线传感网络,实现了数据和功率的同时传输。比特和功率加载技术大大提高了超声波透金属通信的数据速率,同时增加了实现复杂度,使加载技术在超声波透金属通信场景中的应用更加困难。
本文在固定功率、BER 阈值和不同比特增量的限制下,对已有的贪婪算法进行改进,提出一种用于超声波透金属通信的子载波快速筛选的比特填充算法。通过BER 近似公式和泰勒展开推导出子载波BER 增量的近似表达式,将其作为贪婪比特填充算法中子载波的选择依据,先筛选子载波再计算其BER,省去了对大部分子载波新BER 的计算,降低了贪婪算法的复杂度。仿真结果表明,所提算法可达到贪婪比特填充算法的数据传输速率,且算法的计算量更低。
2 信道和系统模型
本节分析了超声波透金属通信信道的特点,介绍了基于夹板式压电换能器(SPPT,sandwiched plate piezoelectric transformer)声电信道分析模型[17]和OFDM 多载波系统模型。
2.1 基于SPPT 的声电信道分析模型
图1 为基于SPPT 的超声透金属通信的信道结构[3]。金属两侧的PZT 由耦合剂进行同轴固定,PZT决定了超声波的频率,耦合剂可提高超声波的传输效率。超声波经过耦合剂、金属、耦合剂传输,每一层都会产生反射波,反射波经过各层也会产生反射波,因此必须仔细选择PZT 和耦合剂,使其特性声阻抗尽可能接近,以减少反射损耗和多路径传播。接收端收到的反射波被称为回波,回波导致接收信号在时域产生线性失真,在频域表现为频率选择性(振幅失真)和群时延失真(相位失真)。信道的频率选择性主要由金属的自然模态产生,金属壁越厚,相邻回波的时间间隔越长,则信道的频率选择性越严重;群时延失真使回波信号的色散增大,使回波产生拖尾现象[3]。
一般认为超声波透金属通信信道是准静态的,具有近乎无限的相干时间,可以忽略信道的多普勒扩展[1,3]。受收发端配置、金属厚度、安装误差、实际通信环境等影响,接收端回波的个数通常需要根据实际测量来确定。为了简化分析,假设接收端收到的最大回波数为9 个(包含第一次的接收信号),考虑到拖尾现象,则信道时延扩展可近似为

其中,dm为金属厚度,cs=5 838m/s 为声波在金属中的传播速度。从式(1)可以看出,随着金属厚度的增加,信道时延扩展逐渐增大,信道相干带宽为信道时延扩展的倒数,因此,信道相干带宽逐渐降低,OFDM的子载波频率间隔逐渐降低。过低的子载波频率间隔导致系统对多普勒频移和相位噪声敏感,因此,大部分有关超声透金属通信的研究所考虑的金属厚度不超过100 mm,仅文献[5]研究了金属厚度为150 mm的超声通信,实现了300 bit/s~5 kbit/s 的低速通信。

图1 基于SPPT 的超声透金属通信的信道结构
图2给出了基于SPPT分析模型的超声波透60 mm金属通信的信道功率增益。

图2 超声波透60 mm 金属通信的信道功率增益
从图2 可以看出,信道的整体功率增益较低,且具有严重的频率选择性。在PZT 谐振中心频率4.28 MHz 处,功率增益为−10 dB,而在频率6MHz处,功率增益减小为−50 dB。由于信道的功率增益较低,通过信道的信号会产生很大的衰减,不利于接收端对信号的接收,因此需要对信号的衰减进行补偿。信道功率增益补偿如图3 所示,通常在发射端加入换能器驱动,并在接收端加入低噪放大器(LNA,low noise amplifier)进行联合补偿。本文主要研究比特加载算法,不考虑电路方面的实现,所以假设换能器驱动和LNA 能有效地补偿信道带来的信号衰减,将换能器驱动和LNA 的联合增益(单位为dB)选为信道平均增益(单位为dB)的相反数。这样补偿后的信道平均功率增益为0 dB,将其作为仿真使用的信道。
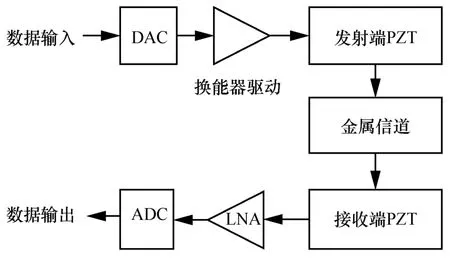
图3 信道功率增益补偿示意
2.2 OFDM 多载波系统模型
OFDM 技术是应用最广的一种多载波传输方案,由于其不需要使用复杂的均衡技术就能消除信道频率选择性衰落的影响,近年来被广泛应用于超声波透金属通信中。设OFDM 系统有N个子载波,每个子载波可单独进行调制。设调制后的复信号为d=[d0,d1,…,dN−1]T,其中di(i=0,…,N−1)为从星座图中等概率选择的调制信号,则每个子载波的平均功率相同。d经过傅里叶逆变换得到OFDM 符号的时域采样信号为x=FHd,其中F为N×N的快速傅里叶变换(FFT,fast Fourier transform)矩阵,(⋅)H为厄米特转置。通常选择x的最后NCP个数据作为循环前缀(CP,cyclic prefix)加到数据开头,这样可消除OFDM 的符号间干扰,同时可将信道的线性卷积转换为循环卷积。
信号经过信道传输后到达接收端,接收端从收到的数据中移除循环前缀,得到接收信号。由于超声波透金属通信信道是准静态的,信道状态在一个或多个OFDM 符号持续时间内保持稳定,因此接收信号为

其中,H表示信道状态的N×N循环矩阵,表示加性高斯白噪声向量,IN表示N×N单位矩阵。接收信号经过FFT 后得到

3 快速筛选子载波的比特填充算法
加载技术所解决的分配问题通常分为两类[19],一是利润最大化问题,在达到目标数据速率的同时实现功率最小化;二是速率最大化(RM,rate maximization)问题,在给定最大功率限制下实现数据速率最大化。在RM 问题中,最大功率限制的一种简单情况就是为各子载波分配相同的功率,并为各子载波分配不同的比特数。通常在实际应用中,分配的比特数为整数,且要求BER 不超过某个阈值,因此RM 问题为整数规划问题,由下列优化问题表示[20]。

其中,bi∈N+表示第i个子载波分配到的比特数,Pi表示第i个子载波的BER,表示一个OFDM 符号的平均BER,PT表示给定的BER 阈值。Pi由子载波符号信噪比和调制方式决定,子载波符号信噪比定义为,其中,ps为子载波符号平均功率。本文所有信噪比均指符号信噪比,以下简称信噪比。
3.1 贪婪比特填充算法
贪婪比特填充算法作为解决RM 问题的一种经典分配算法,复杂度较高,一般通过预分配方法降低贪婪算法的迭代次数[21]。由于要迭代计算,贪婪算法的比特分配结果具有一定时延,无法满足快速时变信道和低时延的要求,而超声透金属通信对实时性要求不高,且信道处于准静态,因此贪婪算法能很好地适用于超声透金属通信中。此外,贪婪算法是对每个子载波进行比特分配,因此超声透金属信道的频率选择性衰落不会对算法产生影响。
贪婪比特填充算法主要分为两步,第一步为各子载波分配初始的比特数,第二步对子载波进行筛选并分配额外的比特数。初始比特数的分配通常采用基础分配算法。基础分配算法计算出给定BER 阈值时进行不同调制所需的最低SNR,然后利用子载波信噪比和查表法,为各子载波分配初始比特数。本文考虑2 种调制方式,分别为二进制相移键控(BIT/SK,binary phase shift keying)和矩形灰度编码的多进制正交幅度调制(MQAM,multiple quadrature amplitude modulation),相应的BER 分别如式(5)和式(6)所示[22]。

其中,M=4m(m=1,2,3,…),Q(⋅)表示Q函数。如果不确定第i个子载波的调制方式,可将第i个子载波的BER 写为Pi,当子载波信噪比太低,可以将该子载波置空,即不在该子载波上传输比特。根据式(5)和式(6)可得,在给定BER 阈值和调制方式时的信噪比为

其中,Q−1(⋅)是Q函数的反函数,为给定BER阈值时进行BIT/SK 调制所需的最低SNR,为给定BER 阈值时进行MQAM 调制所需的最低SNR。图4 为不同调制方式下BER 与SNR 的关系,标注了在PT=10−6时不同调制方式所需的最低信噪比,例如,当时,子载波为 BIT/SK 调制。
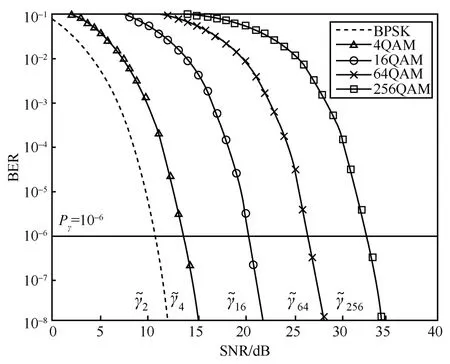
图4 不同调制方式下BER 与SNR 的关系
利用式(7)和式(8)可以得到基础分配算法所需的SNR 查表值。在进行初始比特数分配后,每个子载波的BER 都小于BER 阈值,因此平均BER 小于BER 阈值,满足式(4)的约束条件。基础分配算法使贪婪比特填充算法不需要从零开始为子载波分配比特数,大大降低了算法的计算量。
在基础分配算法后,由于平均BER 未达到BER阈值,仍有增加的空间,因此可以为子载波分配额外的比特数使平均BER 逼近BER 阈值。
贪婪比特填充算法筛选子载波的方法是计算所有子载波的BER 增量,然后选择具有最小BER增量的子载波,并为其分配额外比特数。某个子载波(假设为第k个子载波)的BER 增量为
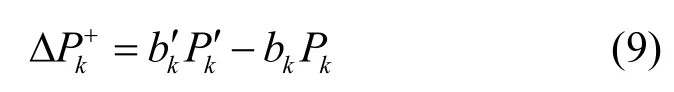
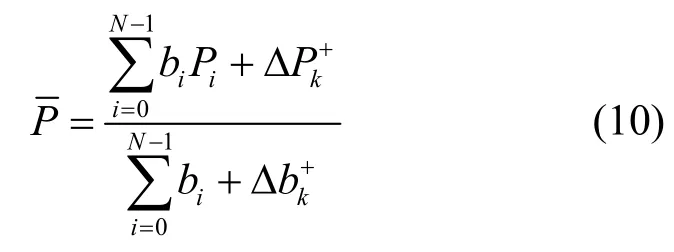
1)按基础分配算法为各子载波分配初始的比特数。
2)计算子载波的BER 增量。
3)选择具有最小BER 增量的子载波,提高其调制方式后计算平均BER,并将其剔除。
4)若平均BER 大于BER 阈值,停止;否则,转到步骤3)。
根据式(5)和式(6)可以发现,子载波的BER 增量仅与子载波SNR 和调制方式有关,并没有涉及信道的整体状态,这意味着即使超声波透金属通信信道处于严重的频率选择性衰落,贪婪比特填充算法也不会受到影响。但是,利用式(5)和式(6)计算子载波BER,需要开方和Q函数计算,当OFDM 子载波数增加时,贪婪比特填充算法的计算量会变得很大,在实际应用中的实现难度变高。例如,对于金属壁内的超声通信设备,不仅需要高速数据传输,还受到功率的限制。
子载波的比特数由所选调制方式决定,在实际应用中一般取整数。本文考虑的调制方式为空载波、BIT/SK 和MQAM,相对应的比特数分别为0、1 和2m(m=1,2,3,…),相邻调制方式的比特增量不同,空载波到BIT/SK 和BIT/SK 到4QAM 的比特增量为1 bit,其他相邻调制方式的比特增量为2 bit。由于比特增量不同,式(10)中分母的变化不一定相同。贪婪比特填充算法在选择子载波时仅考虑了BER 增量,在不同比特增量的情况下,分配额外比特所带来的平均BER 的提升并不一定最小。因此,为了达到更加精确的子载波筛选,必须考虑不同比特增量所带来的影响。
3.2 快速筛选子载波的贪婪比特填充算法
在贪婪比特填充算法中,需要计算所有子载波的BER 增量,每个子载波都要计算两次BER,分别为原BER 和新BER,但是只有部分子载波的调制方式被提高,而其余子载波的调制方式保持不变,计算这些子载波的新BER 带来了额外的计算量。通过省去这部分子载波新BER 的计算,可以降低算法的计算量,因此,需要一种算法将提高调制方式的子载波筛选出来。
由图4 可以看出,BER 随SNR 的变化近似为负指数函数。由于式(5)和式(6)过于复杂,难以对变化曲线进行分析,因此利用BER 近似公式分析。MQAM 和 BIT/SK 的BER 近似公式分别为[23]
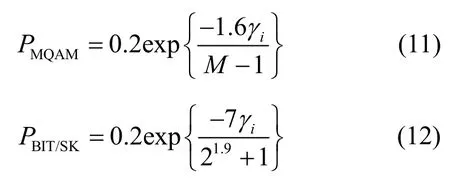
将式(11)和式(12)代入式(9)得
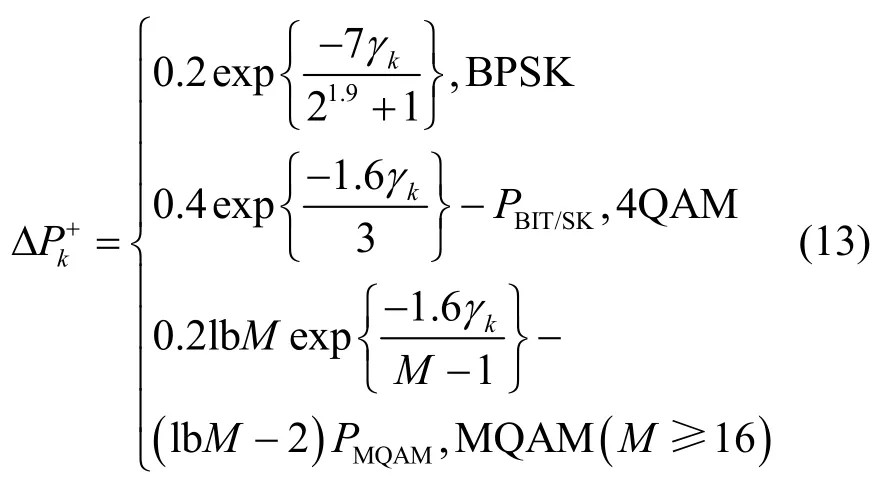
其中,BIT/SK 和MQAM 表示第k个子载波提高后的调制方式。在利用贪婪比特填充算法分配额外的比特数之前,需要先计算各子载波的Pk和平均BER,因此,在式(13)中只需利用BER 近似公式替换子载波的新BER。
由3.1 节的分析可知,只利用BER 增量筛选子载波并不准确,不同的比特增量会影响平均BER 的值。因此,为了消除对平均BER 的影响,将式(10)代入式(4)的约束条件,并为分母添加1 bit,为分子添加一个参数PT,可得

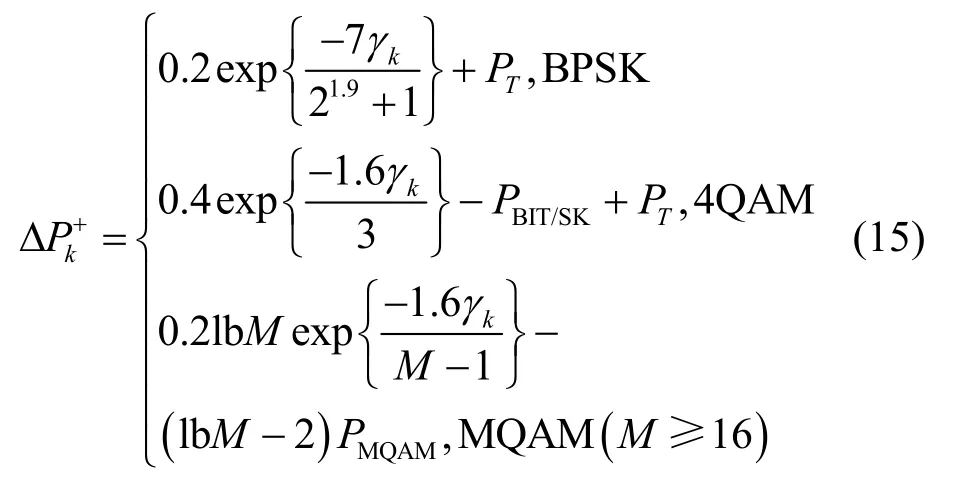
对式(15)进行泰勒展开可得
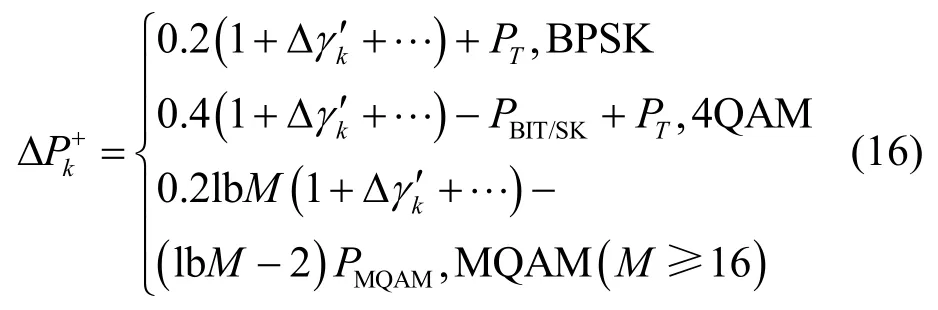
当仅考虑泰勒展开式的第一项时为最简单选择方法,此时,各种调制方式下的大小关系固定,按调制方式从低到高,依次选择具有最小的子载波。需要注意,如果利用式(16)计算平均BER会产生较大的误差,甚至可能使平均BER 超过BER阈值,因为截断的泰勒展开式小于精确值。因此,精确的BER 需要使用BER 公式计算,或者在误差允许范围内使用BER 近似公式计算。本文选择使用BER 公式计算。
与贪婪比特填充算法相比,快速筛选子载波的贪婪比特填充算法先对子载波进行筛选,然后计算其提高调制方式后的新BER。所提算法的主要流程如下。
1)按基础分配算法为各子载波分配初始的比特数。
2)截取式(16)的前L项做近似,计算各子载波的BER 增量。
3)选择具有最小BER 增量的子载波,计算其提高调制方式后的新BER 和平均BER,并将其剔除。
4)若平均BER 大于BER 阈值,停止;否则,转到步骤3)。
3.3 算法复杂度分析
与贪婪比特填充算法相比,所提算法的不同之处在于步骤2)和步骤3)。步骤2)截取泰勒展开式的前L项做近似,计算各子载波的BER 增量;步骤3)利用BER 增量,筛选子载波并提高其调制方式。所选的泰勒展开式项数越多,BER 增量的精度越高,计算量也越大。计算单个子载波的加权信噪比仅需一次乘法操作,计算截断的泰勒展开式需要2(L−2)次乘法操作和(L−1)次加法操作。在计算完加权信噪比和泰勒展开式部分后,计算单个子载波BER 增量的总操作次数为

其中,A表示加法操作(或减法操作),M表示乘法操作。可以发现,本文所提的子载波筛选算法对于子载波BER 增量的计算仅需少量加法和乘法操作,不需要开方和Q函数运算,计算速度提高。利用BER 增量筛选出子载波后,再用BER 公式计算子载波的真实BER,避免了对所有子载波BER 的计算,使算法整体的运算速度更快。
需提高调制方式的子载波数越少,算法的计算量越小。需提高调制方式的子载波数,也就是所提算法中步骤3)的迭代次数,与信道状态和调制方式有关,只能通过仿真计算得到,将在第4 节讨论。这里考虑一种极端情况,假设所有子载波都需要提高调制方式,此时不仅需要计算所有子载波的精确BER,还需要计算所有子载波的,所提算法的计算量反而会增大。幸运的是,贪婪比特填充算法首先为各子载波分配初始的比特数,保证了所有子载波的BER 都小于BER 阈值,如果所有子载波都提高了调制方式,那么平均BER 会超过BER 阈值,因此上述的极端情况不会出现。
4 仿真与讨论
本节对快速筛选子载波的贪婪比特填充算法进行仿真,并与其他算法对比了系统的吞吐量和复杂度。超声波透金属通信信道采用基于SPPT 的分析模型,并对信道进行功率补偿。采用OFDM 多载波系统,为了简化OFDM 的参数设置,设置OFDM 的子载波数为4 096 个,OFDM 子载波间隔统一为1 kHz,CP 长度为原始OFDM 符号的,此时频谱效率仅降低20%。设置仿真金属厚度为10~80 mm,当金属厚度为80 mm 时,可以计算出信道时延扩展约为245μs,略小于CP 的250μs。根据第3 节的算法分析,选择调制方式为BIT/SK和MQAM(M=4,16,64,256)且子载波可以为空,选择5 种不同精度的泰勒展开式(L=1,2,3,4,5),BER 阈值为10−6。对于每个金属厚度和每个SNR 进行蒙特卡罗仿真103次后取平均。本文将所提算法与基础分配算法、贪婪比特填充算法、增量分配算法(IAA,incremental allocation algorithm)[20]和基于间隔的比特加载算法[18]进行比较。
图5 为不同金属厚度下不同比特填充算法的平均吞吐量和SNR 的关系。从图5 可以看出,随着SNR 的增加,吞吐量逐渐提高,且基础分配算法为所有算法的吞吐量下限。从图5 可以直接分辨出L=1的吞吐量曲线,当L≥2时,算法的吞吐量已经接近贪婪比特填充算法。随着L的提高,所提算法的吞吐量逐渐接近贪婪比特填充算法。在SNR=24 dB 处,当L=3时,所提算法的吞吐量与贪婪比特填充算法仅相差十几比特;当L=5时,仅相差约1 bit。
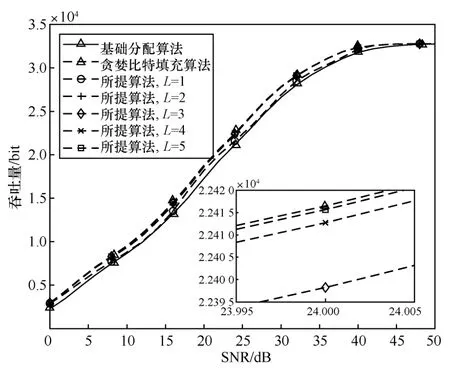
图5 平均吞吐量和SNR 的关系
图6 为不同比特加载算法下的相对吞吐量和SNR 的关系,相对吞吐量是指相对于基础分配算法所增加的吞吐量。整体上看,随着SNR 的增加,除L=1的所提算法的曲线之外,其余算法的相对吞吐量都有先增后减的趋势,且在SNR 为15~30 dB 达到最大。与基于间隔的比特加载算法相比(可调参数为间隔阈值ST),随着可调参数的提高,所提算法的相对吞吐量提高得更快,在L=3时已经接近IAA。另外,仿真发现,调制方式越多,SNR 越低,IAA 和基于间隔的比特加载算法的迭代次数越多,这是因为这2 种算法是从所有子载波处于最大调制方式时开始迭代,达到最优结果需要更多的迭代次数。从图6 还可以发现,在仿真的SNR 范围内,最大相对吞吐量不是IAA 就是L=4的所提算法,这是因为这2种算法都基于贪婪策略,并不能保证整体最优,IAA 通过移除比特逼近最优解,所提算法通过填充比特逼近最优解,因此可以考虑将比特填充算法与比特移除算法相结合,达到更优的比特分配结果。

图6 不同比特加载算法下的相对吞吐量和SNR 的关系
图7 为不同比特填充算法下的系统吞吐量和金属厚度的关系,设置SNR 为30 dB。从图7 可以看出,在不同比特填充算法下,随着金属厚度的增加,系统吞吐量逐渐增加。这是因为随着金属厚度的增加,相同带宽内金属的自然模态数量越多,模态数量增加所带来的SNR 提高量超过了模态周期缩小所带来的SNR 降低量[3],因此信道容量会逐渐提高,从而使系统吞吐量逐渐提高。
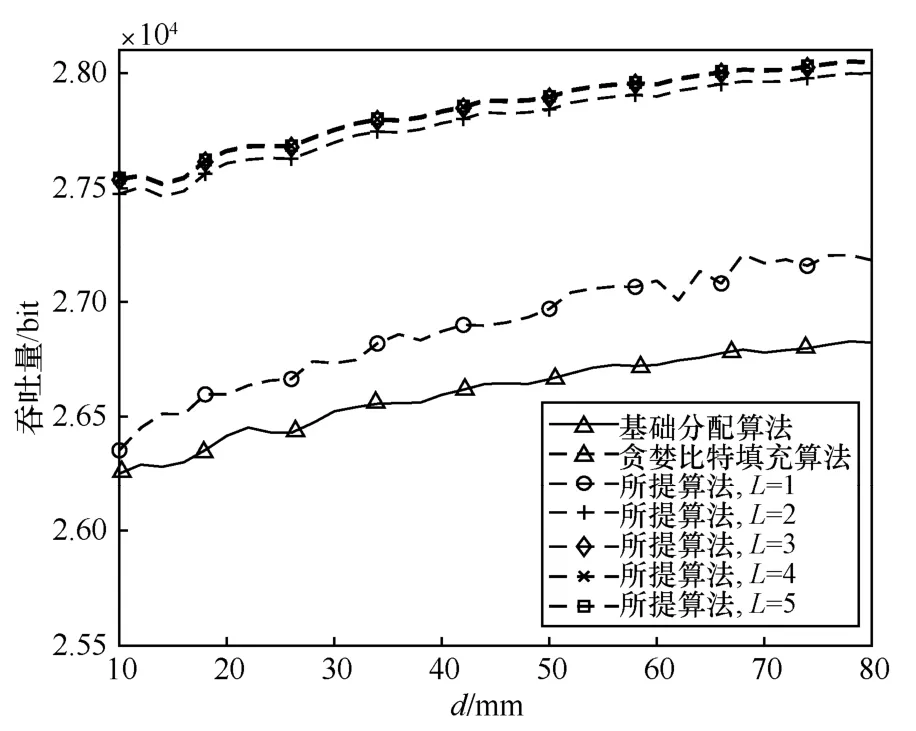
图7 不同比特填充算法下的系统吞吐量和金属厚度的关系
图8 为不同金属厚度下比特填充算法的平均迭代次数和SNR 的关系。迭代次数为重复进行所提算法步骤3)的次数。从图8 可以看出,随着SNR的增加,迭代次数呈下降的趋势,最大迭代次数为900 次左右,仅有约的子载波提高了调制方式,这意味着与贪婪比特填充算法相比,所提算法节省了约的子载波BER 的计算,算法计算量大大降低。与贪婪比特填充算法相比,L=1的所提算法具有最低的迭代次数,但迭代次数的波动较大。在SNR=14 dB 附近,L=1的所提算法迭代次数不到100 次,结合图6 可以发现,此时,所提算法的系统吞吐量接近基础分配算法,相对吞吐量较低,这是因为有一部分信噪比很低的空子载波,所提算法优先提高所有空子载波的调制方式,导致平均BER 很快地达到BER 阈值。同样,在SNR=28 dB和SNR=38 dB 附近,信噪比最低的子载波分别为4QAM 和16QAM 调制,提高它们的调制方式使平均BER 快速变大。随着L的增大,所提算法的迭代次数波动逐渐变小,L=3时算法迭代次数已经接近贪婪比特填充算法。
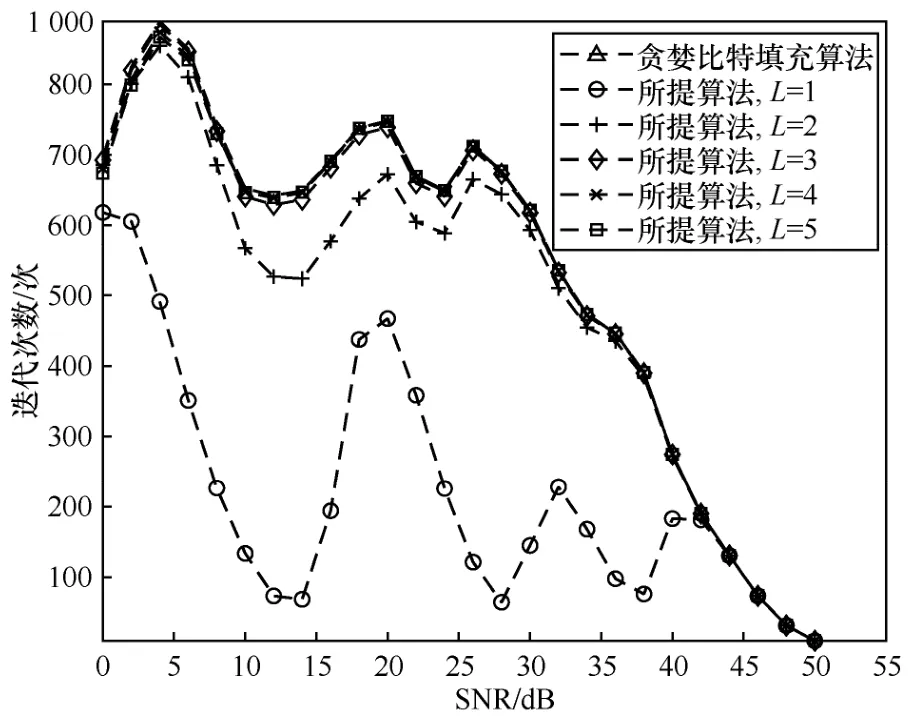
图8 不同比特填充算法下的平均迭代次数和SNR 的关系
图9 为不同比特填充算法下的平均迭代次数和金属厚度的关系,根据图8 将设置SNR 为迭代次数变化较平坦的10~30 dB。从图9 可以看出,各种填充算法的平均迭代次数保持稳定,不随金属厚度变化,这表明各种比特填充算法没有受到不同厚度金属下信道频率选择性衰落的影响,与基于间隔的比特加载算法相比,具有很强的稳定性。

图9 不同比特填充算法下的平均迭代次数和金属厚度关系
5 结束语
本文利用SPPT 分析模型,在固定功率分配、BER 阈值和不同比特增量的限制下,提出一种用于超声波透金属通信的子载波快速筛选贪婪比特填充算法。所提算法利用截断的泰勒展开式求出子载波BER 增量作为子载波选择依据,省去了对所有子载波精确BER 增量的计算。仿真表明,所提算法省去了约的子载波BER 的计算,算法计算量大大降低,且系统吞吐量并未有明显下降,在截断长度L=3时与贪婪比特填充算法仅相差十几比特。同时,仿真验证了系统吞吐量随金属厚度的增加而逐渐增大这一现象。
与IAA 的比较可以发现,比特填充算法和IAA 都基于贪婪策略,并不一定能得到全局最优解,因此可以考虑将比特填充算法与比特移除算法相结合,达到更优的比特分配结果。而与基于间隔的比特加载算法相比,所提算法不受信道频率选择性衰落的影响,具有很强的稳定性。因此,所提算法不仅实现简单,稳定性高,而且算法性能优异,在超声透金属通信中具有很强的应用前景。

