立足基础巩固 强化能力提升———平面向量的教学要点

◇ 甘肃 杨春萍

平面向量在高考中既有直接考查的题型,也有间接考查的题型.直接考查是以向量基础知识为视角,题目难度不大,以中低档难度为主;间接考查主要考查向量与其他知识的交会,以及利用向量工具解题.因此向量的教学中要落实好如下几方面内容.

1 夯实基础知识

平面向量中所涉及的基础知识包括向量的概念、向量的模、向量的运算、向量基本定理等,教学中要强化各知识点之间的关系及其推广.从近年高考题来看,向量命题基本都围绕这些基础知识展开.

例1已知非零向量a,b满足|a|＝2|b|,且(a－b)⊥b,则a与b的夹角为________.

解析

方法1根据题目条件(a－b)⊥b可构造如图1所示直角三角形,又因为|a|＝2|b|,所以a与b的夹角为60°.

方法2本题也可采用常规解法,由(a－b)⊥b知(a－b)b＝0,即所以a与b的夹角为60°.

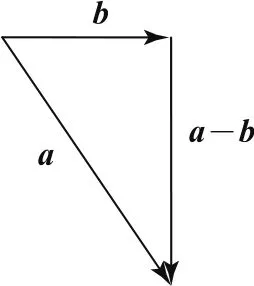
图1

点评

本题考查了向量的基本运算、利用数量积求夹角,两种方法难度虽然都不大,但方法1通过构造图形更显直观简捷,小题小算.

2 掌握基本技能

平面向量与其他知识的交会是高考命题的常见形式.基本技能体现在问题求解中要解开向量外衣,挖掘问题的本质.

TYRONE:Well, if you split the money I gave you with him,like a fool-[20]129

例2(2018年全国卷Ⅰ)平面向量a,b,e,其中a是非零向量,e是单位向量,且a与e的夹角为60°,b满足b2－4be＋3＝0,则|a－b|的最小值是( ).

解析

方法1由b2－4be＋3＝0得(b－e)(b－3e)＝0,即(b－e)⊥(b－3e).

图2

构造图形,如图2所示,设a在射线OM上所所以CB⊥EB,即点B在以CE为直径、D为圆心的圆上,过点D作射线OM的垂线,垂足为A,且交圆D于点B′,所以当点B位于B′时,|a－b|＝|AB′|最小.

在Rt△OAD中,∠AOD＝60°,|OD|＝2,所以.

方法2由b2－4be＋3＝0,可得b2－4be＋4e2＋3＝4e2,即(b－2e)2＝1,则可据此构造圆.此法与方法1形异质同,过程略.

点评

本题以向量为背景考查了直线和圆的位置关系,解题的关键是构造圆.在平面向量问题中,若出现模为定值或直角等信息,均可构造圆来辅助解题.这也是高考对考生基本技能的考查.

3 明确基本思想

高考对平面向量中基本思想的考查包括“数形结合思想”与“化归转化思想”.主要体现在“数”化“形”、“形”化“数”、“未知”化“已知”等.

例3在矩形ABCD中,AB＝2,BC＝1,点E为BC的中点,点F在线段DC上.若且点P在直线AC上,则.

解析

方法1如图3,由向量加法的运算关系得设所以

图3

因为点P在直线AC上,设.

方法2以D为坐标原点,建立如图4所示平面直角坐标系,则D(0,0),A(0,1),B(2,1),C(2,0),设F(λ,0),则

点评

方法1中矩形各边所表示的向量为已知向量,通过引入参数λ,μ将未知向量用已知向量表示,再利用向量相等关系,求出参数的值.方法2利用坐标运算及向量共线的条件,引入参数,表示出动点坐标,再结合已知条件求参数的值或范围.

4 落实基本应用

高考中向量的应用主要体现在利用向量工具、辅助解答其他问题,如解析几何问题中的平行、垂直、共线、夹角等问题均可借助向量的坐标运算进行求解.

例4已知两点A(－1,0),B(1,0),若直线xy＋a＝0上存在点P满足AP⊥BP,则实数a满足的取值范围是________.

解析

方法1由AP⊥BP知点P在以AB为直径的圆上,圆的方程为x2＋y2＝1,则问题转化为圆与直线x－y＋a＝0有交点,即解得,故a的取值范围是[

方法2__由AP⊥BP,得.设P(m,m＋a),则a),由2m2＋2ma＋a2－1＝0.由Δ＝4a2－8(a2－1)≥0,解得所以a的取值范围是.

点评

方法1由线的垂直关系得到圆的性质,从而构造圆,利用直线与圆的位置关系求解.方法2利用坐标法表示出两向量数量积为0的方程,该方程是以点P的横坐标为变量,由方程有解,即判别式大于或等于0,求解结论.体现了向量的工具作用.