采用车载激光雷达的带状地物矢量化与结构特征提取
方莉娜,卢丽靖,赵志远,陈崇成
(1. 福州大学 地理空间信息技术国家地方联合工程研究中心,福建 福州 350002;2. 福州大学 空间数据挖掘与信息共享教育部重点实验室,福建 福州 350002;3. 福州大学 数字中国研究院,福建 福州 350002)
道路边界、实线型标线和铁轨等带状地物,在空间形态上呈显著线性分布特征,其所提供的矢量和结构信息是高精地图、三维导航和基础地理数据库等应用的重要基础数据[1].车载激光雷达系统集成了激光扫描仪、电荷耦合器件(CCD) 相机、全球定位系统(GPS)、惯性导航系统(INS)等多个传感器,能够快速获取带状地物高精度的三维坐标信息[2-3],为带状地物的识别提供了一种新的数据源.
当前基于车载激光点云带状地物的相关研究主要集中于带状地物的提取,通过逐点分析或将三维点云数据投影到二维特征图像上[4],分析不同地物的空间分布特征和几何特征,利用阈值滤波[5-6]、k均值(k-means)聚类[7-8]或SVM等分类器[9]提取带状地物.这些方法提取的结果仍是离散无拓扑的点集,缺乏对带状地物矢量与结构信息的描述.为了获取带状地物矢量化数据,许多学者通过提取带状地物候选点,利用随机采样一致性(RANSAC)[10]、贝塞尔曲线(Bézier)[11-12]、LSD直线检测算法[13]跟踪等方法拟合带状地物.这类方法需要人工定义大量的跟踪准则,才能将离散带状地物点连接成连续的边界线,多适用于直线分布带状地物.Kass等[14]提出的Snake模型具有“高度可变形”特征,克服了对目标矢量化形状的局限性,在目标分割、跟踪与轮廓提取等领域得到广泛应用[15-18].韩婷等[19]提出一种公开地图(OSM)辅助的车载激光点云道路三维矢量边界提取的方法,该方法改进Ribbon Snake模型[20],以梯度矢量流加上宽度约束作为外部能量,提取道路边界线,然后将OSM的先验知识赋给提取的矢量边界线,最终生成具有语义和拓扑信息的矢量道路数据.此类方法解决了因遮挡与数据缺失造成的带状地物提取不完整或漏提取的问题,但其只关注于道路边界的矢量化信息,未能提取道路结构属性信息.
虽然国内外对车载激光点云带状地物矢量化与结构信息提取的研究取得了一定的进展,但仍存在以下问题:1) 针对多形态的带状地物,难以用单一规则语义信息进行跟踪矢量化;2) 目前,带状地物矢量化信息少,缺少对带状地物结构属性信息的提取.为此,本文利用Ribbon Snake模型能将初始估计、几何特征与高层知识约束一起嵌入目标轮廓搜索中的优势[20],提出一种采用车载激光雷达的带状地物矢量化与结构特征提取算法.
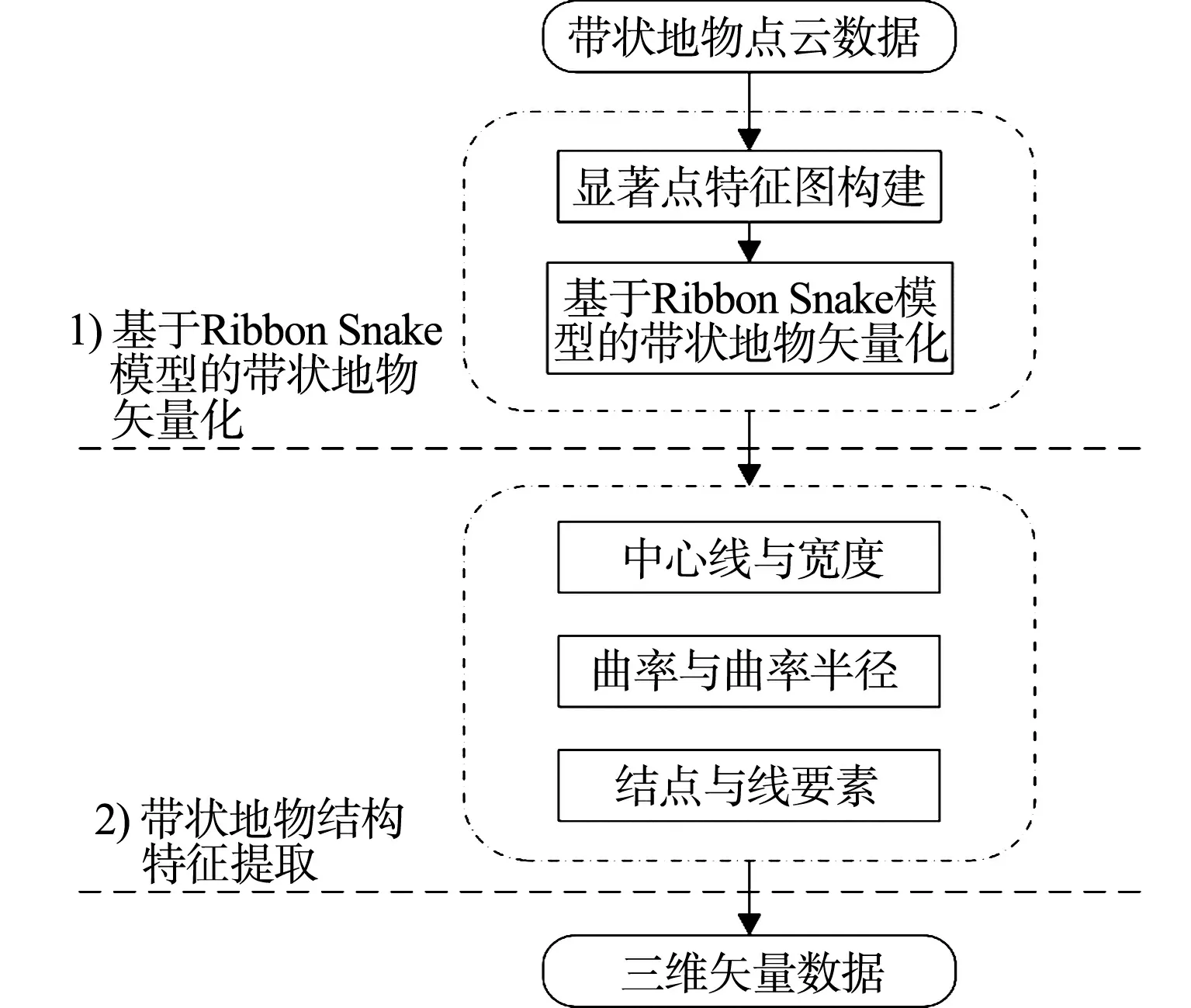
图1 文中算法流程图Fig.1 Algorithm flow chart of this paper
1 带状地物矢量化与结构特征提取算法
文中算法流程图,如图1所示,主要包括以下两个部分.
1) 基于Ribbon Snake模型的带状地物矢量化.利用预先获取的显著带状地物点云数据,构建显著点特征图,然后,采用Ribbon Snake模型提取带状地物矢量化信息.
2) 带状地物结构特征提取.基于带状地物的矢量信息,分场景提取包括中心线与宽度、曲率与曲率半径、结点与线要素等结构信息,实现对带状地物结构语义描述,生成具有几何与结构信息的三维矢量数据.
2 基于Ribbon Snake模型的带状地物矢量化
Ribbon Snake模型可用于提取具有严格对称宽度的带状地物.考虑带状地物的分布并不能保证其两条边界关于中心轮廓严格对称,因此,设计左右宽度可变的Ribbon Snake模型.在显著点特征图上,利用Ribbon Snake实现带状地物矢量化提取.
2.1 显著点特征图构建
对于带状地物点云数据,需要通过格网剖分将点云投影到二维特征图上.具体做法是确定带状地物点x和y的最小坐标(Xmin,Ymin),然后,逐点计算各点云在格网中的行列号i,j,即
(1)
式(1)中:GSD是格网剖分尺寸,即图像的分辨率,可以根据点云密度或扫描仪的分辨率进行确定,当GSD取值越大,地物细节信息丢失越多;反之,保留信息越多.通过判断每个格网内是否存在地物点确定每个格网的灰度值,将存在点的格网赋值为0,其余为255,生成显著点特征图I.
2.2 带状地物矢量化
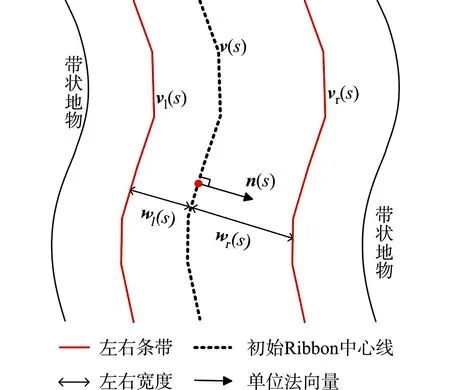
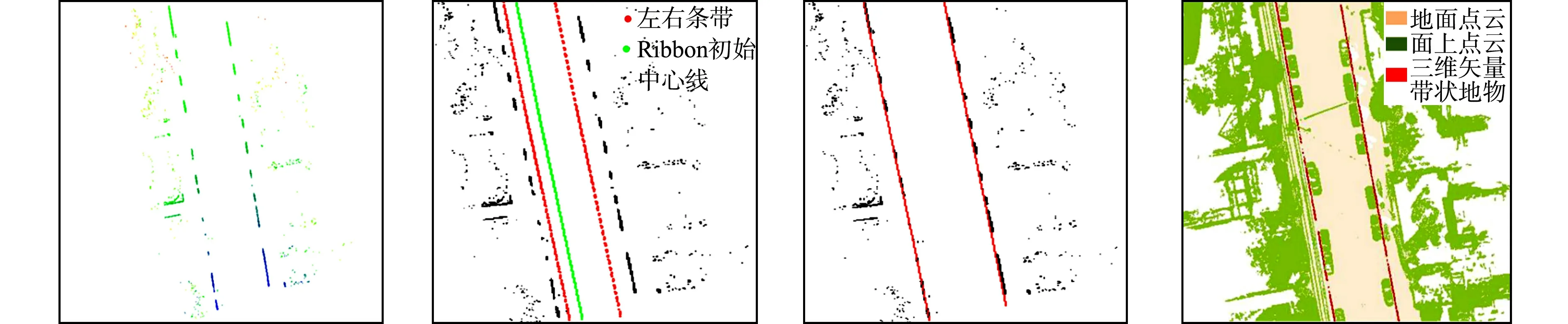
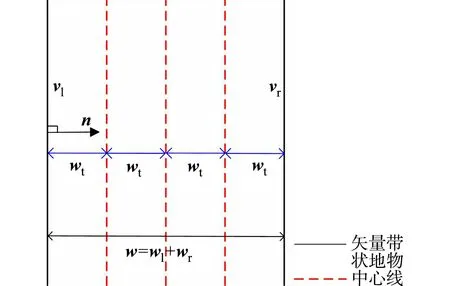
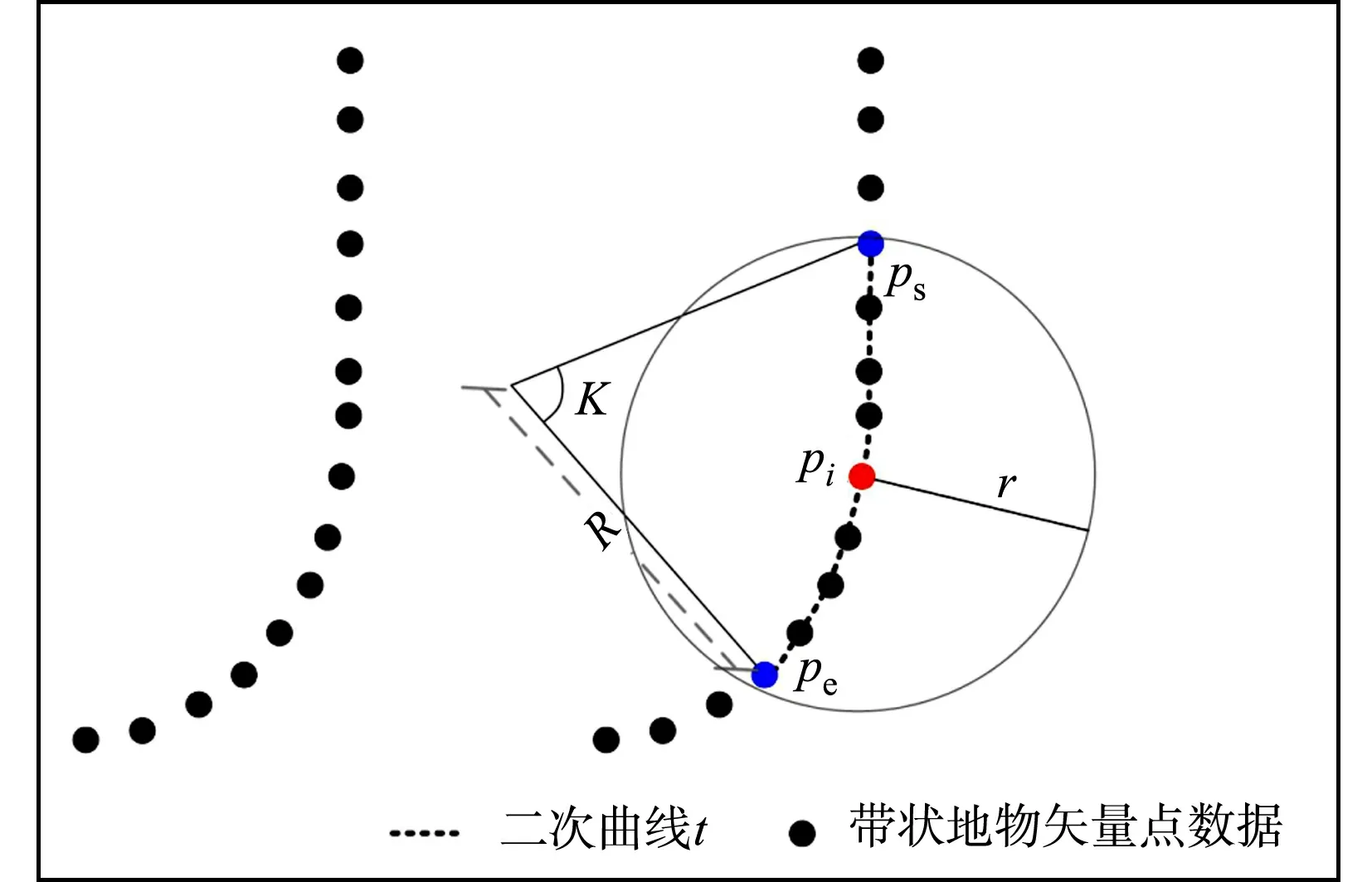
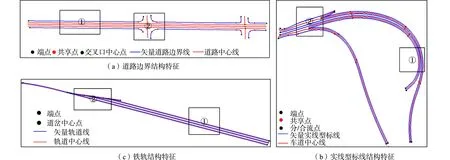
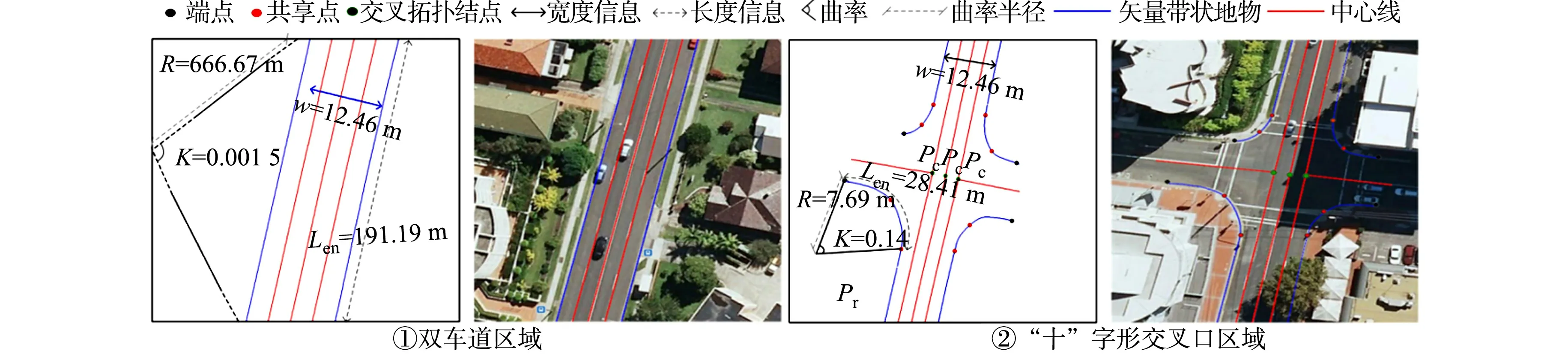
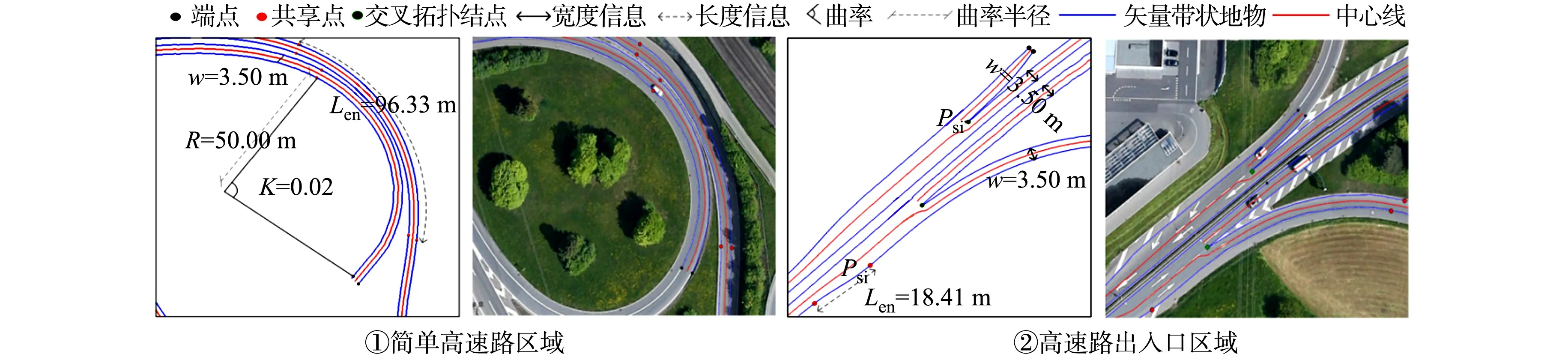
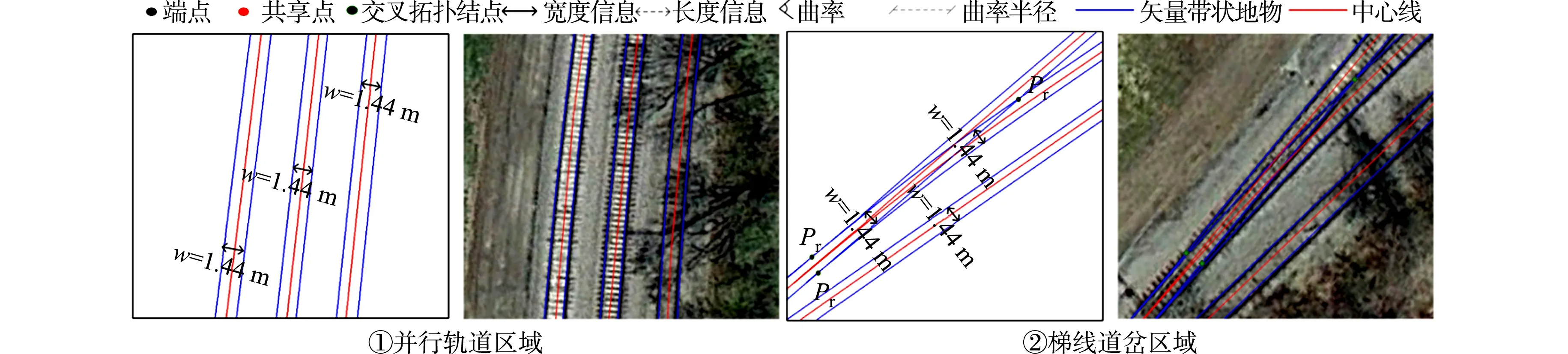
带状地物具有以左、右边界约束车辆行驶区域的特性,可利用轨迹点数据作为Ribbon Snake模型初始位置;若无轨迹点数据,可采用路网矢量数据[21]或众源数据OSM[19]进行初始化.Ribbon Snake模型的初始中心线用参数表示为v(s)=(x(s),y(s),z(s)),0 vl(s)=v(s)-wl(s)·n(s),vr(s)=v(s)+wr(s)·n(s). (2) 图2 Ribbon Snake模型参数化表示Fig.2 Parametric representation of Ribbon Snake model 式(2)中:Eint为内部能量,与传统Snake的定义相似,表示为 (3) Eext为外部能量,用于吸引Snake往目标轮廓处演变,使用图像梯度信息定义Ribbon Snake外部能量,表达式为 Eext=ω(s)(I(vl(s))-I(vr(s)))·n(s). (4) 式(4)中:ω为权重参数;I表示图像的梯度. Ewid为宽度约束能量,是wl(s)和wr(s)的一阶导数,表示为 (5) 式(5)中:λ为权重参数. Ribbon Snake模型将轮廓线逼近目标轮廓的过程转化为求解能量E(v,w)的最小化问题.为了不断优化Snake中各点位置与对应的宽度,利用变分算法将E(v,w)能量泛函最小化[14],通过迭代步长γ和时间t分别求解x(s),y(s),wl(s),wr(s),在能量函数达到最小时,Ribbon Snake收敛于带状地物. 为了获得三维矢量信息,根据Ribbon Snake原理,组成轮廓线的各控制点在能量函数约束下不断优化到带状地物时,虽然位置发生变化,但最终轮廓线控制点顺序与初始化时保持一致[19].因此,只需要将最终的控制点所对应的图像坐标转换为真实坐标,并将对应顺序轨迹点z值赋给控制点,按照顺序连接,则实现带状地物矢量化提取.基于Ribbon Snake模型的带状地物矢量化,如图3所示. (a) 带状地物点云数据(高程赋色) (b) 显著点云特征图与初始化 (c) 基于Ribbon Snake提取矢量带状地物 (d) 带状地物与点云叠加显示图3 基于Ribbon Snake模型的带状地物矢量化Fig.3 Vectorization of strip objects based on Ribbon Snake model 基于Ribbon Snake模型矢量化的带状地物仅包含空间位置信息,为了更详细地描述带状地物的空间结构与几何分布等信息,需进一步提取地物的结构特征.在实际场景中,带状地物类别不同,提供的结构信息也存在差异.因此,分场景(单车道、多车道、道路交叉口、高速路出入口、铁轨道岔口等)构建带状地物的结构特征,具体包括以下结构信息:中心线与宽度、曲率与曲率半径、结点与线要素. 中心线是带状地物几何设计中的重要特征线,结合宽度信息可以提供许多结构信息.利用节2.2中的Ribbon Snake模型,当能量函数达到最小值时,可提取带状地物的宽度信息w=wl+wr.一般而言,根据道路的宽度信息,可以进一步将道路划分为快速路、主干路、次干路和支路4个等级,利用各道路等级对应机动车道标准宽度提取中心线(图4),伪代码如算法1所示.图4中:40≤w≤70;wt=3.75;车道数m=2. 图4 中心线与宽度Fig.4 Center line and width 算法1:中心线提取 输入:宽度信息w,左矢量带状地物vl,右矢量带状地物vr 输出:中心线 if 40≤w≤70 机动车道宽度wt=3.75,计算车道数m=int(w/wt) else 机动车道宽度wt=3.50,计算车道数m=int(w/wt) end 计算单位法向量n ifm等于1 单车道场景;根据公式:中心线=vl+wt·n或中心线=vr-wt·n,求解中心线 else 多车道场景;根据公式:中心线=vl+wt·n或中心线=vr-wt·n,循环求解2m-1条中心线 end return中心线 曲率K与曲率半径R是衡量地物弯曲程度的参数,可作为一种几何特征,引入带状地物结构描述中[22].基于Ribbon Snake模型提取带状地物,首先,逐点pi=vi{xi,yi},i={1,2,…,n}获取局部邻域r内的点集pt={xt,yt},t={1,2,…,m};然后,选用点集内距离最远的两个点ps,pe与该点pi求解二次曲线t的参数(a1,a2,a3),(b1,b2,b3),并将参数代入曲率计算式(7)中,获得该点pi的曲率值K为 图5 曲率与曲率半径Fig.5 Curvature and radius of curvature (6) (7) 曲率半径R为曲率的倒数(图5),表达式为 R=1/K. (8) 在地理信息系统(GIS)中,一般使用结点与线要素对数据进行抽象[23],用以提供重要的几何和拓扑结构.结点要素一般表征特殊位置点或关键拓扑点信息,线要素辅助结点要素,用以确定地物具体形状.因此,也可以通过提取结点与线要素对带状地物结构进行描述[1].据此,分析不同场景中带状地物的空间分布形态,提取相对应结点与线要素,其中,结点要素根据作用的不同划分为位置信息结点(端点与共享点)、交叉拓扑结点(交叉口中心点、分/合流点及道岔中心点). 3.3.1 预处理 在实际场景中,带状地物存在直线与曲线两种分布形态,为了使所提取的结点与线要素更准确地描述其分布形态,需依据节3.2提取的曲率大小,采用k-means聚类算法对带状地物进行二分类(图6(a)).由于提取交叉拓扑结点时,需要辅助线要素进行判别,因此,首先对线要素进行提取,再提取结点要素. 3.3.2 线要素提取 在用线要素描述带状地物结构特征时,可以使用其形态与长度信息.基于分类结果,已获得线要素形态信息,若各线段由m个点组成,则各线段的长度Len为 (9) 线要素表示方式为La_b,其中,a取l或r时分别表示该线段为左或右带状地物;b表示线段编号,按顺序进行取值.线要素,如图6(b)所示. 3.3.3 结点要素提取 1) 位置信息结点.基于分类结果,定义直线与曲线型带状地物位置信息结点提取规则:对于直线型带状地物,使用始末点进行抽象;对于曲线型带状地物,使用始末点和中间结点进行抽象.位置信息结点表示为Sa_b,Ca_b,Ea_b,其中,S,C,E分别表示起始点、中间结点与终止点(图6(c)). 为了保证带状地物线段与线段之间的连续性,确定各线段之间的关联关系,需进一步将提取的位置信息结点划分为端点与共享点.其中,共享点是描述具有关联关系的线要素之间的结点[24],剩余位置信息结点为端点.因文中使用Ribbon Snake模型矢量化带状地物可以同步确定点的顺序关系,基于此,通过判断线段La_b始末点之间的连续性,即a的一致性与b的顺序性,确定连接两线段的共享点(Ja_b),其中,b值取所关联的两线段编号(图6(d)). (a) 带状地物分类点数据 (b) 线要素 (c) 位置信息结点要素 (d) 位置信息结点要素与线要素图6 结点与线要素Fig.6 Node and line elements 2) 交叉拓扑结点.交叉拓扑结点是记录带状地物空间分布中具有关键拓扑信息的点,一般位于带状地物相交处,据此求解交叉拓扑结点伪代码,如算法2所示. 算法2:交叉拓扑结点提取 输入:矢量带状地物L={La_1,…,La_N},N为带状地物条数,a=l为左带状地物,a=r为右带状地物 输出:交叉拓扑结点Pk,k={c,si,r} fori=1∶N 计算Li={Pi,1,…,Pi,end}与Lj={Pj,1, …,Pj,end},j≠i,j∈(1,N)内,Pi,k(k为Li点数)与Pj,h(h为Lj点数)之间 的距离值d ifd≤do(do为接近于0的值,根据实际 场景确定) Pk取min(d)对应两点中间坐标 break else continue end end returnPk 根据场景的不同,交叉拓扑结点Pk发挥的作用各不相同.交叉拓扑结点类型,如表1所示. 针对交叉口场景,交叉口中心点位于两条或两条以上中心线相交处,是描述交叉口的一个重要结构信息,用于辅助管理交通运行.利用算法2提取交叉口中心点Pc时,以中心线作为输入L,提取结果如图7(a)所示.针对高速路出入口场景,分/合流点是引导车辆分道或并道行驶的重要拓扑点,在根据算法2提取分/合流点Psi时,取左、右带状地物L进行两两组合计算交点(图7(b)).针对铁路轨道场景,道岔是机动车辆从一股轨道转入或越过另一股轨道时必不可少的线路设备,是铁路轨道的一个重要组成部分.在对铁路轨道结构进行描述时,各铁轨交叉聚合分离处的道岔中心点是必不可少的结构信息之一.道岔在实际场景中存在多种分布形态,结合算法2提取的道岔中心点Pr,如图7(c)所示. 表1 交叉拓扑结点类型Tab.1 Cross topology node type (a) 交叉口中心点 (b) 分/合流点 (c) 道岔中心点图7 交叉拓扑结点Fig.7 Cross topology node 为了验证文中方法的有效性,选取3份经过预处理提取的显著带状地物点云数据[7,9,12]进行实验.实验数据,如图8所示.图8中:3份数据均存在因遮挡或数据缺失造成的断裂和噪声点问题,其中,数据1是从长约420 m城市街道场景提取的道路边界点,其主要特点是数据密度较大,以多车道与道路交叉口场景为主;数据2是从长约480 m的高速公路场景提取的实线型标线点,场景复杂,存在大量曲线型实线型标线;数据3是从长约420 m的铁路场景提取的轨道点,多条铁轨交叉聚合分离,远离铁路环境中的数据点密度稀疏. 构建特征图的格网剖分尺寸GSD可根据激光扫描仪分辨率确定,设为0.2.Ribbon Snake模型涉及的权重参数为α,β,ω,λ,通过选取直线型和曲线型两份实验数据(图9),设计5组实验方案(表2)进行确定.表2中:α+β=1,ω+λ=1,在固定ω和λ均为0.5的情况下,α与β分别取0.1,0.5,0.9,找到效果最佳的α与β参数组合.在此基础上,分别选取ω和λ为0.1,0.5,0.9,确定效果最佳的ω和λ.为了更好地对比不同方案的实验效果,选取迭代100次时Snake收敛的中间结果(图9(a)~(e))进行分析. (a) 数据1 (b) 数据2 (c) 数据3图8 显著带状地物点云数据Fig.8 Salient strip object point cloud datas (a) 方案1(直线) (b) 方案2(直线) (c) 方案3(直线) (d) 方案4(直线) (e) 方案5(直线) (f) 方案1(曲线) (g) 方案2(曲线) (h) 方案3(曲线) (i) 方案4(曲线) (j) 方案5(曲线)图9 5组实验方案的直线型和曲线型实验数据Fig.9 Linear and curvilinear experimental data of 5 experimental schemes 表2 实验方案参数设置Tab.2 Experimental scheme parameter setting 内部能量参数α和β控制Snake曲线的连续性和平滑性,对比实验方案1,2,3可知:当α为0.1时,Snake曲线光滑性差;α为0.5时,在数据缺失区域收敛不佳;α为0.9时,曲线相对平滑,在数据缺失区域收敛效果较好.因此,考虑实验数据存在数据缺失的情况,为保证Snake的连续性与平滑性,将α与β分别设为0.9,0.1.固定内部能量权重参数,对比实验方案2,4,5可知:将外部能量权重ω设为0.5时,Snake抖动明显,收敛效果不佳;当ω为0.1时,Snake曲线相对平滑,但运动缓慢,运行效率低;当ω为0.9时,两份数据基本收敛且曲线相对平滑.据此,综合考虑收敛效果与运行效率,将ω设为0.9,λ设为0.1,迭代步长γ与局部搜索邻域半径r均设置为0.5. 基于以上研究方法,采用表3的实验参数设置,实现3份实验数据带状地物的矢量信息提取,如图10所示. 表3 实验参数设置Tab.3 Experimental parameter settings 由图10可知:3份实验数据中,绝大部分带状地物均能被较好地拟合,不仅能有效拟合直线型带状地物(图10(c)),且对曲线型带状地物也有较好的收敛效果(图10(b)),同时,适用于因遮挡造成不连续的带状地物的优化(图10(a)).但在道路交叉路口和高速路出入口,在两条Ribbon Snake矢量的道路边界出现误提取(图10(a)②,图10(b)②),需进一步进行优化.逐条逐点遍历Snake点,删除位于无显著特征点(即格网值为255)处的Snake点;然后,根据Snake的连续性组合带状地物,得到优化结果.误提取和优化后的矢量带状地物,如图11所示. (a) 数据1 (b) 数据2 (c) 数据3图10 带状地物矢量信息提取结果Fig.10 Vectorization information extraction results of strip objects (a) 道路交叉口误提取与优化后的矢量带状地物 (b) 高速路出入口误提取与优化后的带状地物图11 误提取和优化后的矢量带状地物Fig.11 Vector strip objects after error extraction and optimization 为了更详细地描述带状地物,通过分析Ribbon Snake提供的宽度与矢量边界信息,进一步提取其结构信息.带状地物结构特征提取结果,如图12所示.为了更加直观地对比带状地物结构特征提取结果与实际场景的吻合度,将实验数据中6个子图的三维矢量数据转换成锁眼标记语言(keyhole markup language,KML)文件,将其加载至Google Earth进行叠加显示,如图13所示. 图12 带状地物结构特征提取结果Fig.12 Structural feature extraction results of strip objects (a) 道路边界结构特征 (b) 实线型标线结构特征 (c) 铁轨结构特征图13 带状地物结构特征提取结果(分场景)Fig.13 Structural feature extraction resultsof strip objects (scene by scene) 由图13可知:带状地物结构特征提取的结点和线要素能够与实际环境较好地吻合.3份实验数据结构特征的结点与线要素信息,如表4所示.表4中:端点是组成带状地物线要素始末位置点;共享点是连接具有拓扑关联要素的结点,该点的移动或修改不会影响线要素之间的关联关系.交叉口中心点(图13(a)②)、分/合流点(图13(b)②)、道岔中心点(13(c)②)与实际场景匹配地较好.分析Ribbon Snake模型提供的宽度信息,可以区分实际场景车道级别,在矢量边界信息基础上,实现多条中心线(图13(a)①)的提取.在高速路场景(图13(b)①),通过结构特征分析,确定该场景宽度规范,补全缺失的中心线与边界.铁轨分布形态与单车道场景类似,利用轨道宽度信息,生成各轨道中心线(图13(c)).曲率与曲率半径可以获取道路、铁轨等场景下带状地物的弯曲情况,当曲率接近于0时,带状地物呈现直线分布形态(图13(a)①);反之,多为曲线分布(图13(b)①).针对交叉口场景(图13(a)②)),结合提取的交叉中心点与曲率信息,可用于推演该路口车辆转弯半径与行驶车速等信息. 表4 带状地物结点与线要素信息表Tab.4 Node and line element information table of strip objects 综上所述,基于Snake提取的矢量边界与宽度信息,可以提取包括中心线与宽度、曲率与曲率半径、结点与线要素等结构信息,实现不同场景下带状地物的有效完整描述.为进一步验证方法的有效性,与Cloud Compare软件交互提取的带状地物作为参考数据,统计实验结果中正确提取的带状地物总长度(TP)、错误提取的带状地物总长度(FP)、缺失的带状地物总长度(FN),计算正确度(ηcor)、完整度(ηcom)和总体精度(ηQ),并对提取结果进行分析;同时,对图13中3份数据选取的2个场景进行宽度比较.矢量带状地物的提取精度和宽度差值对比,如表5,6所示. 表5 矢量带状地物的提取精度Tab.5 Precision of vector strip objects extraction 表6 矢量带状地物的宽度差值对比Tab.6 Contrast of the width difference of vector strip objects m 由表5,6可知:与数据1,2相比,数据3中带状地物矢量提取的正确度与完整度最高,且宽度与实际场景偏差最小,效果最佳,这是因为该数据带状地物形状相对比较规则,边界较完整,且具有规范的宽度约束;数据2因存在多处车辆交汇复杂场景,总体精度较低;受场景复杂与点密度不均的影响,3份数据场景②的宽度偏差较大.整体而言,3份实验数据提取结果的正确度达到 98.26%以上,完整度达到 98.36%以上,总体精度达到96.68%以上,基于矢量信息提取的结构与软件交互的结果也有较好的吻合度,最大偏差均不超0.004 7 m,表明文中方法能准确地提取绝大多数带状地物的矢量与结构信息. Ribbon Snake模型具有“高度可变形”特征,克服了对带状地物形状的局限性.提出一种基于Ribbon Snake模型的带状地物矢量化与结构特征提取方法,不仅适用于道路边界,对实线型标线与铁轨也有较好的提取效果,实现了包括直线型与曲线型带状地物的矢量化提取;同时,基于带状地物的矢量信息提取不同道路和铁路场景下带状地物的结构特征,最终生成具有准确几何和结构的三维矢量数据.但由于缺乏箭头标线等指示性数据,使所提取带状地物三维矢量数据缺乏方向等属性,因此,未来的一个工作方向是完善带状地物的结构信息的提取.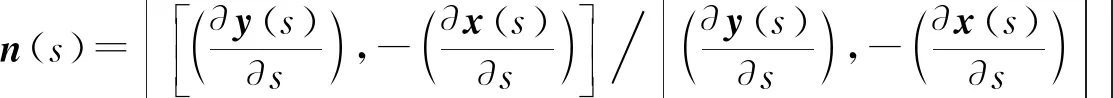

3 带状地物结构特征提取
3.1 中心线与宽度
3.2 曲率与曲率半径
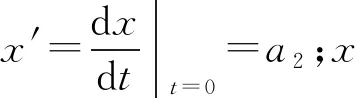
3.3 结点与线要素
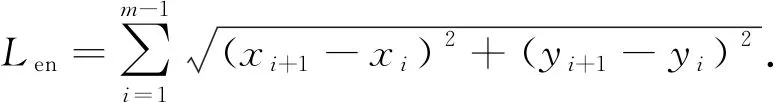





4 实验分析
4.1 实验数据与参数
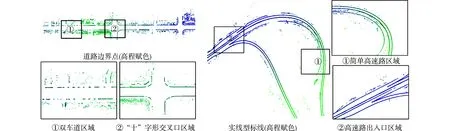


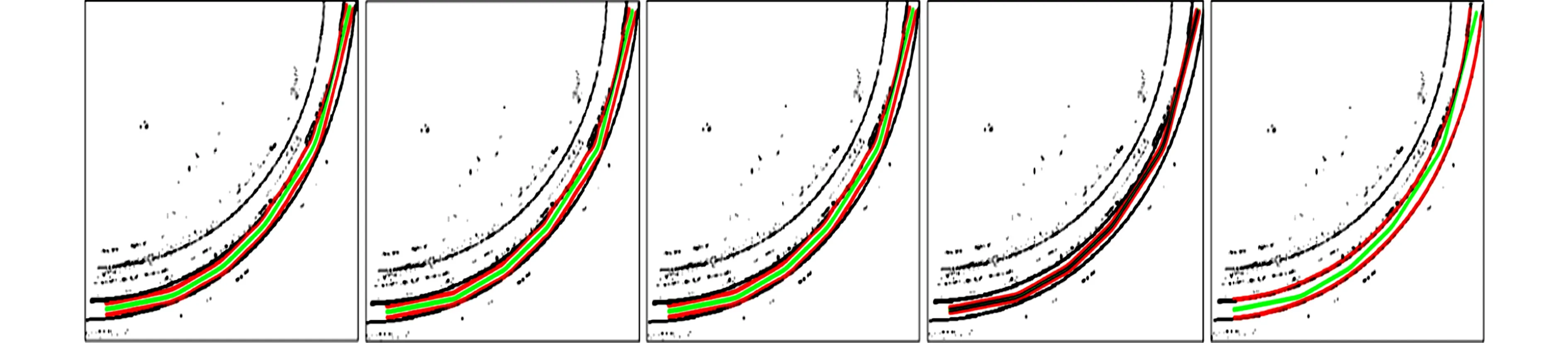
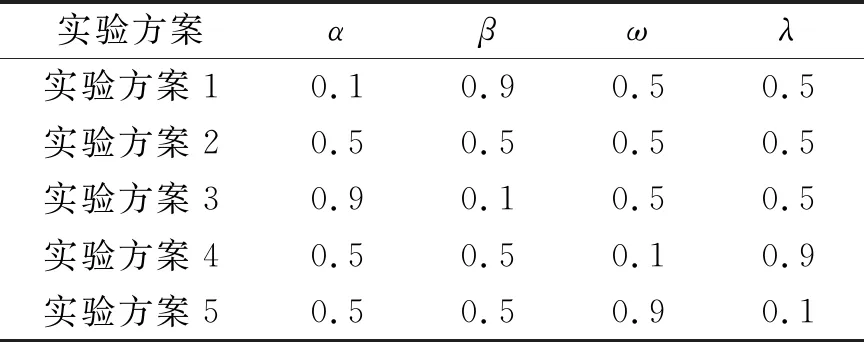
4.2 实验结果及分析

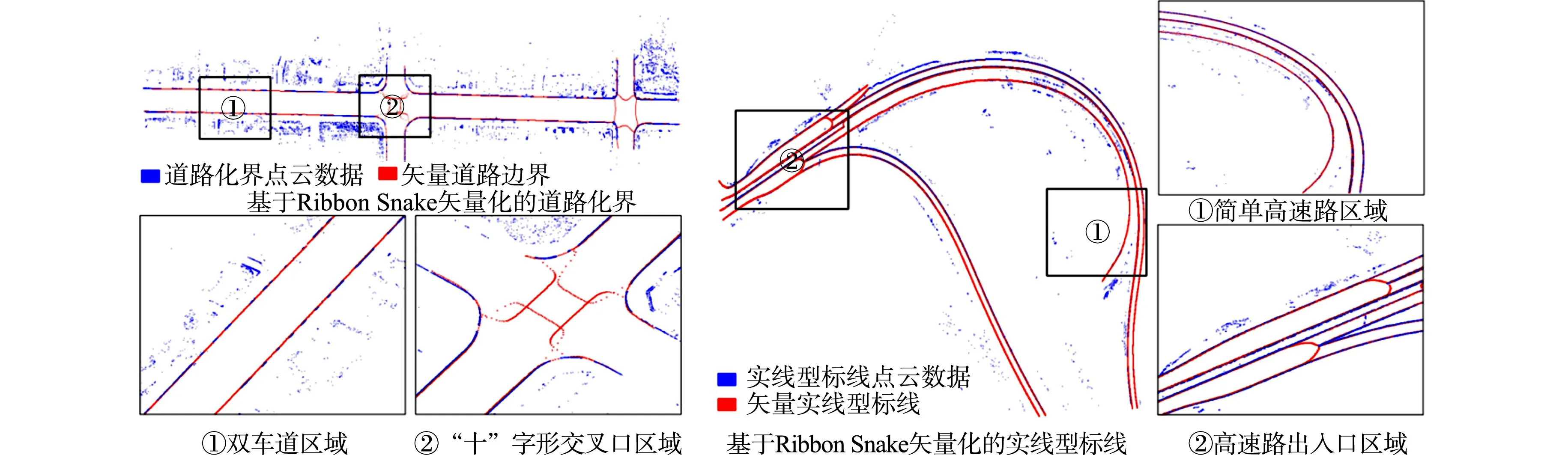





5 结束语
——目镜套筒

