寒冷地区空气冷却型PV/T系统性能模拟分析

罗成，张媛媛，秦智胜，邹鹏，程远达

(太原理工大学 土木工程学院，山西 太原 030024)

太阳能光伏电池的研究和实际应用中的各种数据表明，光伏电池温度每升高1 ℃，光电转换效率下降约0.45%[1].为提高光伏电池的能源转换效率，学者们提出一种集光伏发电与光热利用为一体的太阳能光伏光热(PV/T)系统[2].根据冷却介质的不同,PV/T系统可分为空气冷却、水冷却、制冷剂冷却、纳米流体冷却[3-6]等类型.相较于其他冷却形式，空气冷却型PV/T系统具有以下3个优势：1) 冷源方便获取，无成本；2) 无需考虑液体冷凝膨胀、管道腐蚀现象；3) 装置轻巧、安装方便、成本较低.因此，空气冷却型PV/T系统得到较为广泛的关注和研究.

Hegazy[7]分析单侧空气通道(光伏板上、下)和双侧通道(通道不连通、连通)4种不同结构形式的空气冷却型PV/T系统的性能，结果表明,双侧通道不连通的PV/T系统的性能优于其他3种结构形式.Shan等[8]也对这4种结构形式的空气冷却型PV/T系统进行理论计算，结果表明，仅仅通过改变空气冷却型PV/T系统结构来实现系统热效率和光电转换效率的增加较为困难.王婷[9]对空气通道分别位于电池板的上侧和下侧的PV/T系统进行模拟研究，结果表明，如果PV/T系统更看重能量的品质，或更偏向于电能的输出，则应具体问题具体分析.Joshi等[10]研究印度地区冬季空气冷却型PV/T系统一天内不同时刻的效率变化情况，发现光伏余热的利用使系统效率增加约2%～3%.Yazdanpanahi等[11]从热力学第二定律角度对PV/T系统效率的计算进行修正，提出从损失方向计算系统效率更为准确.目前,大多数文献侧重于研究辐照强度、环境温度与环境风速等环境参数,以及空气入口流速和温度等流体状态参数对空气冷却型PV/T系统性能的影响.然而，各个地区的环境因素不尽相同，具有各自的特点，且系统性能受这些因素的综合影响，不具有普遍适用性.此外，冷却通道长度和高度等结构参数对系统性能也有重要的影响，在前期设计时需尤为关注，但对这方面的研究目前仍然较少，有待进一步加强.为了提高太阳能利用效率，本文结合太原地区夏季典型日的气象参数，对冷却通道位于光伏板上侧的空气冷却型PV/T系统进行研究，分析冷却通道长度、高度及空气入口流速等设计参数对系统性能的影响.

1 物理及数学模型

冷却通道位于光伏板上侧的空气冷却型PV/T系统(简称文中PV/T系统)的物理模型，如图1所示.图1中：L，H，W分别表示空气冷却通道的长度、高度和宽度.

图1 文中PV/T系统的物理模型Fig.1 Physical model of PV/T system in paper

为简化计算模型，提出以下5点假设.

1) 系统中各表面均为漫灰表面，且不考虑系统底面和侧面的热损失.

2) 空气不参与辐射换热，空气的密度设定中开启Bossinesq假设.

3) 不考虑玻璃盖板及光伏电池板表面灰尘及污垢对采光的影响.

4) 空气流动为稳态湍流情形.

5) 光伏组件水平放置，以吸收水平面上的太阳辐射总强度.

文中PV/T系统采用的光伏组件和玻璃盖板的物性参数如下：玻璃盖板厚度δg为0.005 m；玻璃盖板的热导率λg为0.74 W·(m·K)-1；玻璃盖板的吸收率αg为0.05；玻璃盖板的穿透率τg为0.91；光伏组件的热导率λc为0.647 W·(m·K)-1；光伏组件的吸收率αc为0.80；光伏组件的发射率εc为0.90.

数值模拟计算采用Fluent 15.0软件，计算域包括玻璃盖板、光伏组件及整个通道内的空气区域，选用标准k-ω湍流模型计算冷却通道内部的流动和换热情形[12]，控制方程具体如下.

连续性方程为

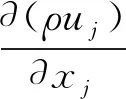
(1)

动量方程为

(2)

能量方程为

(3)

湍流动能k方程为

(4)

湍流耗散率ω方程为

(5)

式(1)～(5)中：ui，uj，uk分别为i，j，k方向的速度,m·s-1;xi，xj，xk为坐标分量;T为为流体温度，K;σT为Prandtl数;μ,μt为湍流粘度,Pa·s；λ为导热系数，W·(m·K)-1;ρ为密度,kg·m-3;cp为比热容，J·(kg·K)-1；Gk是由层流速度梯度而产生的湍流动能，kg·(mg-3)-1；Gω为湍流耗散率ω生成项，kg·(m·s3)-1；Γk，Γω分别为k，ω的扩散率；Sk，Sω为用户自定义项；Yk，Yω分别是由紊流引起的k，ω的耗散项，kg·(m·s3)-1.

同时，选用离散坐标(DO)辐射模型对冷却通道内部的辐射换热进行计算，沿S方向传播的辐射方程[13]为

(6)

式(6)中：G为辐射强度，W·m-2，依赖于位置向量r和方向向量s；a为光谱吸收系数；n为折射率；s′为散射方向；σ为斯蒂芬·玻耳兹曼常数，σ=5.67×10-8W·(m2·K4)-1；σs为散射系数；Tamb为环境温度，K；Φ为相位函数；Ω′为空间立体角.

考虑实际条件下光伏电池板自身产生的电能对热流密度的影响，应用用户定义函数(UDF)的初始化功能，以边界条件的形式，把实际情况下光伏电池板面热流密度值加载到光伏电池板表面上.

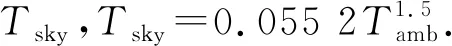
采用绝对速度、分离隐式求解器进行三维稳态计算，采用有限容积法进行方程离散，采用SIMPLE算法进行压力-速度的耦合迭代；动量方程、能量方程、湍流动能k方程、湍流耗散率ω方程均采用二阶迎风格式；连续性方程、湍流动能k方程和湍流耗散率ω方程的残差收敛标准都设置为10-5，能量方程设置为10-6.

2 网格独立性检查与模型验证

采用六面体结构性网格对计算域进行划分.为了检查网格的独立性，分别对网格数为139 664，204 336，304 760，481 481，609 910，702 455的系统进行计算.

在模拟工况中，冷却通道长度L=2.4 m，宽度W=0.45 m，高度H=0.05 m，空气入口流速vin=2.0 m·s-1，空气入口温度Tin=300.8 K，环境温度Tamb=300.8 K，环境风速vw=2 m·s-1，太阳辐射强度固定为G=944.44 W·m-2.

不同网格数下，空气出口流体截面平均温度(Tout，ave)及光伏板平均温度(TPV,ave)，如表1所示.由表1可知：在不同的算例中，模拟结果的计算偏差均小于5%.因此，综合考虑运算时间与计算准确性，使用网格数为481 481的模型进行模拟计算分析.

通过文献[7]的数据对文中建立的数值模型进行验证，文中建立的数值模型尺寸与文献[7]一致，采用的气象参数与文献[7]中每个时刻一致，验证对象为Tout，ave和TPV,ave.Tout，ave和TPV,ave的对比结果，如图2所示.

由图2可知：模拟计算结果与文献[7]中的实验数值吻合较好.经计算可得模拟值与实验值的均方根偏差分别为2.62%和0.88%.因此，文中采用的数值模型具有可靠性.

表1 不同网格数下空气出口流体 截面平均温度及光伏板平均温度Tab.1 Average temperature of air outlet fluid cross section and average temperature of photovoltaic panel under different grid numbers

图2 Tout，ave和TPV,ave的对比结果 Fig.2 Comparison results of Tout，ave and TPV,ave

3 模拟工况设置及系统评价指标

山西省太原地区夏季典型日辐照强度、环境温度及环境风速的逐时变化曲线，如图3所示.图3中：tamb为环境温度,为便于说明，环境温度采用摄氏温度.

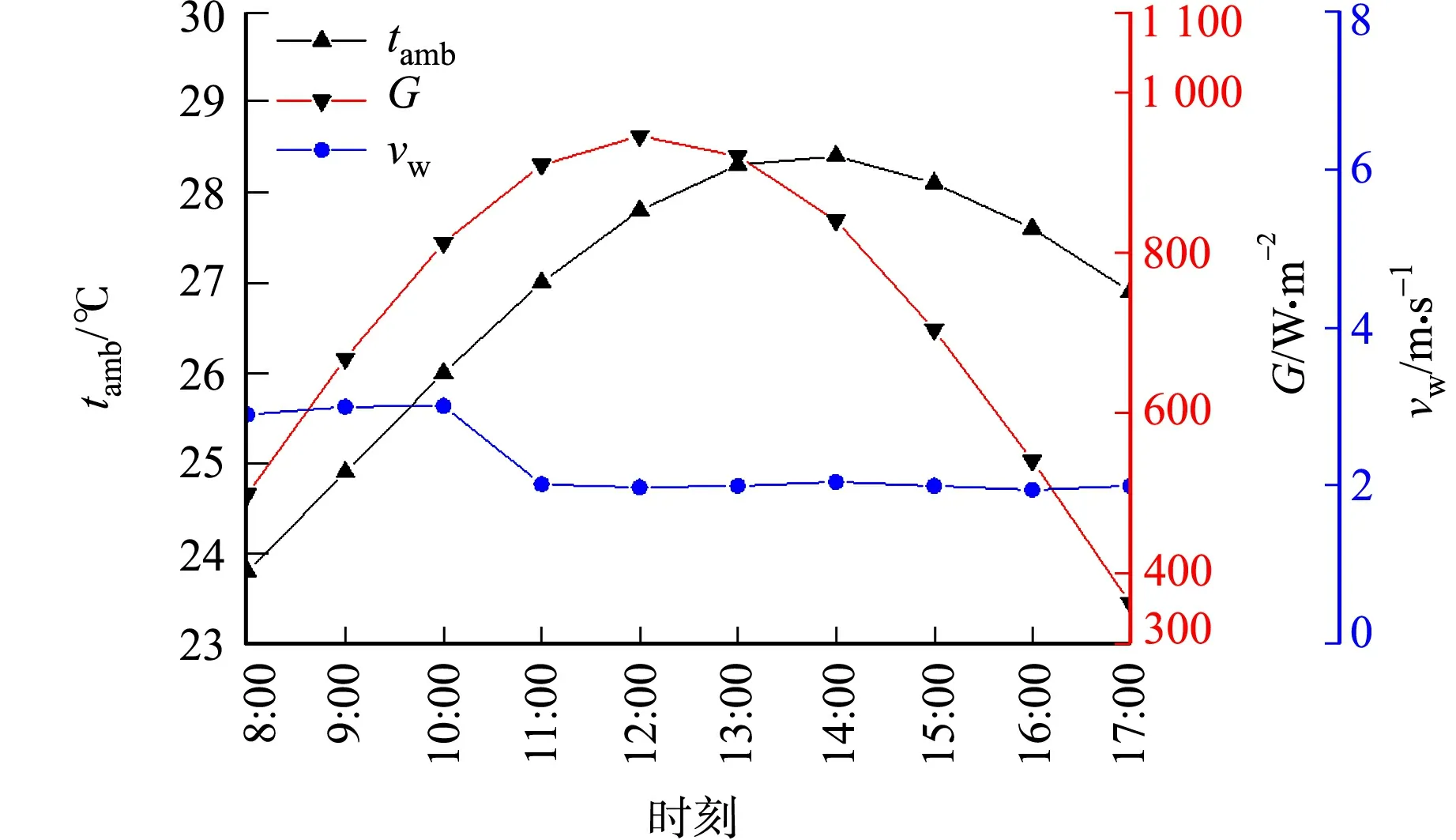
图3 辐照强度、环境温度及环境风速的逐时变化曲线Fig.3 Hourly variation curve of irradiation intensity, environment temperature and environment wind speed

分析不同长度和高度的冷却通道、不同空气入口流速对空冷型PV/T系统性能的影响.研究冷却通道长度对系统性能的影响时，冷却通道长度L设置1.2，1.8，2.4，3.0，3.6，4.2 m等6个变量，冷却通道高度H取0.05 m，空气入口速度取2.0 m·s-1，气象参数取太原地区夏季典型日12:00的气象参数.研究其他变量的工况设置方法与之类似，不再赘述.模拟工况汇总表，如表2所示.

采用热效率、平均电效率和效率作为系统性能的评价指标.

系统的热效率ηth[14]为

(7)

式(7)中：m为空气的质量流量，kg·s-1；Tin为空气入口温度，等于环境温度，K；Ac为光伏电池板的面积,Ac=W·L.

系统的光电转换效率用平均电效率ηe，ave[9]进行描述，即

ηe,ave=ηc[1-0.004 5(TPV,ave-298.15)]×100%.

(8)

式(8)中：ηc为光伏电池板在标准状况下(光伏电池板温度TPV=298.15 K，G=1 000 W·m-2)的光电转换效率，取0.15[15]；光伏电池板的温度系数取0.004 5[1].

表2 模拟工况汇总表Tab.2 Summary table of simulated working conditions

同时，考虑能量的品质，采用净输出计算系统的效率[16].在PV/T系统中，系统的热效率ηex,th与电效率ηex,e,ave分别为

(9)

(10)

式(9)，(10)中：Ts为太阳表面温度，取5 760 K；QF为系统风机所耗电能.

PV/T系统的效率ηex为

ηex=ηex，th+ηex，e，ave.

(11)

4 结果与讨论

4.1 冷却通道长度对系统性能的影响

设定冷却通道宽度W=0.45 m，高度H=0.05 m，空气入口流速vin=2.0 m·s-1，太阳辐照、环境温度及环境风速采用太原地区夏季典型日中午12:00的气象参数，冷却通道长度L分别选取1.2，1.8，2.4，3.0，3.6，4.2 m(工况1),进行模拟研究.系统的热效率、平均电效率及效率随冷却通道长度的变化情况，如图4所示.由图4可得以下3个结论.

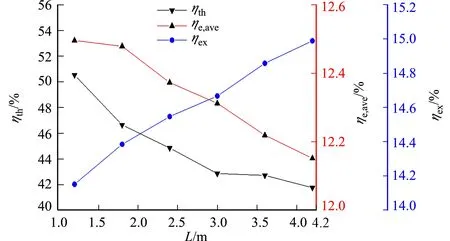
图4 冷却通道长度对系统性能的影响Fig.4 Influence of cooling channel length on system performance

1) 随着冷却通道长度的增加，文中系统的热效率从50.53%逐渐降低到41.75%，这是因为空气沿着冷却通道流动，不断与光伏板进行换热,使温度逐渐上升，导致冷却通道中后段的空气与光伏板之间换热温差逐渐减小，削弱空气对光伏板的冷却效果，所以随着冷却通道长度逐渐增大，其弱化换热的光伏板长度占总长度的比例也逐渐增大，导致系统热效率随着冷却通道长度的增大而逐渐降低.

2) 随着冷却通道长度的增加，系统平均电效率从12.48%逐渐降低到12.15%，这是因为随着冷却通道长度的逐渐增大，其弱化换热的光伏板长度占总长度的比例也逐渐增大，光伏板温度较高的面积比例逐渐增大，导致光伏板的平均温度逐渐增大，系统的平均电效率逐渐降低.

3) 随着冷却通道长度的增加，系统的效率从14.15%逐渐增加到14.99%，这是因为随着冷却通道长度的增大，系统热效率逐渐增大，虽然系统电效率逐渐降低，但较热效率的增大值而言,电效率的降低值较小，二者共同影响下导致系统的效率逐渐增大.

4.2 冷却通道高度对系统性能的影响

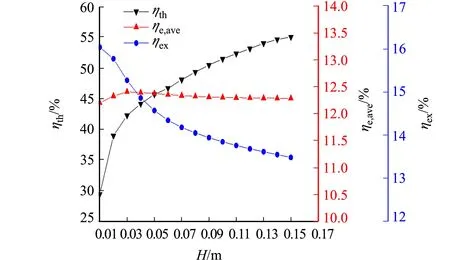
图5 冷却通道高度对系统性能的影响Fig.5 Influence of cooling channel height on system performance

设定冷却通道宽度W=0.45 m，长度L=2.4 m，空气入口流速vin=2.0 m·s-1,太阳辐照、环境温度及环境风速取太原地区夏季典型日中午12:00的气象参数，冷却通道高度H选取0.01～0.15 m(工况2)，进行模拟研究.系统的热效率、平均电效率及效率随冷却通道高度的变化情况，如图5所示.由图5可得以下3个结论.

1) 冷却通道高度从0.01 m增加到0.15 m，系统热效率从29.39%增加到54.95%，这是因为随着冷却通道高度的逐渐增大，参与换热的冷却气体总量逐渐增多，冷却空气与光伏板间的换热平均温差逐渐增大，增强空气与光伏板之间的换热程度，导致系统热效率随着冷却通道高度的增加而逐渐提高.

2) 随着冷却通道高度的增加，系统平均电效率先缓慢增大，而后维持不变.这是因为冷却通道高度在较小范围内增长时，空气与光伏板之间的平均换热温差显著增大，且显著增强空气对光伏板的冷却效果，光伏板的温度降低，系统平均电效率逐渐升高;随着冷却通道高度进一步增大，空气与光伏板之间换热温差的增大对高度变化的影响逐渐降低，虽然换热量逐渐增大，但光伏板平均温度却基本维持不变.

3) 当冷却通道高度从0.01 m增加到0.15 m，系统效率从16.04%降低到13.48%，随着冷却通道高度的增加，空气总热量虽然增多，但空气出口截面平均温度却逐渐减小，使系统热效率逐渐减小，而平均电效率基本维持不变，风机耗电量却逐渐增加，因此，电效率与效率逐渐减小.

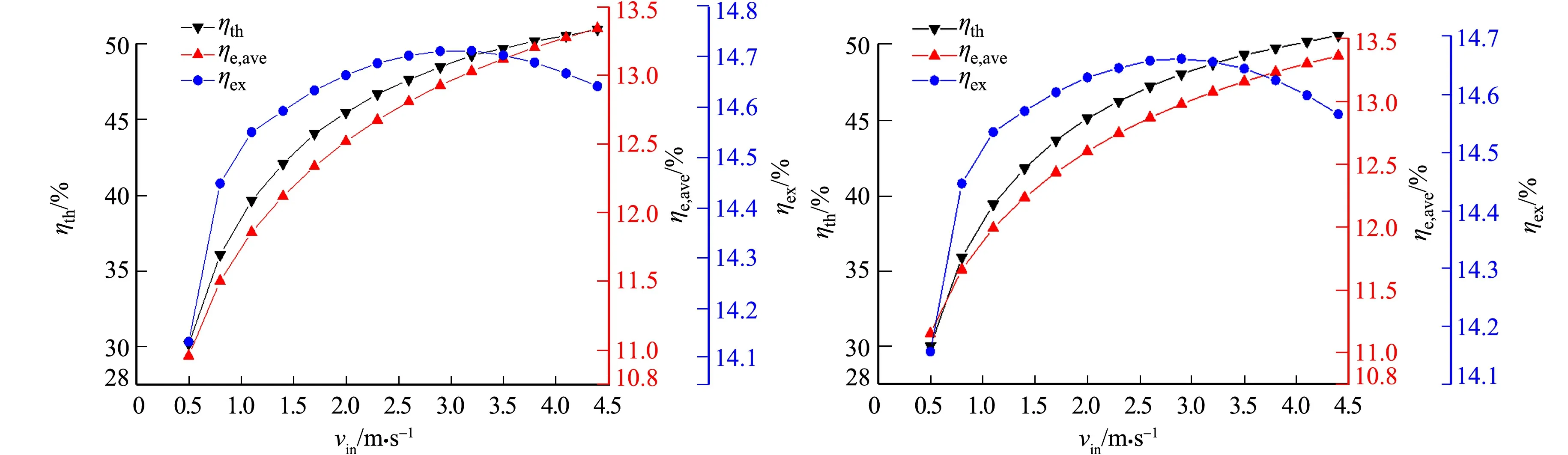
(a) 11:00 (b) 14:00 图7 不同空气入口流速对系统性能的影响Fig.7 Influence of different air inlet velocity on system performance

4.3 不同时刻下空气入口流速对系统性能的影响

设定冷却通道宽度W=0.45 m，长度L=2.4 m，高度H=0.05 m，空气入口流速取工况3中的数值，气象参数取太原地区夏季典型日8:00-17:00的太阳辐照、环境温度及环境风速.各时刻最佳运行工况及最优效率，如图6所示.由图6可知：最佳空气流速范围为0.8～3.2 m·s-1，对应的系统效率变化范围为14.61%～15.24%.以11:00和14:00为例,说明空气入口流速对系统性能的影响，如图7所示.由图6，7可得以下3个结论.

1) 随着空气入口流速的增大，系统热效率逐渐升高，这是因为随着空气入口流速的逐渐增大，空气的紊流程度逐渐增大，空气与光伏板之间的换热程度增强.

2) 随着空气入口流速的增大，系统的平均电效率增大，这是因为空气与光伏板之间换热程度逐渐增强，使空气对光伏板具有更优的冷却效果，光伏板平均温度随空气入口流速的增大而逐渐降低，导致系统平均电效率逐渐增大.

3) 随着空气入口流速的增大，系统的效率先增大后减小，且存在极值点使系统效率取得最大值，这是因为当空气入口流速在小范围内增长时，空气总热量虽然增多，但是空气出口截面平均温度却逐渐减小，导致系统热效率逐渐减小，而系统平均电效率却显著增加，导致电效率逐渐增大，且热效率的减小值小于电效率的增大值，所以系统效率先增加，但随着空气入口风速进一步增加，风机耗电也逐渐增大，这部分能量对总效率的变化趋势起主导作用，在诸多因素的共同影响下，导致系统的效率呈现先增大后减小的变化规律.

5 结论

对冷却通道位于光伏板上侧的空气冷却型PV/T系统性能进行模拟研究，得出以下4个结论.

1) 随着冷却通道长度的增加，系统的热效率和平均电效率逐渐降低，效率随着冷却通道长度的增加而逐渐增大.

2) 随着冷却通道高度的增加，系统的热效率逐渐增大，平均电效率先缓慢增大后基本维持不变，效率则逐渐降低.

3) 随着空气入口流速的增大，系统的热效率和平均电效率逐渐增大，效率先增大后减小，且存在极值点使系统效率取得最大值.在寒冷地区夏季典型日工况下，随着气象参数的变化，最佳空气流速范围为0.8～3.2 m·s-1，对应的系统效率变化范围为14.61%～15.24%.

4) 系统的运行需结合气象参数进行合理的调控，选择最优工况下的运行参数，以期获得最优的运行效果.