基于消费效用函数论等额本金法和等额本息法的差异

陈冠州，王禾

（1.五邑大学 经济管理学院，广东 江门 529020；2.广东南方职业学院 财经学院，广东 江门 529000）

按揭贷款是购房时常见的融资方法，而还款方法有等额本息还款、等额本金还款、等额递增还款、等额递减还款、按期付息还款和到期还本还款等. 其中，等额本息还款和等额本金还款是最主要的两种还款方法. 围绕等额本息还款与等额本金还款的优劣，不少学者与实务人士都进行过有意义的分析. 文献[1]通过定量分析明确地指出在多种常见情形下，借款人向银行已支付的总利息始终有等额本息方式下的支付额大于等额本金方式下的支付额，如果借款人对两种还贷方式的承受能力无差别，等额本金还款方式总优于等额本息还款方式. 文献[2]则运用文献资料法、案例分析法阐述了同样的结论. 运用类似手法进行研究并得到相同结论的还有文献[3-6]. 此外，有不少学者对等额本息还款与等额本金还款的现金流进行了公式化的分析[7-8].

围绕这两种还款方法进行研究的文献，大部分都着眼于进一步简化每期还款额度或还款总额的计算方式. 然而，现实中的贷款者在考虑选择哪一种还款方式时，其自身的因素，如贷款者的收入、对还款期限的选择、对现金流波动的厌恶程度和耐性等都会影响其决策，因此，在既往研究的基础上有必要进一步建立一个综合考虑以上因素的定量分析模型. 本文仍以按揭贷款购房为例，简要回顾基于还款总额的传统比较分析中的逻辑与结论，再从现值法角度对两种方法进行比较分析，最后通过引入经济学与金融学中常用的消费效用函数，对贷款者选择不同还款方法时所获得的效用进行建模和分析，进一步分析还款期数、购房者的收入、对延迟消费的耐性、风险厌恶程度等因素如何影响还款方式的选择.

1 模型回顾

等额本息还款是指借款人每期以相等的金额偿还贷款，按还款周期每期归还，在贷款截止日期前全部还清本息. 为了计算和说明的方便，我们把每期设想成每月，这也是最常见的还款周期. 一般而言，等额本息还款模型预设以下参数，月贷款利率R，总借款额B，月还款额P，还款期n. 根据月初贷款余额计算该月还款额中的各种现金流，包括所支付的利息以及偿还的本金，需注意，月还款总额固定，贷款利率在契约生成时固定. 设月初（即上月月末）贷款余额为L，月利息支付额为IP，月本金偿还额为BP，以上变量满足以下关系：

其中，t=1,… ,n；随着购房者如期缴纳最后一期欠款，贷款全部还清，即Ln=0. 通常情况下，贷款总额B与贷款利率R是已知的，而月还款额和还款期限由购房者与银行协商确定. 根据上述的变量关系我们不难发现月还款额与还款期限之间相互关联. 如果给定了还款期限，用数值计算能够方便地算出月还款额，实际上，我们利用每期还款额的现值之和等于总借款额这一关系可以轻易地推导出等额本息还款模型的月还款额的解析解：

另一种常见的还款方法是等额本金还款法，它指借款人每期须偿还等额本金，同时付清本期应付的贷款利息，而每期归还的本金等于贷款总额除以贷款期数. 实际每期还款总额为递减数列. 根据月初贷款余额计算该月还款额中的现金流，包括支付的利息和偿还的本金，月还本金一定，各变量须满足以下关系：

同样，t=1,…,n；随着购房者如期缴纳最后一期欠款，贷款全部还清.

2 比较分析

为了直观地比较两种还款方式的具体差异，我们采取数值分析方法. 设还款时间为10年，每月还款，则总期数为120；设贷款总额为50万元，年利率为5%，按银行常用折算方式得月利率为5%/12.按上一节的模型计算方法，可得模拟数据如表1，其中省略了11～114期数据.

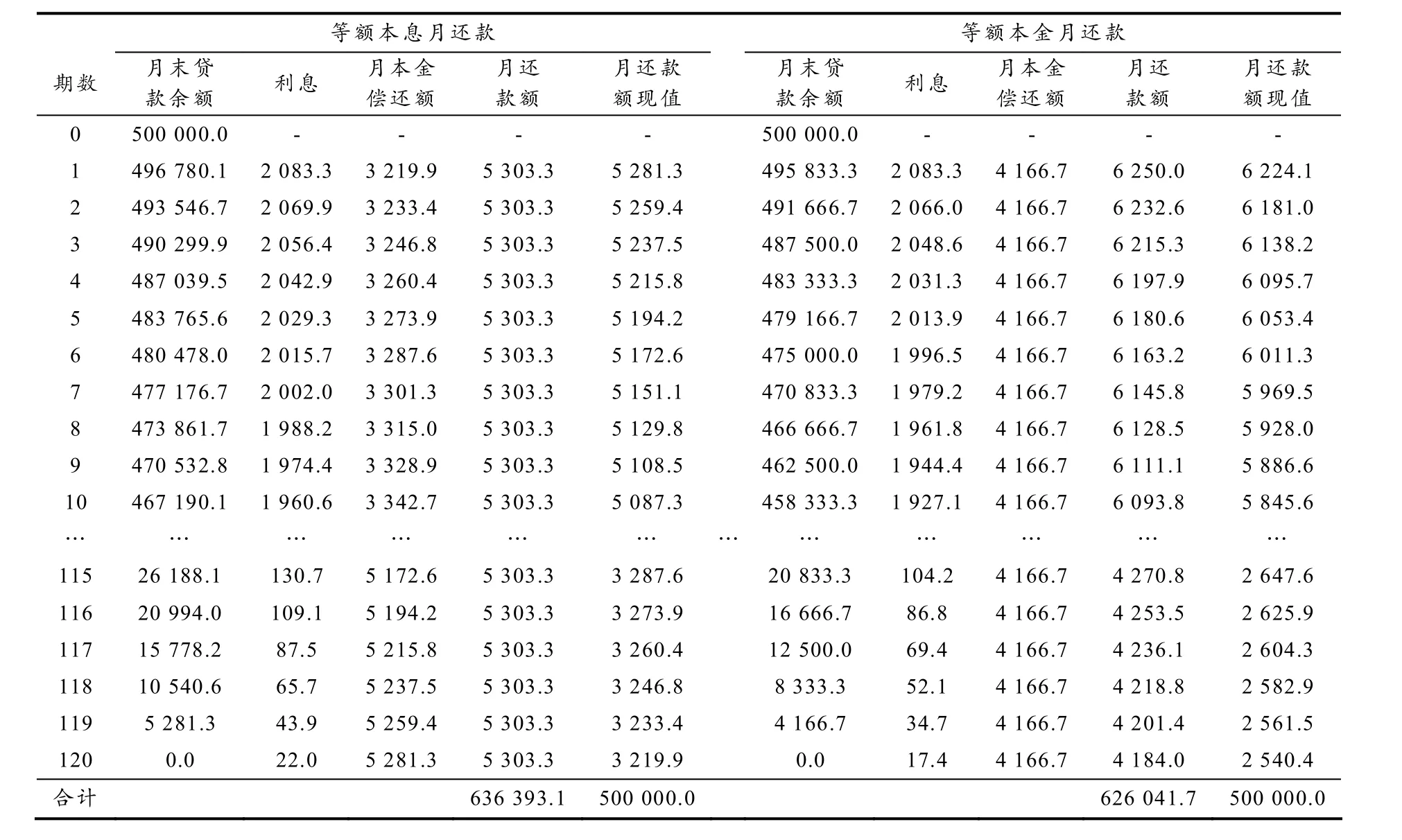
表1 模拟数据 元

2.1 还款总额分析

按表1数据绘制两种还款方式下每月还款额与累计还款额曲线，具体见图1.

图1-a能直观地看出：等额本息法每月还款额为5 303.3元，而等额本金法最初的还款额度最高，达到6 250元，但由于本金偿还的速度较快，随后月偿还额逐步递减，在60期之前已低至等额本息法的月还款额，到末期更低至4 184元. 因此，不少实务工作者会建议购房者在期初的时候艰苦一点偿还更多本金，随着时间的流逝，将来的房贷压力会越来越低. 当然，对等额本金法的推崇并不仅仅因为“先苦后甜”的理由，事实上，等额本金法的总还款金额要小于等额本息法的总还款金额，这一点我们能从表1的合计看出①有不少比较等额本金还款法与等额本息还款法的网站或广告宣称它们的还款总额是一样的，如何选取仅取决于购房者的资金计划，而通过精确计算我们能证明这种说法是误导..

图 1-b更方便读者观察整个还款期累计还款额的推移情况：还款期一开始并持续相当长的一段时间，等额本金法的累计还款额略高于等额本息法的累计还款额，这是因为前者对削减本金做出了更大的贡献，因此后期利息明显下降. 经过对比可知，在本文采用的比较符合现实的参数下，等额本息法还款总额会比等额本金法高出约1万元.

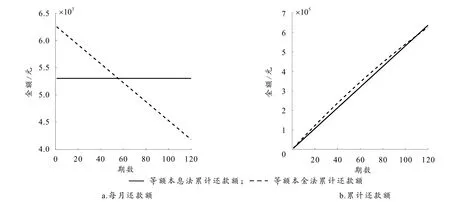
图1 两种还款方式每月还款额与累计还款额的比较

2.2 现值分析

尽管两种还款方式最终的偿还总额不同，但是从总现值的角度来看它们是相等的，均为借款总额50万元. 为了方便读者理解，我们用数学语言来表达，设偿还的现金流现值合计为B′，得

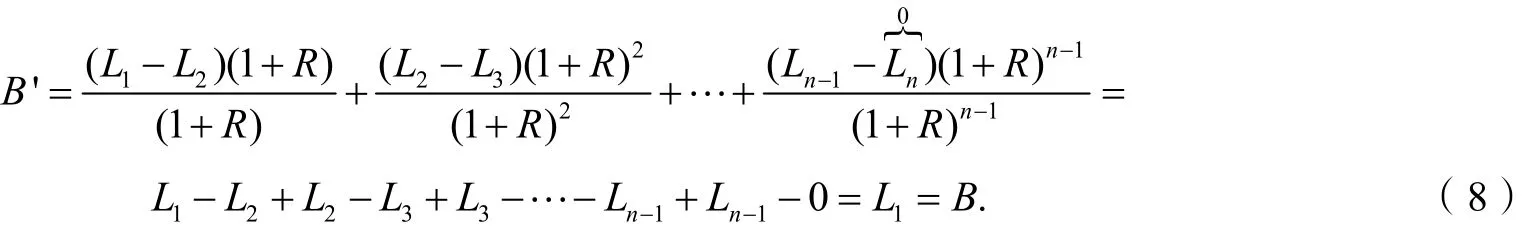
由式（8）可见，无论是等额本息还款法还是等额本金还款法，它们的现值之和都与借款总额相等. 那么，为什么在贷款买房的实际操作过程中，选择等额本息还款的人会多一些呢？有一个基于实务的有力解释是贷款审批资料里要求借款人提供近半年银行流水证明，且每月收入需要是月供的两倍，等额本金法比等额本息法初期月供要高，而且贷款年限越短，两者差距越大，所以等额本金法的贷款申请门槛相对更高，为了稳当地贷款买房，选择等额本息还款更容易一些，故选择等额本息还款的人会多一些. 那么除此以外是否还有别的原因？接下来我们从购房者的消费效用角度给出一个解释，证明即使没有上述实务操作中的限制，购房者也会主动选择等额本息还款法.

2.3 效用分析

不少研究按揭贷款方式的文献都着眼于现金流的变化、还款总额或还款期，但购房者决定按揭贷款的时候，必然会考虑到收入与消费的问题. 众所周知，消费给经济主体带来效用，在理性行为的角度看，一定期间内越稳定的消费越会给经济主体带来更高的总效用. 根据上述观点，我们引入购房者的月收入和效用函数对还款问题进行建模分析.

设效用函数u(C)，消费C=Y-P，其中Y为月收入. 为了更简单地理解本文主要结论，我们假设购房者月收入一定，每个月支付完按揭偿还额后的收入余额都用于消费，并给购房者带来效用. 因此在整个还款期间该购房者的总效用为

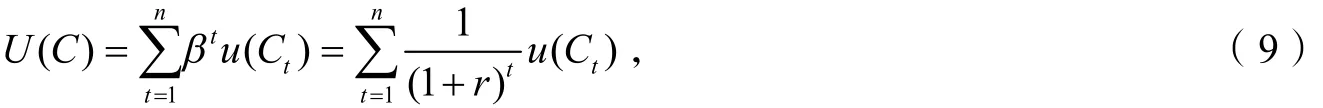
其中β为效用折现系数，r为所对应的效用折现率，

效用函数满足一阶导数为正、二阶导数为负，即满足“越多越好”和“风险厌恶”两个假设. 到此，只要设定效用函数的具体形式，即可检验各种变量对还款方式选择的影响. 效用函数具有多种经典的函数型，如线性效用函数、平方效用函数、幂指数效用函数、双曲线绝对风险厌恶效用函数等. 其中，幂指数效用函数具有常数相对风险厌恶系数的性质，在不产生重大影响下，更便于探讨模型性质，故下文将采用进行比较静态分析，读者可确认符合效用函数假设，且绝对风险厌恶系数相对风险厌恶系数为，为常数.

我们将采用比较静态分析法，即通过单独改变上述效用模型中特定的参数以观察购房者对还款方法的偏好会受到何种影响. 基本参数的默认值设定如下，月收入参照智联招聘公布的2018年底全国平均月薪值，约为Y=8 000；以不太介意净收入波动风险以及对延迟消费极具耐性的购房者作为参照标准[9-10]，即设相对风险厌恶系数γ=1.6，效用折现率r=0；还款期设为常见的10年，以月为单位得总期数n=120. 由MATLAB计算的数值比较静态分析结果如图2所示，纵轴代表购房者选择等额本息还款法时还款期间的总效用Uf与选择等额本金还款法时还款期间的总效用Uv之差，也可以理解纵轴代表的是购房者选择等额本息还款法是否会比选择等额本金还款法更加“幸福”. 此处需要注意，具有重要意义的是Uf-Uv的符号，而不是其数值大小，因为参数变化会对效用函数的基数产生明显影响，根据序数效用理论，两种还款方式所带来的效用不能简单加总求和，但能通过它们之间的大小关系表示出满足程度的高低与顺序.

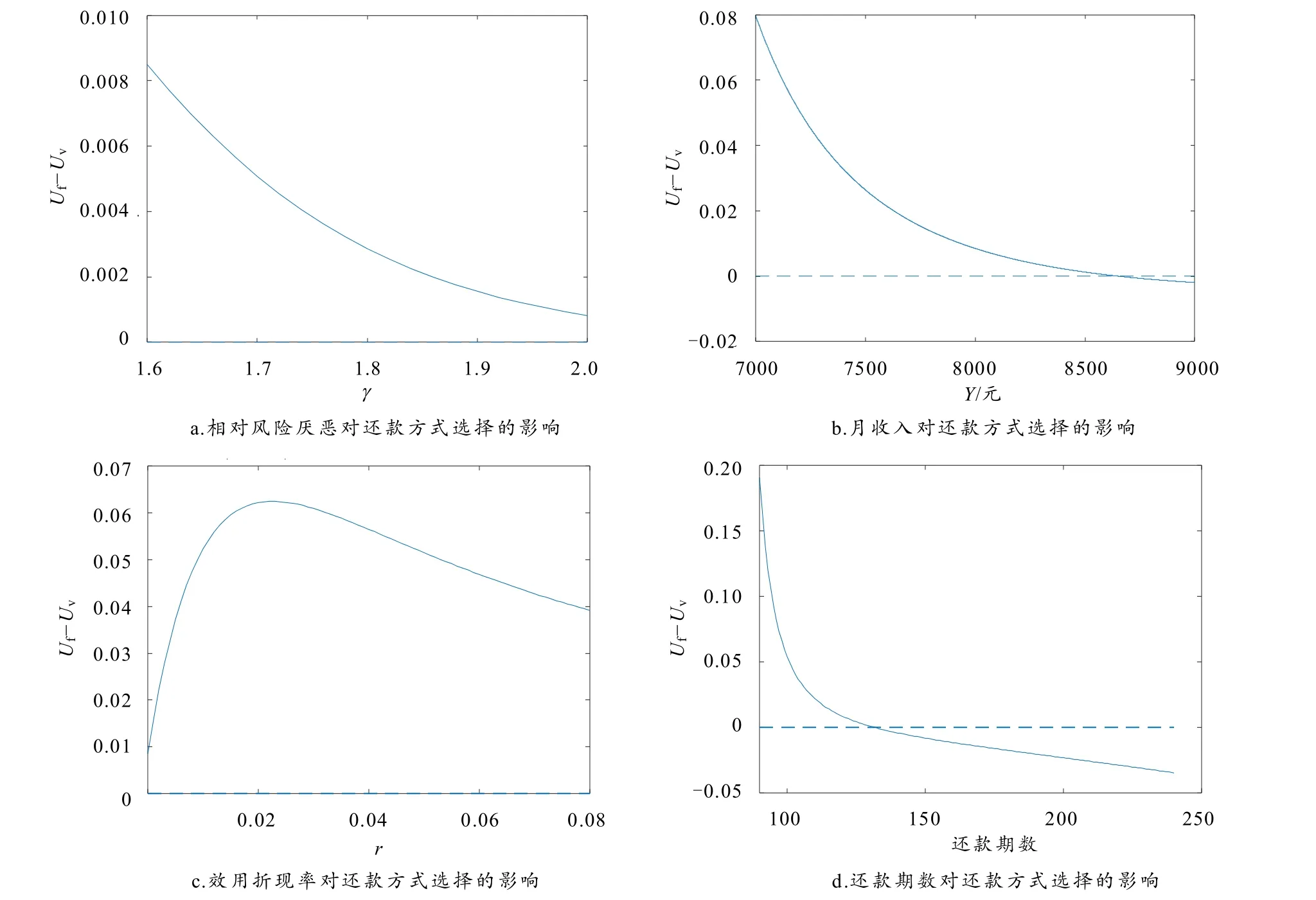
图2 比较静态分析

图2-a显示，在所选γ的变化范围内，Uf-Uv均大于0，也就是说，若购房者具有幂函数型消费效用函数，那么她将偏好于将来有稳定的现金流进行消费，故她应该选择等额本息还款法②可以确认，即使设定更大的γ，两还款方式的效用差fv U-U仍为正数但趋向于0，却不会为负..图2-b表明，在贷款总额、还款期等条件一定的情况下，若月收入较低，虽然选择等额本金还款法会让购房者在还款末期偿还较少的金额，但因前期还款压力过大，其总效用比等额本息还款法的总效用小，即Uf-Uv＞0；另一方面，如果购房者月收入较高（在此数值计算下，月收入大于约8 650元），购房者有相对充裕的收入来承受前期还款的压力，她可能偏向于选择等额本金还款法. 图 2-c显示，在其他参数不变的情况下，效用折现率在各种大于0的取值下，更安稳的还款方式会给购房者带来更高的“幸福感”；即使折现率等于 0，即购房者非常有“耐性”，她对现在的消费和将来的消费感觉完全一样，但在此参数条件下，她依然会偏向于选择等额本息还款法. 图 2-d显示，还款方式的选择会受到还款期的影响，尽管在本例中预设的10年还款期显示购房者会偏向于稳定的还款方式，但是若还款期变得更长，那么等额本金法的前期还款额也能变得更低，购房者生活能更加充裕，而后期更充裕的消费资金所带来的效用占据总效用的分量会更重，购房者更应考虑“先苦后甜”的效应而选择等额本金还款法.

3 结论

本文从还款总额、总现值和效用的角度对按揭贷款的两种常见方式，即等额本息法与等额本金法进行了比较分析. 分析结果一方面再次确认了在其他条件相同的情况下，尽管两种还款方法的现金流现值之和相等，但等额本息还款法所支付的总额大于等额本金法的总还款额；另一方面，分析指出，即使等额本息还款法的总还款额更高，但是购房者并不一定因此选择等额本金还款法. 如果购房者的收入较低，或还款期限不长，购房者将难以承受等额本金法所带来的前期还款压力，这种情况下“先苦后甜”的效应并不明显；购房者在做决策时会倾向于将来有稳定的消费现金流，反映了经典的凹性效用函数的性质. 通过建立效用模型，本研究把购房者的偿债能力更准确地量化，能为贷款购房人群提供有价值的理论指导.