基于Z-number Clouds距离的多属性决策模型及其应用

王翠翠

(安徽三联学院 基础部，合肥 230601)

一、引言

现实世界充满诸多不确定性，其中随机性和模糊性是不确定性最基本的表现形式。概率论和模糊数学是研究不确定性问题中的随机性和模糊性的主要工具。然而，概率论和模糊数学在刻画不确定性方面仍然存在诸多不足，1995年李德毅院士在概率论和模糊数学的基础上提出了云的概念，并研究了模糊性和随机性及其关联性。自云模型提出以来，云模型已被广泛应用于数据挖掘、自然语言处理、决策分析、智能控制、图像处理等领域[1]。一般来说，云模型的数字特征主要包括期望，熵和超熵[2]，其中期望表示云滴在论域空间分布的期望，代表定性概念的点。熵是用以度量信息不确定性程度，代表定性概念的可度量粒度，体现了云滴的离散程度以及云滴的取值范围。超熵则是熵的不确定性度量，反映了每个数值隶属这个语言值程度的凝聚性，也就是云滴的凝聚程度。所以，超熵越大，云的离散程度越高，隶属度的随机性也随之增强，云的厚度也就越大。

为了更好地描述决策问题中的模糊性问题，Zadeh于1965年提出模糊集(Fuzzy sets)理论[3]，现在已经被认为是处理决策问题中不确定性信息的有力工具[4-5]。2011年Zadeh提出了Z-number的概念，指出Z-number由A和B两个元素组成，它的构造把自然语言显示的客观信息和人为主观理解的成分并列表达，增强了人类对自然语言的理解[6]。自Zadeh提出Z-number的概念后，国内外学者主要从三个方面对Z-number进行了相关研究，第一个是Z-number的理论研究，与Z-number密切相关的概念，如Z-valuations[7]、Z-information[8]等；第二个是Z-number的相关计算，如Alive等人提出了离散Z-number[9]和连续Z-number[10]的相关计算，Qing等人对离散型Z-number提出了否定的看法[11]；第三个是基于Z-number的决策方法，如Kang等提出了基于Z-number的效用函数的决策方法[12]，Yao等提出了基于Z-number优势度的多属性决策方法[13]，Peng 和Wang研究了基于犹豫不确定语言型Z-muber的多准则群决策问题[14]，姚爱婷等人利用Z-number谱构建多属性决策模型[15]，邹斌构建新型Z-number熵并提出一种多准则群决策方法[16]。

鉴于云模型自身的数字特征可以较好地表达不确定环境中的随机性和模糊性，本文主要结合云模型和Z-number理论提出一种新型转换方法，由语言型Z-number表达的不确定性问题转换为ZCs问题，进而度量其不确定性。因此，本文在介绍语言型Z-number[14]和云模型[2]的概念基础上，结合两类语言尺度函数提出一种将Z-number转化为ZCs的新方法，通过定义两个ZCs的距离来度量ZCs的不确定性，进而基于ZCs的距离建立了一个新的多属性决策模型，并应用于新能源汽车性能评估问题中。

二、基础知识

定义1[6]假设si∈S是一个语言型语集，即S={si|i=0,1,2,…,2t}。假设现有一个数值变量θi∈[0,1]，设H是语言型语集si到θi的一个映射，即

H:si→θi(i=0,1,2,…,2t)

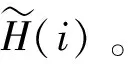
下面有两类语言尺度函数(LSF)[14]：

第Ⅰ类：

(1)

(2)

(3)

其中i=0,1,2,…,2t。

第Ⅱ类：

(4)

(5)

(6)

其中i=0,1,2,…,2t。

定义2[2]设U是一个论域，T为U中的定性概念，若一个随机变量x∈U，满足x～N(Ex,En′2)和En′～N(En,He2)，则x∈T的确定度y定义如下：

(7)

则称x的分布是一个标准云，记为C=(Ex,En,He)，称(x,y)为云滴，利用期望Ex，熵En和超熵He有效地刻画T在U中的特征。

定义3[6]Z-number是有序的一对模糊数，记为Z=(A,B)，第一个元素A是不确定变量X的实值函数，是对X在值上的约束；第二个元素B是对第一个元素A的可靠性的度量。当A,B都是语言型术语时，Z=(A,B)便是一个语言型Z-number。

三、语言型Z- number到云模型的转换方法和ZCs的距离公式

(一)语言型Z-number到云模型的转换方法

下面基于几类语言尺度函数，结合云模型的特征和分布提出一种新的转换方法。

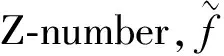
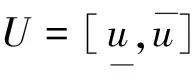
(8)

(3)计算熵值En，由标准云的特征x～N(Ex,En′2)正态分布的“3σ原则”可得到

(9)

(4)计算超熵值Hei，由标准云的特征En′～N(En,He2)可得到

(10)

当t=4时，即语言型术语集为S={s0,s1,…,s8}，选择语言尺度函数LSF1公式(1)和LSF5公式(5)，这里U=[0,10]，利用公式(8)(9)(10)计算ZCs的期望，熵和超熵对Z=(s4,s′3)进行转换得到Z-number云表示为ZC=((0.5,0.4196),(10,3.333,0.333))。

(二)ZCs的距离公式

下面将在上述转换方法的基础上定义了一个新的ZCs距离公式，用来度量两个ZCs之间的不确定性程度，距离越大即两个ZCs之间“相距”越远，其不确定性程度越大，反之不确定性程度越小。

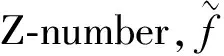
d(ZC1,ZC2)=

(11)

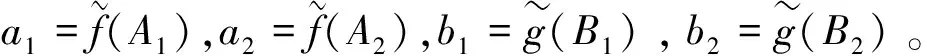
该距离公式充分考虑了两个语言型Z-number的不确定性，分别取两个语言尺度函数对语言型Z-number进行转换得到ZC，并对两ZC的数字特征运算进行λ次方并开方，从而有效地缩小了语言型Z-number在反应数据信息过程中表达的不确定性。

性质1假设ZC1,ZC2,ZC3是三个任意的Z-number，ZC的距离公式满足如下性质：

(1)d(ZC1,ZC2)≥0

(2)d(ZC1,ZC2)=d(ZC2,ZC1)

(3)d(ZC1,ZC2)=0,当且仅当ZC1=ZC2

(4)d(ZC1,ZC2)≤d(ZC1,ZC3)+d(ZC3,ZC2)。

四、基于ZCs距离公式的多属性决策方法

第一步：设A={a1,a2,…,an}为方案集合，C={c1,c2,…,cm}为属性集合，W={w1,w2,…,wm}为属性权重集合。

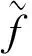
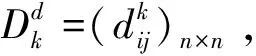
第四步：计算属性权重，即求解m个属性的权重向量W={w1,w2,…,wm}，基于概率法可定义属性权重为：

(12)

(13)

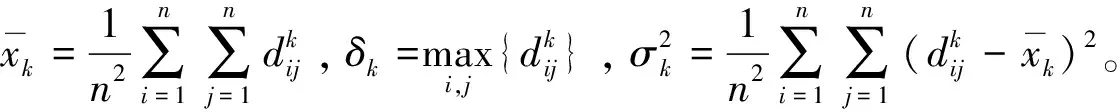
(14)

五、实例分析

随着我国对环境保护、技术进步和能源安全的重视程度不断加深，新能源汽车因其动力、价格、环保等优势逐渐成为汽车行业的重要品类，而其性能评估对于新能源汽车的发展至关重要。现在假设市场上有四种备选新能源汽车型号(方案)ai(i=1,2,3,4)需要评估，决策者利用语言评估标度S={s0,s1,s2,…,s8}={很差，差，较差，稍差，一般，稍好，较好，好，很好}和S′={s′0,s′1,s′2,…,s′8}={很不确定，不确定，较不确定，稍不确定，中立，稍确定，较确定，确定，很确定}对备选汽车型号的四个关键属性(汽车单次行驶里程、质量与技术水平、价格与成本、驾驶舒适水平)cj(j=1,2,3,4)进行决策。

第一步：四种不同型号的新能源汽车组成了方案集合A={a1,a2,a3,a4}，C={c1,c2,c3,c4}为属性集合，W={w1,w2,w3,w4}未知属性权重集合。表1为专家的决策矩阵。

表1 专家的语言型决策矩阵

第二步：将表1决策矩阵用公式(2)和(4)两个不同的语言尺度函数和新型转换方法将语言型Z-number转换为Z-number云矩阵DZC=(ZCij)n×m，其中令U=[0,10]。下面以属性c1为例展示决策矩阵由语言型Z-number转换为ZC：

ZC11=((0.5,0.580),(10,3.333,1.111))

ZC21=((0.309,0.667),(16.199,5.40,1.80))

ZC31=((0.691,0.5),(7.232,2.411,0.804))

ZC41=((0.146,0.77),(34.142,11.381, 3.794))

第三步：计算同一属性下任意两类汽车型号的ZC距离，可得到如下距离矩阵

第四步：由公式(12)和(13)可计算属性权重向量为

w′=[9.7726,9.7337,13.9976,10.9736],

w=[0.2197,0.2188,0.3147,0.2467]。

第五步：计算综合矩阵

第六步：计算有向距离矩阵

第七步：计算排序向量v=[8.5858,-0.7267,16.0153,-23.8744]，所以这四个方案的排序为a3≻a1≻a2≻a4，即综合四个属性因素可知第三种型号的新能源汽车为最优。

六、结语

本文结合语言型Z-number和标准云定义使用两类语言尺度函数提出了一种新的将Z-number转换为Z-number云(ZC)的方法，并定义了两个不同ZC的距离。利用新的转换方法和距离公式建立了未知属性权重的多属性决策方法，从理论方面计算出了合理的属性权重从而进行决策排序得到最优方案。利用云模型的处理定性概念与定量描述的不确定转换来确定自然语言型Z-number在多属性决策中表达的不确定信息，从而全面、直观地表达不确定性环境中的不确定信息。最后以一个新能源汽车性能评估为例验证了本文所提出决策方法的有效性和可行性。