(1+1)维水波方程的孤波结构

徐昌智 王红专

(金华教育学院，浙江 金华 321000)

孤立波是英国科学家罗素发现的。1871年，布森内斯克(Boussinesq)、1876年瑞利(Lord Rayleihg)分别从理想流体的运动方程导出孤波波形关系。1895年，德弗里斯(de Vries)和科特韦格(Korteweg)利用浅水中小振幅和长波运动的实验，建立了非线性浅水波方程，此方程后来演化为著名的非线性Korteweg-de Vries方程。关于非线性水波方程有许多类型，如(1+1)维浅水波方程、高阶浅水波方程、非线性Green-Naghdi水波方程等[1]。本文研究如下的(1+1)维水波方程[2]：

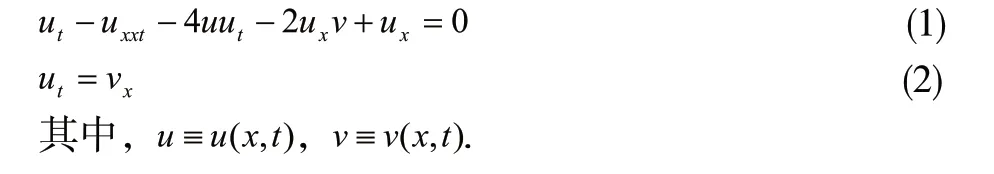
1 (1+1)维水波方程的试探解

非线性方程的求解方法，比较典型有对称约化方法、傅里叶级数展开方法、多线性变量分离方法、形变映射方法等[3]，本文采用齐次平衡方法，经研究分析可设方程(1)(2)有如下的解形式：

2 (1+1)维水波方程的孤波结构

则得到(1+1)维水波方程的物理场量 的稳定型双孤波结构，图1至图7分别是t=-7，t=-4，t=-1，t=1，t=5，t=7，t=9的波形图，图8是随时间变化的演化图形，从中可见2孤子稳定传播，并有一次相互作用，瞬时合为单孤波结构。

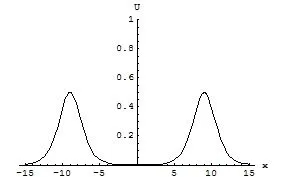
图1

图2

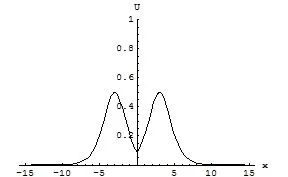
图3

图4

图5

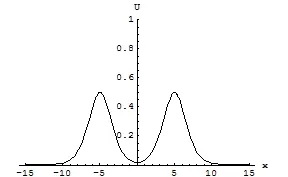
图6

图7

图8

如果任意函数 选取：

则得到(1+1)维水波方程的物理场量的非稳定型孤波结构，图9至图18分别是t=-4.5，t=-4，t=-3，t=-2，t=-1，t=0，t=1，t=2，t=3，t=4.5的波形图，图19是随时间变化的演化图形，从中可见该孤波只有在一定时间内出现，在时孤波消失。

图9

图10

图11

图1

图13

图14

图15

图16

图17

图18

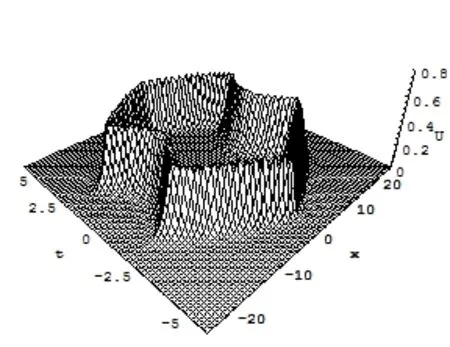
图1

如果任意函数 选取:

则得到(1+1)维水波方程的物理场量 的周期性孤波结构，图20至图26是在一个周期内，时间分别取t=0.01，t=0.1，t=0.3，t=0.5，t=0.7，t=0.9，t=0.99的波形图，图27是随时间变化的演化图形，从中可见该孤波的幅度在随时间变化，同时，发现有时出现双孤波结构，有时出现单孤波结构，但可以持续稳定波动。

图20

图21

图22

图2

图24

图25

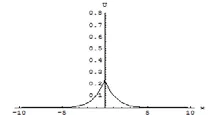
图26

图27

3 结语

通过齐次平衡方法研究(1+1)维水波方程(1)(2),获得了方程(1)(2)的二组新试探解，分析其物理场量 的解结构，找到了三种新类型的孤波结构，分别是稳定型双孤波结构、非稳定型孤波结构、周期性孤波结构，这不仅对(1+1)维非线性方程的孤波研究，特别是非稳定型孤波结构，以及(2+1)维非线性方程的孤波研究也有一定启示。