考虑跨线列车的高速铁路能力最大化合理利用研究
王宇强,魏玉光,商 攀,张进川
(北京交通大学 交通运输学院,北京 100044)
在高速铁路(以下简称高铁)运营管理过程中,列车停站方案、列车种类、开行区段及开行频率是在列车开行方案编制阶段基于客流需求优化得到的。近年来客流需求不断增长,所需开行列车数量增加,从而导致在铺画运行图时考虑到列车冲突问题可能无法得到一个包含所有列车的铺画方案。因此,如何优化利用高速铁路线路通过能力,以实现尽可能地开行更多列车,成为亟需解决的问题。影响高铁能力利用的因素众多,本文以列车停站方案和列车时刻表为对象展开研究。
目前,关于列车停站方案和时刻表的研究众多,但由于问题的复杂性,大部分学者将二者分开研究。在优化停站方案方面,文献[1]提出了一种0-1双层规划模型来解决列车的停站方案和旅客换乘选择问题,上层模型通过调整列车停站方案来最大化运营效益,下层模型目标为最小化乘客换乘时间。文献[2]通过在高峰时间段采用区域停站策略来最小化乘客出行时间和地铁运营成本。文献[3]建立了基于乘客总体出行时间最小的轨道交通列车跨站停车0-1整数规划模型,并利用禁忌搜索算法求解,最终通过算例验证了方法的可行性。文献[4]构建了旅客列车服务优化配置多目标规划模型,该模型通过协调列车停站方案和开行频率使运营总费用和乘客出行总时间最小。文献[5]基于多商品流问题构建了时间-空间-状态网,提出了以公平为导向的隔站停车策略,建立了线性优化模型,并采用拉格朗日松弛法算法求解。在优化列车时刻表时,文献[6]构建了累计流变量模型对高铁运行图进行优化,并设计了拉格朗日松弛算法求解,将复杂的列车组合优化问题转化为单列车的最短路径问题集合,从而降低求解难度。文献[7-8]建立了列车时刻表多目标优化模型来降低列车的能源消耗以及乘客的出行总时间。文献[9]构建了高铁通过能力最大条件下的运行图优化模型,根据列车运行过程中不得有冲突的特点将该问题抽象为时空网络中带约束的最大独立集问题。通过D-W分解将模型进行转化及线性松弛,最后采用列生成算法及分支定界算法求解。
但由于列车停站方案和时刻表的制定相互关联,越来越多的学者将两者同时优化生成。文献[10]提出一种新的多目标混合整数规划模型来同时优化列车停站方案和时刻表,目标函数为最小化列车的总停站时间和期望到达时刻与实际到达时刻之间的差值,最后使用Cplex求解。文献[11]构建了高铁时空网络,建立了使列车总收益最大的整数线性规划模型,然后使用基于列生成的启发式算法求解,最后在京沪高铁上验证了模型和算法的可行性。文献[12]构建的模型考虑了动态客流和线路设备能力,为每列车选择停站方案且优化时刻表,研究了动态客流的变化对列车时刻表及列车服务模式的影响。文献[13]分别以乘客时空可达性和列车运行可靠度为侧重点对高铁能力进行建模和求解,最后使用多智体仿真软件NetLogo,基于京沪高铁算例多模型进行了仿真实验。
既有文献大多以最小化列车总运行时间和最小化优化后时刻表与现有时刻表的差异为目标,较为缺乏以高铁能力利用为导向的研究。因此,本文研究以提高高铁能力利用为目标的列车停站方案和列车时刻表优化问题,其中高铁能力指在研究时间段内,高铁线路在一定的机车车辆类型,信号设备和行车组织方法条件下所能开行的最大列车数量。研究的主要内容为:
(1)将开行方案生成的需求列车集合分为高等级列车集合(停站次数较少但多为大站停车)与低等级列车集合(停站次数较多),保留高等级列车的停站方案,删除低等级列车的停站方案,通过优化生成所有需求列车的时刻表与低等级列车停站方案,将开行方案中确定的列车尽可能多地铺画到运行图中,从而优化高铁通过能力。两个列车集合中的列车通过运营商的决策确定,当运营商希望尽量满足乘客OD的直达性,提高高铁服务质量时,高等级列车数量大于低等级列车数量,当运营商希望在一定时间内开行更多列车时,低等级列车数量大于高等级列车数量。
(2)将跨线列车列入优化对象,进行本线列车和跨线列车的协同优化,定义从本线到其它线的跨线列车为本线下线跨线列车,从其他线到本线的跨线列车为本线上线跨线列车。
(3)构建基于高铁物理网的高铁时空络。基于高铁时空网络建立整数规划模型,目标函数为最大化高铁开行列车数和最小化列车总运行时间。为大规模案例设计了基于交替方向乘子法(ADMM)分解的算法,将原始问题中的困难约束作为惩罚项松弛到原目标函数中,提高了求解效率。
1 高铁时空网络的构建
高铁能力利用优化问题的本质为将有限的时空资源合理分配给各个列车的组合优化问题。因此可以通过构建时空网来描述高铁列车的运行过程。
图1为高铁物理网络,包括5个车站以及4个运行区段,其中车站3为跨线站。为构建高铁时空网,将车站分解为列车进站点和出站点,两点之间的连线表示列车的停站或跨线过程。同时,为在时空网络中完整地描述列车运行路径,新建表示列车在时空网中生成的列车生成点和列车在时空网中消失的虚拟到达点,见图2。

图1 高铁物理网

图2 改进后的高铁物理网
在高铁物理网的基础上引入时间维度且将时间离散为较小的单元(如1 min),构建时空网络(V,A),其中V为时空网中的顶点集合,A为时空网中的弧集合。V包括列车生成点、列车进站点、列车出站点和虚拟到达点。顶点(i,t)为在i点的t时刻;(i,j,t,s)为从(i,t)到(j,s)的一条有向弧。为了更好地描述高铁运行过程,设立7种类型的弧:
(1)区间运行弧(i,j,t,s)表示列车从k站列车出站点i的t时刻运行到k+1站列车进站点j的s时刻,见图3(a)。本文设立两种类型的运行弧,分别为高速列车运行弧集合Ag和中速列车运行弧集合Ad,(i,j,t,s)∈Ar,Ar=Ad+Ag,Ar为列车运行弧集合。
(2)始发列车进站弧(i,i′,t,s)表示始发列车进入k站到发线的作业过程,而在k站的上线跨线列车可以视为在本线k站的始发列车,通过连接k站的列车生成点i与k站的列车进站点i′生成,见图3(b)中的第ⅰ类弧,(i,i′,t,s)∈As,As为始发列车进站弧集合。

图3 时空网中各类弧的构建
(3)终到列车出站弧(i,i′,t,T)表示终到列车离开k站到发线的作业过程,在k站的下线跨线列车可以视为在本线k站的终到列车,通过连接k站的列车出站点i与k站的列车虚拟到达点i′生成,如图3(b)中的第ⅱ类弧。其中,T为时空网络的时间界限,(i,i′,t,T)∈Az,Az为终到列车出站弧集合。
(4)停站弧(i,i′,t,s)∈Aw与跨线弧(i,i′,t,s)∈Ac表示列车在k站的停站作业和跨线作业,Aw为停站弧集合,Ac为跨线弧集合。停站时间或跨线时间加起停附加时间为s-t。列车的最大、最小停站时间通过时空网中停站弧的时间权重来确定。两类弧通过连接k站的列车进站点i与k站的列车出站点i′而生成,如图3(b)中的第ⅲ类和第ⅳ类弧,其中3种不同时间权重的弧代表不同的停站时间,时间权重最大和最小的弧可以表示相应的列车最大、最小停站时间。
(5)通过弧(i,i′,t,t)表示不停站列车直接通过车站,为一条平行于纵轴的弧,该弧通过连接k站的列车进站点i与k站的列车出站点i′生成,见图3(b)中的第ⅴ类弧,(i,i′,t,t)∈At,At为通过弧集合。
(6)虚拟运行弧(i,j,t,T)表示有些需求列车在能力饱和情况下需要到达终点必须选择的弧,通过连接各列车始发站的列车生成点i与终到站的虚拟到达点j生成,(i,j,t,T)∈Adummy,Adummy为虚拟运行弧集合。
在建立的时空网络中,运行弧,停站弧、跨线弧、始发列车进站弧和终到列车出站弧的费用为列车的实际作业时间,通过弧的费用为0,虚拟运行弧的费用为无限大,如9 999。
2 模型的构建
2.1 模型假设
在构建模型前,提出以下假设:
(1)只选择线路的一个方向(称为正向)进行研究,另一个方向(称为对向)可同样利用此方法优化。
(2)各列车在各区段内的运行时间固定且已知。
(3)列车的起停附加时间固定且已知。
(4)最小列车间隔时间固定且已知。
(5)不考虑车底的运用情况。
2.2 构建模型
本文提出的整数规划模型中,输入参数为:列车的开行方案,包括列车运行区段、列车种类、列车开行数量以及高等级列车的停站方案;列车的最小列车间隔时间;不同速度等级的列车在各区段的运行时间;不同停站弧和跨线弧的时间权重;各列车的最大最小出发时间。模型的输出结果为:列车时刻表以及低等级列车停站方案。
由于列车的停站、跨线、运行等作业都可用时空网中不同类型的时空弧表示,因此高铁运行时刻表与停站优化问题可以建模为具有边际条件约束的网络多商品流优化问题。模型目标函数为
(1)

式(1)表示最大化列车集合K(K=K高∪K低,K高、K低分别为高等级列车、低等级列车集合,集合K内列车根据现有开行方案确定)在研究时间段内选择运行弧的数量,即最大化列车开行数。
为了方便算法的求解,我们将其转换为
(2)
式中:ci,j,t,s为时空网中每条弧的费用。
转化目的为最小化列车在研究时间段内的总费用。由于虚拟运行弧的ci,j,t,s为一个特别大的值,所以通过阻止列车选择虚拟运行弧,也就是通过最小化整个研究时间段内的总费用来最大化列车开行数。
模型约束条件为:
(1)高铁始发列车、终到列车停站约束
(3)
(4)
为了尽可能的如实反映列车运行的全过程和跨线列车的跨线过程,引入高铁始发列车、终到列车停站约束,对于跨线列车而言,始发列车进站弧实际描述了跨线列车在本线生成的过程,终到列车出站弧实际描述了跨线列车从本线消失的过程。该约束表示始发列车以及本线上线列车必须在其始发站进行停站作业或跨线作业,而终到列车以及本线下线列车必须在其终到站进行停站作业或跨线作业。
(2)跨线列车跨线约束
(5)
式中:Kk为跨线列车集合。
由于跨线列车a∈Kk在进行跨线作业时会切割车站咽喉,造成更多的等待时间,在时空网中则反映为跨线列车a∈Kk在跨线站必须选择跨线弧(i,j,t,s)∈Ac。
(3)高铁列车速度约束
(6)
本文设立了两种速度类型的高速铁路列车,分别为中速列车集合Kd,高速列车集合Kg,且设立了两种类型的列车运行弧,分别为中速列车运行弧Ad,高速列车运行弧Ag,该约束规定了高速列车可以选择中速列车运行弧运行而中速列车禁止选择高速列车运行弧运行。
(4)流平衡约束

(7)
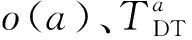
(5)列车停站次数约束
∀k∈Si,i′∈Vk
(8)
式中:vk为车站k为了满足乘客OD的可达性而需要的列车最小停站次数,vk的值通过现有的开行方案确定;S为高铁车站集合;Vk为高铁车站k的顶点集合。在高等级列车停站方案确定的基础上,该约束规定了各车站对于停站次数的需求。
(6)最小列车间隔时间约束
(9)
式中:φ(i,j,t,s)为列车冲突弧集,φ(i,j,t,s)∈Ar∪Az。
式(9)表示了列车在高速铁路运行中的安全因素,前车与后车的出发与到达时间间隔必须大于等于相应的最小列车间隔时间,即在(i,j)间,如果有一条运行弧或终到列车出站弧(i,j,t,s)被列车a选中,那么φ(i,j,t,s)∈Ar∪Az内的所有弧将禁止被选用。
(7)列车出发时间约束
(10)

该约束规定了列车a在其起始站的出发时刻不能早于最小出发时刻,也不能晚于最大出发时刻,运营商根据客流需求规定了某些或全部列车的出发时间段,对于大规模网络问题,该参数可参照以往时刻表来确定。

3 基于ADMM分解的算法求解
本文提出的整数规划模型在处理小规模案例时可以直接用Cplex求解,当计算大规模案例时,模型中的困难约束(如式(8)、式(9))会引发大规模列车组合,Cplex无法在短时间内求得最优解。所以提出基于ADMM分解的算法对大规模案例进行求解,ADMM分解算法为增广拉格朗日松弛与块坐标下降法的结合。
拉格朗日松弛是将原模型中的困难约束松弛,并引入拉格朗日乘子,将其乘积作为惩罚项带入原目标函数中,则原问题可分解为多个独立的子问题。增广拉格朗日松弛是在拉格朗日松弛的基础上,为提高解的质量,再为目标函数引入一个非线性的二次惩罚项。通过块坐标下降法将增广拉格朗日松弛问题线性化,按照顺序依次求解各子问题从而求得最终解。该方法可以解决拉格朗日松弛后带来的对称性问题,加快收敛速度提高算法效率[14]。
通过使用基于ADMM分解的算法,引入拉格朗日乘子λi,j,t,s和μi,j,t,s以及二次项惩罚乘子ρ和ρ′,将复杂约束式(8)、式(9)松弛且作为惩罚项添加到目标函数式(2)中,得到新的目标函数
约束条件为式(7)、式(10),则原问题变为基于时间的最短路径问题,各个列车的最短路径相互独立。
每列列车的最短路径目标函数为
(12)

通过公式推导得到
(13)
式中:
(14)
推导过程见文献[14]。基于ADMM分解的算法步骤为
Step1初始化迭代次数n=0,初始化拉格朗日乘子λi,j,t,s=0,μi,j,τ=0和二次项惩罚乘子ρ、ρ′,生成初始下界解{Xlower}和上界解{Xuper},设置最优下界LLB=-∞,LUB=+∞。


Step4更新拉格朗日乘子:
∀(i,j,t,s)∈Aw∪Ac
∀(i,j,t,s)∈Ar∪Az
Step5如果n等于预先设好的最大迭代次数,终止算法,否则,n=n+1转到Step2。
4 案例验证
以京沪高铁为例,通过优化生成所有列车的时刻表与低等级列车的停站方案,在考虑跨线列车的情况下优化其能力利用。提出的算法将在Python平台上实现,算法运行环境为一台内存16 GB,CPU:i7-770HQ 2.80 GHz的台式计算机。
京沪高铁共有23个站,各种类列车在各区段的纯运行时间见表1,本文规定最小列车间隔时间为4 min,起停附加时间为2 min,研究的时间总长度为10 h,时间离散化后的单位时间为1 min。京沪高铁为双线铁路,本文仅考虑北京南—上海虹桥方向的高铁列车。表2为各列车的运行区段和开行数,由现有开行方案确定,本文不研究列车开行方案的生成,所以需求数为假设但大于研究时间段内的理论通过能力,其中跨线列车包括7列正向跨线列车,高等级列车集合为北京—上海的高速列车以及北京—南京的高速列车,其余列车为低等级列车。由于篇幅有限,本文针对高等级列车集合与低等级列车集合的划分仅进行这一个实验,其他情况可按相同方法进行优化。由于京沪高铁跨线列车众多,本文只选取在徐州东站进行上线、下线的跨线列车为研究对象。
分别使用基于ADMM分解的算法和基于拉格朗日松弛的算法优化整个京沪高铁的能力利用,迭代次数200次,两种算法求解时间分别为22 126 s与20 194 s。运行图铺画结果见图4,目标函数值的上界,基于ADMM分解算法的下界和基于拉格朗日松弛算法的下界随迭代次数变化曲线见图5,其中上界与基于ADMM分解算法的下界间隔为1.56%,上界与基于拉格朗日松弛算法的下界间隔为6.83%,且基于ADMM分解算法的收敛速度明显优于基于拉格朗日松弛算法的收敛速度,基于ADMM分解算法第46次迭代时的目标函数值就达到了基于拉格朗日松弛算法的最优下界。
图4中北京南—上海虹桥方向的本线和跨线列车由于最小列车间隔时间约束,列车出发时间约束和列车停站次数约束的限制,影响了研究时间段内的最大通过能力,最大开行数为55列,运行线。为了更直观的体现跨线列车对本线列车能力的影响,进行的另一个实验将北京南—上海虹桥方向的跨线列车改为本线列车,实验结果为在相同研究时间段内可开行57列列车,比考虑跨线列车的情况多2列,证明跨线列车对本线列车的能力有很大的影响,在研究高速铁路能力优化时考虑跨线列车的影响更符合实际情况且非常必要。

表1 列车在各区段的运行时间 min

表2 列车OD及对应的列车数量
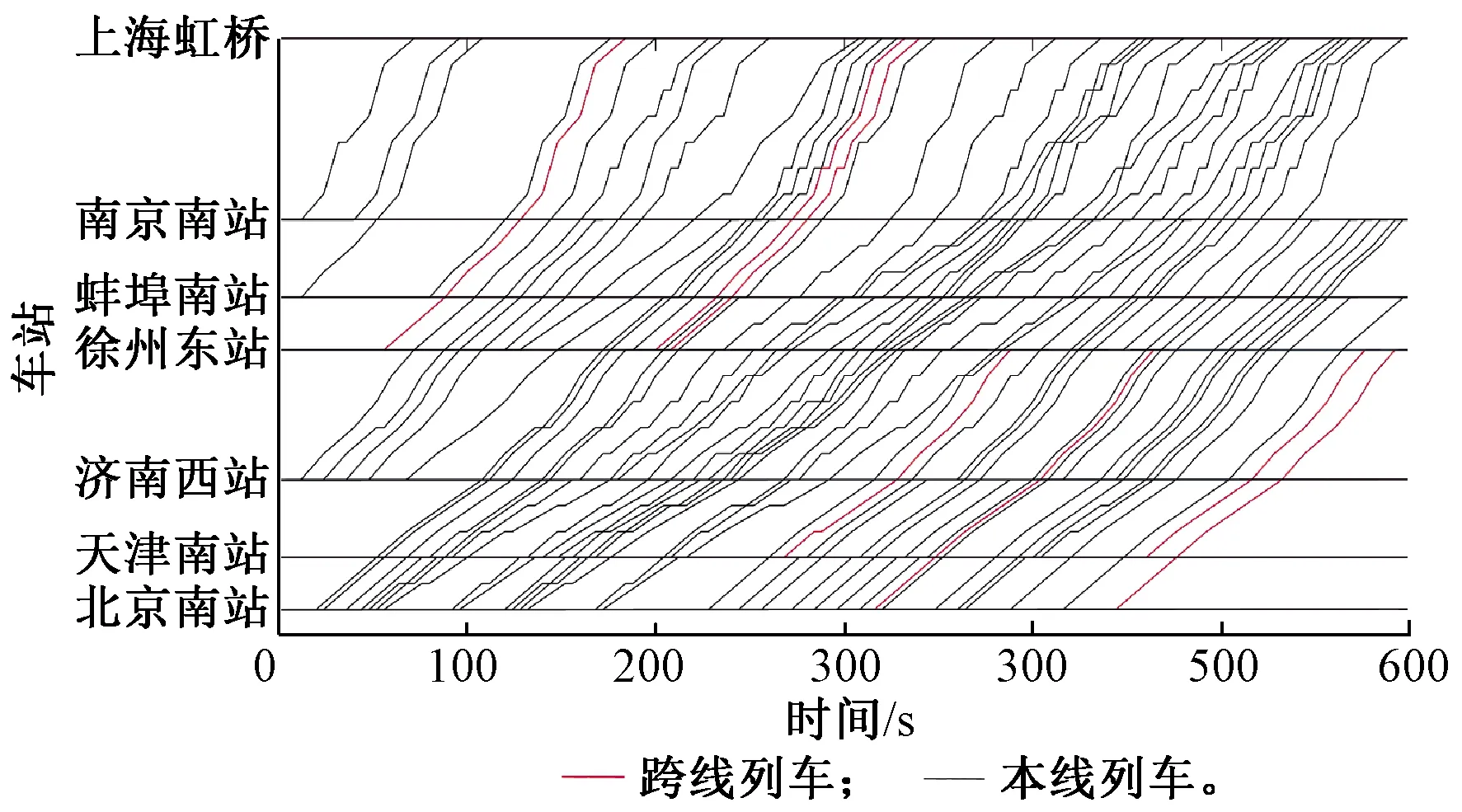
图4 北京南—上海虹桥方向列车运行图

图5 上下界随迭代次数变化曲线
5 结论
本文基于高铁物理网构建了高铁时空网,列车的停站作业和跨线作业可以直接使用停站弧和跨线弧来表示,而跨线列车的上线和下线作业分别可以看作是本线列车的始发和终到作业,基于此,将跨线列车纳入研究对象,提出了一种高铁最大通过能力下优化生成列车时刻表和停站方案的整数规划模型。
由于所研究的问题规模很大,设计了基于ADMM分解的算法对模型进行求解,结果表明本文提出的算法与基于拉格朗日松弛的算法相比,可以在较短时间内得到收敛且目标函数值上下界的差值更小。
本文对于列车的停站需求处理不够完善,没有充分考虑客流OD的直达性与时间分布差异性,在未来的研究中我们会将动态客流需求作为模型输入从而生成列车停站方案和时刻表以及进行客流分配,确保乘客OD的直达性以及考虑客流在时间分布上的差异性。且会提出更有效率的算法来扩大研究案例的规模,同时优化两条及两个方向的高铁线路通过能力。

