基于改进DE 的城轨列车节能速度曲线研究

聂莹莹，谢 刚，郭彦宏，董渠江

（1. 西南交通大学 信息科学与技术学院，成都 610031；2. 中铁二院工程集团有限责任公司 通信信号研究设计院，成都 610031）

城市轨道交通在为居民提供便捷乘车服务的同时也产生了巨大的能源消耗[1]。据统计，牵引能耗为列车运行的主要消耗[2]。荀径对列车节能操纵优化求解方法进行了综述[3]；许立、耿晨歌采用遗传算法对列车运行速度曲线生成进行研究，但评价模型过于苛刻[4-5]；丁圣采用非支配排序遗传算法研究列车多目标操纵优化，运算复杂度较高[6]；刘炜采用时间逼近搜索算法建立节能优化模型，但未考虑舒适度要求[7]。本文根据惰行控制理论[8]，建立分段渐进式的评价模型，并将舒适度要求纳入约束条件，采用改进的差分进化（DE，Differential Evolution）算法研究列车节能优化速度曲线的生成，以减少列车牵引能耗。

1 问题分析与模型构建

1.1 问题分析

城轨列车节能问题本质上是一个多目标优化问题，包含列车准时到达、定点停车和牵引能耗最小的目标。多目标问题求解可将多目标转化为单目标，或是直接采用多目标优化方法。采用Pareto 非支配排序方法可对多目标问题进行求解[9]，但实验研究表明，仅数代之后，种群中的个体都进化为Pareto 非支配个体，此时再将Pareto 非支配个体作为最优解的评价标准将失去意义[10]。因此本文采用建立各目标的评价模型，再通过权重分配合成单目标的方法。

1.2 力学模型与能耗计算

本文采用多质点列车模型，遵循如下假设条件：

（1）列车为质量分布均匀的刚体,是由足够多数量的质点组成的质点链；

（2）不考虑车钩间作用力对列车的影响；

（3）牵引和制动级位各5 级。

在列车运行过程中，作用在列车上的运行方向的力分为3 类：牵引力、运行阻力和制动力。

以列车沿斜坡向上运行为例，如图1 所示，其中F、B、W分别为列车受到的牵引力、制动力、阻力，F与运动方向一致，B、W 与运动方向相反；N 为支持力；G 为重力。则列车沿运动方向所受合力Fh为：

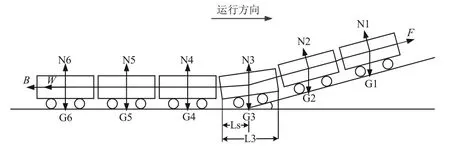
图1 列车受力分析

列车牵引力、制动力主要与列车型号、列车运行速度有关。当列车处于牵引状态时，B为0；处于惰行状态时，F和B均为0；处于制动状态时，F为0。

列车运行阻力一般由基本阻力和线路附加阻力组成。基本阻力公式如下：

其中，w0为单位基本阻力；a、b、c为经验常数，v为列车速度。

线路附加阻力主要包括坡道附加阻力和曲线附加阻力。当单列车厢处于不同的坡道上时，其坡道附加阻力ws为：

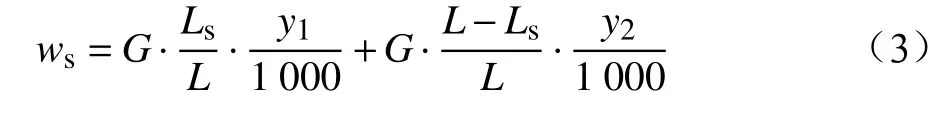
其中，车厢一长为Ls部分处在千分坡度数为y1的坡道上，车厢另一长为L-Ls部分处在千分坡度数为y2的坡道上；G为该车厢重量。如果单列车厢位于同一坡道，则只需计算该公式的前半部分即可。

同理，单列车厢位于不同的曲线半径，其曲线附加阻力wr为：

其中，车厢一长为Lr部分处在半径为R1的弯曲线路上，车厢另一长为L-Lr部分处在半径为R2的弯曲线路上。

将各个车厢所受阻力相加，即为列车受到的总阻力W。

其中，i为车厢号，i=1，···，n，n为车厢数；A为列车加速度；r为列车旋转质量系数，M为列车质量；以时间步长0.1 s，得到列车在各时间步长内的参数计算公式。f_force(v，ws)、f_brake(v，ws)分别为牵引力、制动力计算函数，与列车速度v和工况状态ws 有关。

牵引能耗是列车运行过程中牵引力做的功，计算公式如下：

其中，n为根据牵引力的改变而划分的区段数；Fi、ΔSi分别为第i段的牵引力和牵引力作用的距离；i=1，···，n；E为列车牵引力在站间所做的功，即牵引能耗。

1.3 列车运行工况转换原则

根据惰行控制方式，列车运行由牵引、惰行和制动3 种工况组成，工况转换需要满足转换规则才能进行，如表1 所示。

2 改进DE 算法

DE 算法是Rainer Storn 等人于1995 年提出的一种采用实数编码模拟生物进化的算法，具有高效的全局搜索效果和收敛性能[10]。但在求解多目标最优化问题时，有易过早收敛、陷入局部最优等问题。本文对现有的DE 算法进行改进，根据多目标优化的特点提出了新的交叉策略，提升基于DE 进化策略的收敛性能和全局搜索能力。

改进算法对种群进行约束条件下的初始化，经变异和改进的交叉策略，再通过评价模型得到个体适应值，选出高适应个体组成下一代种群，使种群进化反复循环，直到满足终止准则，则算法结束，如图2 所示。

表1 工况转换规则

图2 改进DE 算法流程

2.1 个体基因设计与初始化种群

本文采用位置与工况状态值组合的实数编码对个体基因进行设计，位置向量组和工况状态组均包含D 个点，起始点位置为0，工况状态为牵引工况，末点位置为目标停车点Se、工况状态为制动工况。种群的个体基因组合GE 为：

其中，gi表示第i个点的个体基因，i=1，···，D，由位置si和工况状态值wsi组合而成。

根据1.2 小节的假设条件，牵引和制动级位各5 级，如表2 所示。其中工况值1 ～ 5 分别代表制动输出19%、39%、59%、79%、99%，6 ～ 10 分别代表牵引输出19%、39%、59%、79%、99%。

表2 工况状态值

在种群初始化过程中，生成的个体需要约束，以筛选初始种群，其流程如图3 所示。

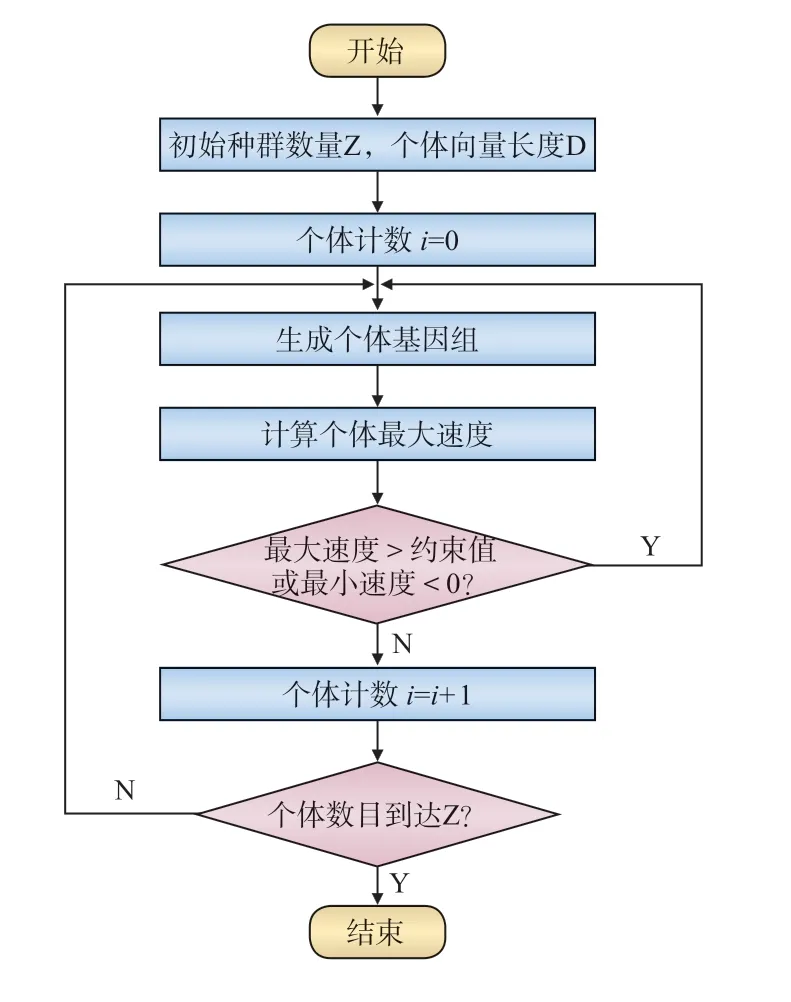
图3 种群初始化流程

2.2 约束条件分析

本文以区间限速、最大加速度、最大减速度、运行工况转换原则和牵引制动特性做为约束条件，将舒适度也纳入其中[11]，约束条件为：

其中，Jve、Jse、JE和Jte分别是末速度、末位置、牵引能耗和运行时间评价值；q、p、y分别是末速度、能耗和末位置评价值所占适应度函数的权重，1-q-p-y为运行时间评价值的权重，min 为所有个体中的最小值；wsRequire 为工况评价值，为true 表满足工况转换原则；workstate 为列车运行工况转换序列；workStatePrncp 是工况转换原则判断函数；Co为舒适度评价值，其值小于4 时，舒适度满足要求；vt、at、dt、Ft、Bt分别为t时刻列车运行速度、加速度、减速度及受到的牵引力、制动力；Ft,max、Bt,max为t时刻可输出的最大牵引力、最大制动力；Vt,max为线路在时刻t的最大允许速度；Amax、Dmax为最大允许加速度、最大允许减速度。

2.3 目标评价模型与终止准则

为了保证个体较好的适应性和全局收敛性，结合本文的节能优化模型，基于Matlab 进行实验仿真，建立了分段渐进式评价模型，如图4～图7 所示。评价模型在形式上保持一致，可有效抑制种群优化趋势向某个目标倾斜，保证种群优化的目标多样性。

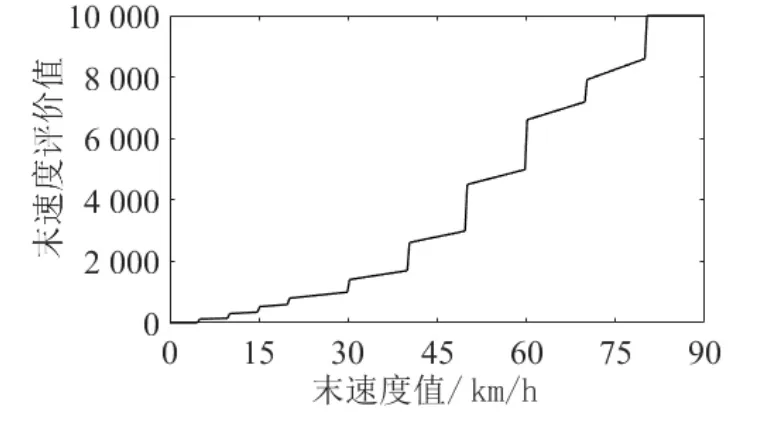
图4 末速度评价模型

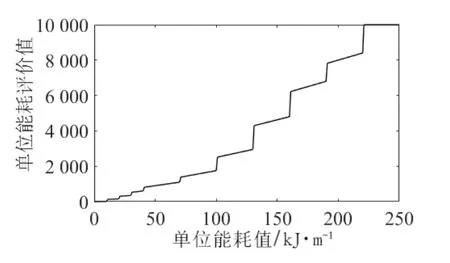
图5 牵引能耗评价模型

图6 停车位置误差评价模型

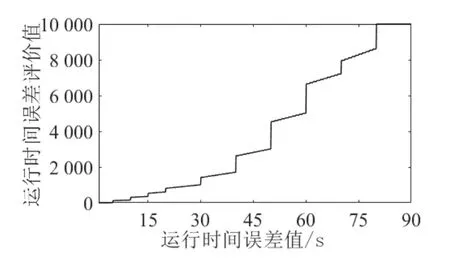
图7 运行时间误差评价模型

末速度评价模型对个体的末速度在0 ～ 80 km/h之间进行分段评价，其评价值范围为0 ～ 10 000，末速度超出80 km/h 按最高记。牵引能耗评价模型、停车位置误差和运行时间误差评价模型也类似。

种群终止准则是种群停止进化的一个标准。根据实测数据，如图8 所示，在60 代以内的收敛幅度较大，60 代以后，收敛幅度趋于平缓。故本文设置迭代次数为100，即可达到预期效果。

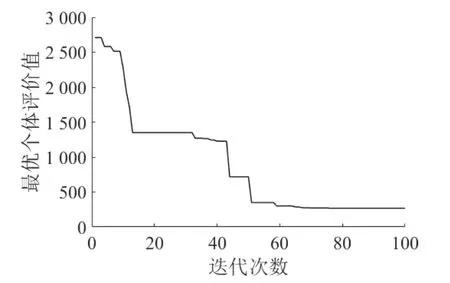
图8 迭代次数与评价值

3 算法参数设计与中间参数生成

改进DE 算法包含2 个重要参数：缩放因子和交叉概率。

3.1 缩放因子

缩放因子Fs是控制差分矢量对基向量影响大小的参数。本文对Fs的取值进行了测试，Fs为0.5 时，收敛效果好，如表3 所示。

表3 缩放因子对收敛的影响

3.2 交叉策略的改进

为进一步增强种群多样性，DE 算法交叉目标个体Xk(ts)与变异个体Vk(ts+1)，产生候选个体Uk(ts+1)，ts代表迭代的代数，k表示第k个个体。

采用DE 算法的交叉策略求解发现，下一代个体中变异个体较少，使算法的收敛效果较差。个体被淘汰的原因有：变异个体的基因值不符合个体基因向量组的要求，交叉概率使一部分个体淘汰。

为使变异个体有效，对变异策略进行如下改进：

（1）对变异的无效个体进行有效化处理。

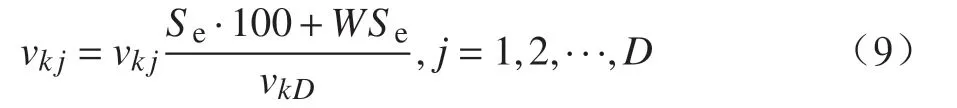
其中，vkj和vkD分别为变异个体Vk(ts+1)中的第j维分量和第D维分量，WSe为制动工况值。

（2）增大交叉概率为1，使收敛效果最好。

3.3 中间数据生成

图9 为个体末速度生成流程，其他数据生成也类似。

图9 个体末速度生成流程

4 算例分析

本文采用文献[7]中提供的上海地铁的线路数据，如表4～表6 所示；实现带线路区段限速的列车自动运行（ATO，Automatic Train Operation）曲线生成。列车型号为AC-03，车长144 m，AW2 质量327.6 T，牵引特性[8]如图10 所示。

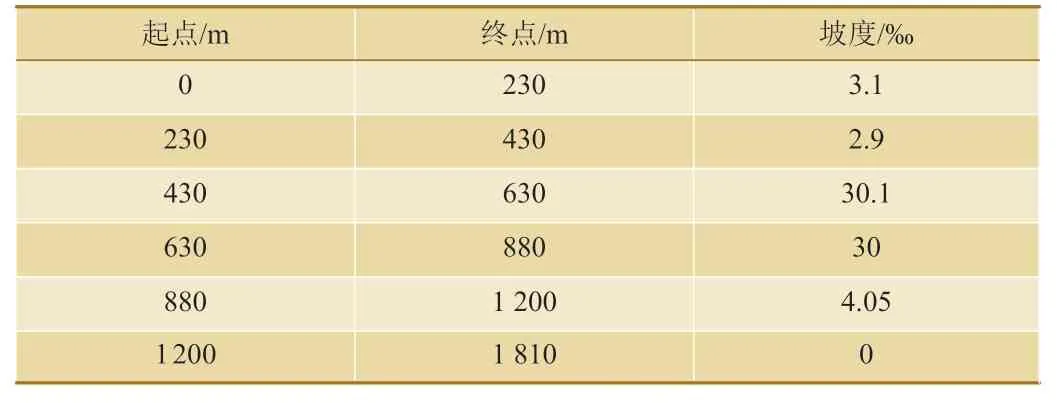
表4 线路坡度

表5 线路曲线

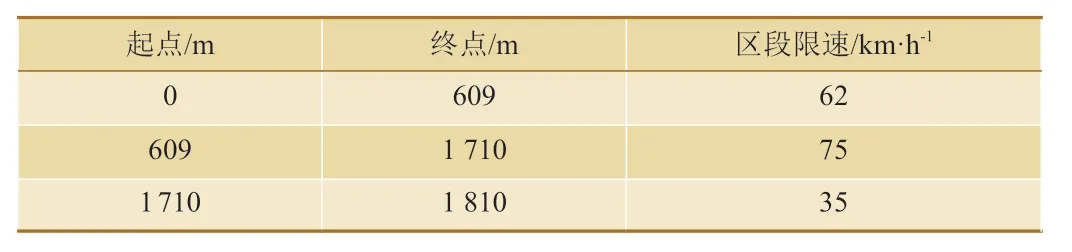
表6 线路限速

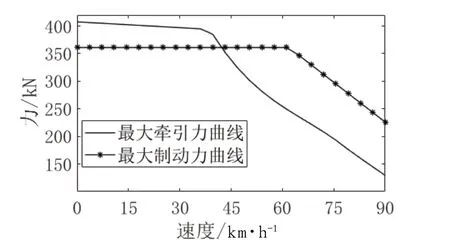
图10 AC03 牵引制动特性曲线

如图11 可知，随着迭代次数的增加，个体评价值不断减小，个体适应度不断提高，表明算法的收敛效果良好。

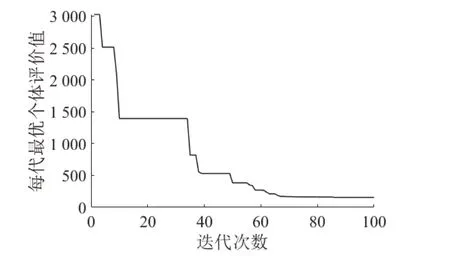
图11 100 代最优个体评价值

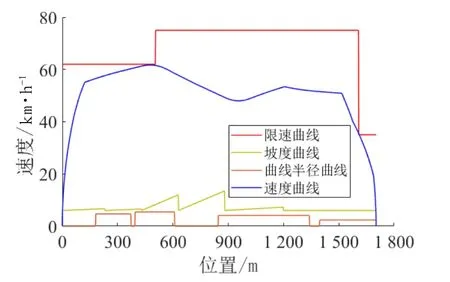
图12 最优ATO 速度曲线

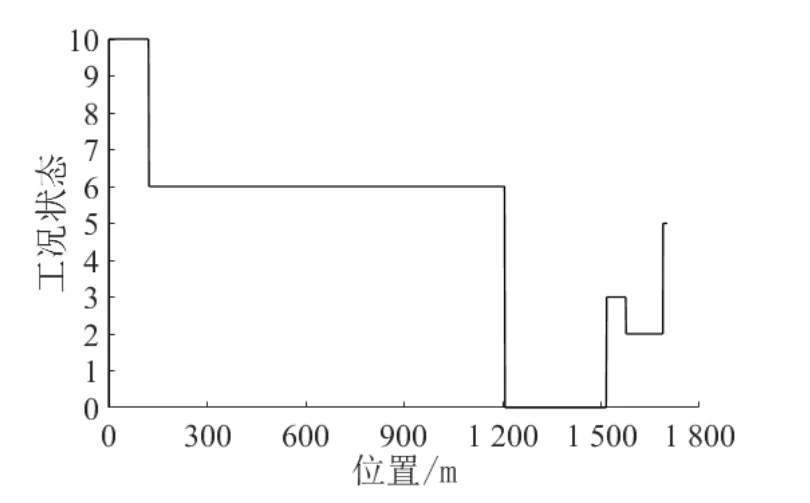
图13 工况距离曲线

图12 是算法生成的最优ATO 速度曲线。图13是工况距离曲线，列车在平坡段施加牵引力加速，然后进行缓慢牵引，在上坡段惰行一段时间，最后施加制动减速停车。在满足区间运行时分的前提下，尽可能地利用了线路优势，减少了牵引能耗。其牵引能耗为28.8 kW·h，较文献7 节能38%。

5 结束语

本文采用多质点模型分析列车运动情况，基于改进的DE 算法，分析线路约束条件，建立评价模型，构建适应度函数，使种群向低能耗、末速度小的方向进行优化。以上海地铁3 号线数据为例，经仿真试验，牵引能耗28.8 kW·h，生成的ATO 速度曲线，在满足定点准时停车的前提下，达到了节能的目标，证明改进DE 算法可用于解决列车节能优化速度曲线问题。但该算法在限速较多的区段，速度曲线计算时间较长，仍需进一步研究和改进。