基于特征综合提取方法的风电机组齿轮箱磨粒分类
苏连成,张光远
(燕山大学 电气工程学院,河北 秦皇岛 066004)
0 引言
在风电机组齿轮箱运行的过程中,内部零件会相互接触摩擦产生磨损颗粒,通过检测齿轮箱油液中的磨粒可以判断磨粒的种类和分布情况,通过对磨粒种类及分布情况的检测就可以判断出风力发电机组齿轮箱当前的运行状况和磨损状态。研究表明大多数机械故障主要是由严重磨损或者有害磨损造成的,因此可以通过对齿轮箱磨粒的检测来判断设备磨损程度和换油时机[1]。
对磨粒类型的判断需要使用图像分析方法来提取分类特征,再通过分类方法进行形状的分类。在过去的20年中,已经提出了许多磨粒图像的分析方法,例如:基本形状因子分析、傅立叶分析和纹理分析[2-8]。文献[2]基于傅立叶特征训练的神经网络根据磨粒轮廓边界曲率信息对磨粒进行了分类,文献[3]基于磨粒的纹理信息特征使用主成分分析和灰色关联分析对严重滑动磨粒和疲劳磨粒进行了区分,文献[4]基于BP神经网络根据磨粒形状、大小和纹理中的7个特征对磨粒进行了分类。现有的研究对磨粒分类的特征选取通常只考虑磨粒的形状信息、轮廓信息或者纹理和颜色信息,很少对几种信息进行综合分析,考虑到本实验样本的主要成分为铁,颜色为黑色,所以在现有研究的基础上综合考虑磨粒的形状特征和边缘细节特征更适合本实验样本的分类。
现有的分类方法大都使用传统的神经网络或者机器学习方法,例如文献[2,4]使用神经网络,文献[3]使用主成分分析法。这些方法只在数据集比较大时才能具有比较理想的识别准确率,当面对较小的数据样本时,分类准确率波动很大。因此,为了更准确地对风力发电机组齿轮箱磨粒进行分类,本文提出了一种综合磨粒边界信息和形状信息的特征提取方法,并使用随机森林算法对特征进行分类,结果表明相比单独考虑形状特征或者边缘特征,使用本文提出的磨粒特征综合选取方法对磨粒进行分类的准确度更高。
1 磨粒图像采集和处理
风力发电机组齿轮箱磨粒的分类具体流程包括:磨粒图像采集、磨粒图像处理、磨粒轮廓提取、形状特征和轮廓特征特征提取、建立分类模型五个部分。分类流程如图1所示。
磨粒分类过程可以分为以下几个步骤:
1) 使用电子显微镜对磨粒图像进行采集;
2) 对采集到磨粒图形进行预处理,通过形态学处理,对磨粒图像进行平滑处理,并去掉图像中由于光线和杂质产生的噪声;
3) 提取图像中所有轮廓,由于本文使用的样本数据大小为75 μm左右,所以可以根据磨粒大小设定周长和面积阈值,对所有轮廓曲线进行面积和周长判断,去掉滤波未去除的较大杂质点,存储符合要求的磨粒图像;
4) 根据对磨粒形状特征和轮廓特征的定义对磨粒轮廓图像进行特征提取;
5) 使用提取的磨粒特征数据对分类模型进行训练。
1.1 图像预处理
磨粒图像通过电子显微镜人工采集,由于磨粒样本中会存在一些杂质而且磨粒表面各个位置的反光度和外界光线也不同,所以在图像中磨粒内部和外部会出现一些噪声干扰磨粒轮廓的提取,通过对图像的预处理可以去除图片中磨粒内部和外部的噪声干扰。磨粒图像的预处理流程包括图像的灰度化处理和平滑处理,处理流程如图2所示。
1.1.1 图像灰度化处理
电子显微镜采集的磨粒图像是三通道的RGB图像,RGB图像能够非常好地反映出磨粒图像的颜色、细节和纹理信息。由于本文只需要考虑图像的形状和轮廓信息,所以只要把磨粒图形转换为单通道的灰度图就能够满足需要,还能够降低程序的复杂度、减少计算量并且提高程序的运行速度。灰度图像的像素值的范围为0~255。灰度图可以根据RGB图像的像素值按照一定规则进行转换。灰度化处理方法为
fgray=0.299fR+0.587fG+0.114fB,
(1)
式中,fR、fG、fB表示原三通道图像像素点的每个像素值,fgray表示变换后的灰度值。
1.1.2 图像的平滑处理
采集好的图像内部会存在很多干扰,例如磨粒外部的杂质点和磨粒内部的高亮点,所以需要使用滤波技术来降低图像内部的噪声和平滑磨粒轮廓以便进行边缘提取。本文采用高斯滤波来消除图像在数字化过程中产生或混入的噪声。高斯滤波是一种线性平滑滤波,可以过滤掉频率较高的噪声又不会对磨粒的轮廓产生过大的影响。其中每一个像素点的值都可以通过对本身和邻域内的其他像素值进行加权平均后得出,权重由高斯函数获得。
由于磨粒图像是离散的数据,所以用到的高斯函数也需要进行离散化处理,高斯函数离散化之后是一个二维矩阵,通过与图像数据进行卷积实现滤波效果,二维高斯函数为

(2)
将二维高斯函数离散化就得可以到高斯核,理论上离散后的高斯核是一个无限的模板,实际上高斯核一般只取距离中心一定范围的离散值,其余部分都为0。本文使用3×3的高斯核,实验表明相比于3×3的高斯核,5×5的高斯核虽然可以过滤掉更多噪声干扰,但是会丢失磨粒的边缘细节,对轮廓点数、周长和面积的提取造成一定影响,因此,考虑到磨粒轮廓信息的准确性,本文使用3×3的高斯核,对于噪声增加的问题会在1.2节进行解决。
平滑化处理后再将图像进行二值化处理为磨粒轮廓提取做准备。图像的磨粒图像的预处理流程如图3所示。
1.2 轮廓提取
将图像进行预处理之后,就需要提取磨粒的轮廓来采集磨粒的边界信息和形状信息。本文采用Canny算子来检测磨粒的轮廓。Canny边缘检测有3个优点:首先使用非极大抑制方法,保留了像素较大的点,具有一定的抗噪声能力;其次使用双阈值法对边缘点进行选取,去除了图像中的假边缘点,具有更高的准确性;最后对边缘像素周围8邻域像素进行检测,判断是否为边缘点,可以获得更连续准确的边缘。图4是使用Canny算子进行边缘检测的效果。
由于滤波时选用了3×3的高斯核,所以难以去除一些面积较大的杂质,在使用Canny算子提取轮廓后,会把磨粒图像外部的杂质轮廓一并提取,所以需要设定一个阈值来筛选符合要求的磨粒轮廓。鉴于本文研究的磨粒大小为75 μm左右,所以在提取轮廓后,对每一个轮廓进行周长和面积的计算,去除掉面积小于50像素或者周长小于300像素的轮廓,通过上述的筛选方法,则可以存储图片中所有的磨粒轮廓。
2 磨粒特征参数
在对磨粒特征进行定义之前,需要对磨粒的中心点坐标进行确定,确定了磨粒中心点坐标,才能得到磨粒轮廓上的每个点的坐标,以便后续进行处理。对于得到的图像来说坐标原点位于图片的左上角,向右为x轴正方向,向下为y轴正方向。轮廓正上方的点是轮廓的第一个点,其他点的顺序以顺时针排列。为了方便后续数据的计算,磨粒的中心使用几何中心(xc,yc),计算方式如下:
(3)
2.1 磨粒边界特征的定义
2.1.1 标准偏差的定义
为了更直观地介绍本文定义的磨粒特征参数,先将参考的磨粒形状简化为椭圆,记为等效分析磨粒,将等效分析磨粒的几何中心作为坐标原点,根据等效分析磨粒的面积计算出椭圆的长短轴长度,并分别以长短半轴长度为半径画出两个分析圆Cmin、Cmax(如图5所示),适当分析等效分析磨粒上的点与Cmax上对应点之间的径向凹面偏差fRCD,就可以评估它们的偏差,基本分析可以如下所述进行:Cmin的半径是从磨粒边界到几何中心的最小距离,而Cmax的半径是最大距离。Cmin和Cmax圆心都与椭圆的几何中心重合。因此磨粒边界上的第i个点Ai的坐标即为(xi,yi),该点对应的fRCD值记为δi,则
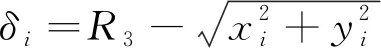
(4)
式中,R3为Cmax的半径,xi,yi为Ai的横纵坐标。
Fig.5 Schematic of wear particlefRCD
对于实际的磨粒图像,可以通过绘制从几何中心到等效分析磨粒和Cmax边界对应点的线段来确定fRCD的值,可以看出fRCD的值δi越小,意味磨粒轮廓上的每个点都与Cmax上对应点的距离越短,即点Ai越接近圆Cmax。
考虑到大多数粒子的形状是不规则的,它们的统计中位数的变化一般代表着不同的轮廓特征。因此,这些值的统计变化对于分析磨损颗粒的形状和类型是有意义的。通常来说,如果中位数接近圆Cmax的半径意味着磨粒形状与圆Cmax的形状非常接近,磨粒的形状更接近圆形。对于局部fRCD值很大的样本意味着磨粒形状很大程度上偏离了圆Cmax,说明磨粒的形状可能不对称或者为水滴形。因此计算这些参数可以有效地分析和识别磨粒的几何形状,并且可以分析出导致这种几何形状出现的齿轮箱运行状态。
如2.1中所述,fRCD值有助于比较和识别磨粒的特征并且能帮助确定磨损的类型,所以统计fRCD值的分布可以为确定磨粒不规则程度提供更完整的信息。在分析fRCD的值δi时,通常将它们的标准偏差σ规定如下:

(5)
其中,i=1,2,…,n(n是磨粒边界点的总数)。
2.1.2 边缘规则度的定义
定义σ与颗粒面积AW的比率为边缘规则度fRDA,根据颗粒形状和轮廓在整体上的异常对磨粒进行分类。fRDA的值越小意味着磨粒的形状和轮廓的异常越小,fRDA求法如下:
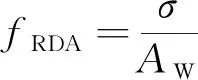
(6)
σ描述了磨粒边缘的不规则度,而fRDA提供了磨粒的形状特征的信息,这两个特征都是用于定量分析磨粒特征的重要参数。但是σ没有考虑到磨粒面积对磨粒边缘不规则度的影响,一个σ比较大的磨粒,边缘通常是较不规则的。但是如果某个磨粒的面积非常小,即使它的σ比较小,也可能有较高的边缘不规则度。所以根据fRDA的定义,这种不规则度可以使用小颗粒的面积AW进一步放大,同样也可以通过大颗粒的面积AW来适当稀释。因此fRDA是一个可以用来衡量磨粒是否规则的参数。当与fRCD结合时,它是评估磨粒的独特特征的另一个有意义的参数。
2.1.3 曲率的定义
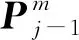
(7)
由图6和式(7)可以看出m的值越大平滑程度越好,但是如果选择较大的m值,则可能无法反映曲线的原始精细特征。另一方面,如果m较小,则不会对曲率的采集产生足够的平滑。因此,为特定样本选择合适的平滑因子非常重要。基本思想是选择对应于由轮廓包围的360°角的固定比例的m值。实验结果表明,两个矢量的起始点之间间隔10°时,求取的曲率是相对优秀的结果,因此,m的值由边界点的数量和36的比值确定。
2.2 形状特征的选取
2.2.1 形状规则度的定义
根据磨粒的轮廓,可由OpenCV提供的库函数拟合得最小斜外接矩阵的4个顶点坐标,由此可计算出最小外接矩形的长Lp和宽Wp,所以为了评估磨粒的面积偏差,定义最小外接矩形和磨粒面积的比值fRCRA为

(8)
由于等效矩形区域Lp×Wp是一个足以包围例子的包络,因此fRCRA的值可以用来确定磨粒和其最小斜外接矩形的接近程度,并且fRCRA的值永远大于等于1。当fRCRA=1时,说明磨粒几乎充满了矩形,所以此时磨粒的形状更接近矩形或规则的细长形。通过引入最大长度与最大宽度的磨粒纵横比fRLW,可以进一步评估磨粒的细长程度。fRLW计算公式为
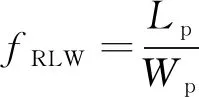
(9)
可以看出fRLW=1时表明磨粒接近正方形或圆形;fRLW>1时表明磨粒更接近矩形。
定义磨粒面积偏差fDWPA计算式为

(10)
式中,A1和A3分别为Cmin和Cmax的面积。
通过对Cmin和Cmax面积的计算,可以反映出磨粒的形状。当A3-AW的值比较小时,意味着磨粒更接近圆形,此时的AW-A1也会比较小。通常来说,fDWPA的值越大表示磨粒更接近细长的椭圆形。
2.2.2 分形维数的定义
分形理论是研究自然界不规则和复杂现象的学科,自相似维数、盒计数维数和Hausdorff维数等都是分形理论中计算分形维数的常用方法,Hausdorff维数能够较精确地计算分形维数,所以本实验采用Hausdorff维数对磨粒的分形维数进行计算。本实验中磨粒的轮廓可以看成单个的不规则岛形图案,根据分形岛的面积周长关系可以得出测定周界分形维数时,其计算方式为
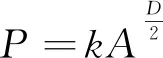
(11)
其中,A为分形岛的面积;P为分形岛的周长;k为尺度常数;D为面积分形维数[8]。
由式(11)可以推导出logP∝logA,因此使用式(11)可以计算单岛的分形维数。当面积一定时,周长越长,则边界越复杂,其分形维数也就越高,如图7所示[9]。
3 基于随机森林算法的磨粒分类实验
3.1 数据集的选取
现阶段的研究[10-13]都会把磨粒类型按照3种方式分类。第一种为按照磨损类型把磨粒分为球形磨损、摩擦磨损、滑动磨损、切削磨损、断裂和严重滑动磨损[13];第二种为根据形成机制把磨粒分为切割磨粒、疲劳磨粒、滑动磨粒和圆形磨粒等;第三种为根据磨粒形状把磨粒分为边缘规则磨粒、边缘不规则磨粒、细长形磨粒和圆形磨粒[15]。前两种通过假设特定的磨损过程会产生何种类型的颗粒来分类的,当仅考虑磨损模式时,这两种假设是正确的。然而机器设备的磨损状况很少只有单一的一种,不同的磨损情况和磨损类型也可能产生相同的磨粒。因此,将磨粒按照几何类型进行统计分类,以便在不同场合中识别磨损模式的方法更适合于大量样本分析。
这四种常见的几何类型即边缘规则磨粒、边缘不规则磨粒、细长形磨粒和圆形磨粒(图8),并且基于这四种几何类型可以把磨粒的形成机制分成摩擦、疲劳、切割和严重粘附。在这四种类型的磨粒中,规则和不规则描述磨粒轮廓或边缘,圆形和细长主要代表磨粒的几何形状,它们的情况反映设备的磨损状况。表1总结了现有文献[5,13-15]中按照上述参数规定的磨粒的几何分类情况,该表把磨粒的几何形状和特征与其磨损类型相关联,并阐述了可能出现的磨损类型、形成机制和预期的设备维护操作。
本文按照上述规定建立了一个风电机组齿轮箱磨损颗粒的数据库,包含495个磨粒图像样本,其中边缘规则磨粒212个,边缘不规则磨粒156个,细长形磨粒45个,圆形磨粒82个。将其用为本实验中的分析对象。通过式(1)~(11)分别测定周长、面积、曲率、fRCD、σ、fRDA、fRCRA、fRLW、fDWPA和分形维数等特征。为了证明所提出的特征综合提取方法能够提高风电机组齿轮箱磨粒分类的准确性,本文将实验样本分为3组:组1单独考虑磨粒的形状信息,包含周长、面积、σ、fRDA和曲率5种特征;组2单独考虑磨粒的边缘信息,包含周长、面积、fRCRA、fRLW、fDWPA和分形维数6种特征;组3综合考虑磨粒的形状信息和边缘信息包含全部的9种特征。每组数据包含495个磨粒样本,其中397个用来训练随机森林模型,98个用来测试模型的识别准确率。
3.2 随机森林算法原理
随机森林是通过集成学习的思想将多棵决策树整合成森林的一种算法,它的基本单元是决策树,它的本质集成学习方法属于机器学习的一个分支。同时随机森林又是一种Bagging思想,对于一个输入样本,森林内部的N棵树会产生N个分类结果,随机森林继承了所有的分类投票结果,将投票次数最多的类别指定为最终输出,所以它的准确率要比传统决策树更高。本文根据随机森林的这一特点,建立模型的过程如下:
1) 对于大小为N的训练集,对于森林内的每棵树而言,随机且有放回地从训练集抽取N个训练样本作为该棵树的训练集;
2) 如果每个样本的特征维度为M,则制定一个常数m≪M,随机地从M个特征中选取m个特征子集,每次树进行分裂时,从这m个特征中选择最优的;
3)每棵树都尽最大程度生长,并且没有剪枝过程。
通过随机抽样和随机选取特征值使随机森林不容易陷入过拟合并且有良好的抗噪能力。Gini指数又称Gini不纯度,表示样本集合中随机选中的一个样本在子集中被分类错误的概率,本文使用Gini指数作为衡量标准计算特征重要性,节点m的Gini指数为
(12)
式中,K为类别个数,pmk为节点m中随机选取一个样本属于k类别的概率[18]。计算出来后,选择Gini指数最小的那个特征作为最优划分特征。特别的当Gini指数为0时,表示一个节点中所有样本都属于同一个类别。

表1 磨粒形状/轮廓类型、磨损模式和磨损严重程度的相关性Tab.1 Correlation of wear particles shape/contour type, wear pattern and wear severity
3.3 仿真实验与结果分析
本实验使用PyCharm搭配sklearn库,通过调用sklearn库中的RandomForestClassifier函数来完成随机森林分类模型的构建,RandomForestClassifier函数中参数n_estimators为每个模型中决策树的数量,本实验中将n_estimators设定为200,分别使用3组数据建立随机森林分类模型,每组模型分别训练500次,得到每组数据的实验次数和准确率的关系如图9。
图9中,绿色星形线为第一组只考虑边界特征的分类准确率;蓝色虚线为第二组只考虑形状特征的分类准确率;红色实线为第三组综合边界特征和形状特征的分类准确率。可以看出,第三组数据的准确率波动最小且准确率最高,平均准确率可达到85.52%,因此综合考虑磨粒的边界特征和形状特征能有效提高磨粒识别的准确率。
同时测试集的98个磨粒中分别包含边缘规则磨粒32个、边缘不规则磨粒31个、细长磨粒12个和圆形磨粒23个。使用第三组数据的训练集进行建模,对测试集标签进行检测,在一次整体准确率为85.75%的实验中,得到检测磨粒样本的标签情况,如表2。

表2 随机森林算法检测结果Tab.2 Forecast results of random forest algorithm
表2中,横向为对某种磨粒的检测结果,例如使用模型对边缘规则磨粒的特征进行检测,检测结果中有27个边缘规则磨粒、2个边缘不规则磨粒、0个细长磨粒和3个圆形磨粒。因此从表2中可以看出,模型对细长磨粒的识别准确率最高,达到100%,对边缘规则磨粒、边缘不规则磨粒和圆形磨粒的识别准确率分别为84.38%、83.87%和82.61%。可以看出使用本文所提出的磨粒特征选取方法可以有效地提高对磨粒类型的识别率,为后续根据磨粒种类确定设备运行状态提供了很大帮助。
4 结论
本文根据相关图像处理方法和随机森林算法研究了风电机组齿轮箱的磨粒分类问题。首先通过图像处理的相关方法得到了磨粒的轮廓信息;随后通过选取磨粒的边界信息和形状信息确定了周长、面积、曲率、σ、fRDA、fRCRA、fRLW、fDWPA和分形维数9个特征参数,基于定量分析和实验结果,证明这些特征参数能够用来区分磨粒的特征和类型;最终采用随机森林算法根据磨粒的形状和轮廓分为4类,即边缘规则磨粒、边缘不规则磨粒、细长形磨粒和圆形磨粒,通过对比其他数据选择方法,表明综合分析磨粒的形状特征和轮廓特征可以更准确地识别磨粒的类型。本文提出的综合特征选取方法在风电机组齿轮箱磨粒分类的问题上确实有效,为以后分析风力发电机组齿轮箱的运行状况及设备维护提供了重要帮助。

