社会化媒体营销下的生鲜电商库存决策研究*

□ 乔梓钰，兰洪杰

(北京交通大学 经济管理学院，北京 100044)

随着互联网的快速发展，越来越多的传统生鲜零售企业转向线上发展新零售，电商之间竞争日益激烈。为了增加销量提高利润，电商需要采取不同的营销手段为商品引流，流量是衡量电商生意的重要指标之一。

社会化媒体营销作为现代营销工具，可以显著提升商品流量。它是指运用社会化媒体如博客、微博、社交工具、社会化书签、共享论坛，来提升企业、品牌、产品、个人或组织的知名度、认可度，以达到直接或间接营销的目的[1]；其因具有全民性、互动性、精准性等显著特点被各个行业广泛使用，但因营销的时效性问题，社会化媒体营销带来的预估销量无法具体量化，导致零售商备货时可能面临着备货不合理现象的发生：具体表现为营销效果较差而产生的库存剩余和营销效果较好产生的备货不足，特别是对于以乳制品为例的生鲜品类来说，低温乳品生命周期短，温控要求高，库存周转要求快速，这就需要对客户订单有精准的预估，预判越是精准其库存越接近零库存，从而越能够降低成本。不合理的库存管理会产生巨大的库存持有成本和缺货成本，直接影响电商的整体利润，因此，如何在社会化媒体营销方式下优化库存决策对生鲜电商有很强的现实意义。

1 文献综述

现有学者对社会化媒体营销的研究多是对消费者购买意愿及产品销量的影响，与库存管理结合的较少。然而在现代交易环境中，研究营销方式对库存策略和需求的影响是有必要的，因为营销方式会直接影响消费者购买决策，从而影响需求分布，而库存决策往往是基于一定的需求预测做出的。在考虑营销因素的库存研究中，李富昌(2016)在考虑营销成本条件下，建立库存与运输联合优化(ITIO)三阶段决策模型，根据求解的模型性质对库存、成本进行决策[2]；张廷龙(2010)在由一个供应商和一个销售商构成的两级分布式供应链结构中，考虑广告投入影响需求时渠道回扣契约与供应链协调[3]；田进凤(2016)将订货提前期及顾客需求考虑为不确定的正态分布，通过模糊理论确定模型中的不定值，最终建立三级供应链的多目标库存模型，从而计算出最优解[4]；叶善文(2019)结合近年来双渠道供应链库存策略的研究，分析如何在双渠道营销模式下做好制造商库存管理工作，以此改善整体供应链的库存管理水平[5]；夏海洋和黄培清(2010)通过算法建模分析了需求对营销投入敏感性的变化以及商品退化率对系统最优策略和利润的影响。针对退化性商品联合制定库存决策及营销决策以使供应链效率达到最优[6]。

纵观以上研究，未有社会化媒体营销与库存结合的文献。社会化媒体营销作为现代营销的重要方式，Cheung ML等(2020)使用偏最小二乘结构方程模型(PLS-SEM)测试社交媒体营销元素，消费者品牌参与度和品牌知识之间的联系[7]；Yao B等(2019)利用二元logit模型和区间截尾回归来检验社交媒体营销在绿色产业中的用途和影响。结果表明社交媒体营销能够使公司获得较高的销售回报[8]；李锋等(2017)在WS模型的基础上构建了具有小世界网络特性的社交网络，运用报童模型分析网络营销情景下迭代产品的需求变化、风险控制和库存管理问题[9]。

本文在原有研究的基础上，选取乳业电商为研究对象，构建社会化媒体营销和库存联合决策的多周期动态规划模型，并利用K-Means聚类辅助数值实验进行求解；同时，为采购成本较高、对零售商利润影响明显的商品建立基于长短时记忆网络(Long Short Term Memory，LSTM)神经网络的需求预测模型，输入历史销售量数据，利用Leaky ReLu作为非线性激活函数，使用Adam算法作为监督学习的训练优化器，进而更精准的提供库存优化建议。

2 问题描述与模型建立

本文以奶类生鲜电商为主要研究对象，探究其在现代网络环境中，采用短视频、微博、社区论坛等社交媒体进行宣传和推广，增加商品流量，从而使“潜在客户”转化为实际购买商品的客户这一营销行为及其库存决策问题。采用社会化媒体营销可以有效提高转化率，即零售商可通过社会化媒体营销这一方式，提高用户对于低温液体奶的需求量。故在每个销售周期开始时，零售商需要针对社交媒体营销投入量及库存持有量进行优化研究，使本销售期所获利润最大。低温液体奶保质期短、温控严格、库存周转率高，对此类商品进行营销及库存联合决策十分必要。但基于市场不确定性，社交媒体营销投入量及库存持有水平的决策一直是一大难点，很容易因为库存决策不准导致乳品变质，造成大量浪费和利润损失。本文通过建立数学模型描述这一实际问题，利用K-means聚类对不同种商品进行聚类实现对不同类商品的参数确定，进而得出在特定情况下应投入社会化媒体营销的相对量及库存持有量。对于生产成本较高的商品，使用历史数据训练LSTM模型，进而达到更为精准的预测量级，为商家提供更加合理的联合决策建议。

2.1 符号与假设

本文在后续建立模型及求解模型部分使用的符号及其对应含义如下。

表1 文中所用符号及其含义

本文在考虑实际中企业经营状况、库存及进货情况的同时，尽量简化模型，算例分析时考虑仅涉及一种商品，一家零售商，而零售商也仅向一个供应商采购商品，故做出以下合理假设：

①在T期内，商品的采购成本、销售单价及社交媒体营销成本保持不变；

②在本文t期内，缺货不补。即当顾客需求量大于总库存量时，零售商不进行补货。

③在T期顾客总需求保持不变；

④各项单位成本以及固定成本不随时间发生变化；

⑤库存产品的价值不折损，即t期库存大于0时，t+1期商品价值不变；

⑥每次从供应商进货的等待期为0，即不考虑特殊情况如极端天气等不稳定因素的影响；

⑦顾客需求的期望在一定范围内与社交媒体营销的投入成正相关。

2.2 模型建立

由假设部分③可知研究期内顾客对商品的总需求不变。在本文中，将研究期T划分为3个子研究期t1、t2、t3，即t1+t2+t3=T。根据实际情况，各个子研究期的需求分布为随机分布。考虑到研究初期且不失一般性，故将随机需求函数定为加式需求，计算式如下：

上式中，a为加式需求的系数，ε为均值为0的随机变量，使需求具有随机性。社交媒体营销的投入越大，产生的网络曝光量越大，故每个子研究期的顾客需求随之增加，即每个子研究期的需求均值会受社会化媒体营销影响，如下式所示：

上式中明显可见，每个子研究期需求均值不会高于研究期的市场总需求。α(g)体现为研究期内社会化媒体营销对需求的影响因子，在一定范围内，社会化媒体营销投入量越大，其对顾客需求的影响越大。

根据上述推导与符号含义，可得如购进充足商品时，t1、t2、t33个子研究期所获的利润如下：

P1=(w-c)r1-k1-s(x-r1)
P2=(w-c)r2-k2-s[x-(r1+r2)]
P3=(w-c)r3-k3-s[x-(r1+r2+r3)]

即购进充足商品时，总利润表达如下：

由上述推导可知，总利润可用下式计算：

P=(w-c)[μ1+α(g)(r1-μ1)+aε]-k1-s[x-μ1-α(g)(r1-μ1)-aε]+(w-c)[μ2+α(g)(r2-μ2)+aε]-k2-s[x-μ1-α(g)(r1-μ1)-aε-μ2-α(g)(r2-μ2)-aε]+(w-c)[μ3+α(g)(r3-μ3)+aε]-k3-s[x-μ1-α(g)(r1-μ1)-aε-μ2-α(g)(r2-μ2)-aε-μ3-α(g)(r3-μ3)-aε]

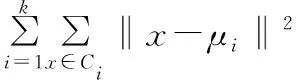
2.3 算例分析

根据上文所述，使用K-means算法对商品进行聚类便于针对商品不同现状进行定制化营销。由于其簇值K较难确定，故使用肘部算法依据簇内误方差进行确定。将顾客在商品宣传界面平均停留时长及商品成交转化率作为聚类依据，肘部算法结果图如图1所示。

图1 肘部算法确定K值

根据上述聚类结果图，可见聚为3类更加合理。可理解为对应3种情况：①营销较好且销售情况较好；②营销较好但销售情况欠佳；③营销欠佳且销售情况欠佳。针对①②中情况，α(g)影响因子曲线应更加平缓，针对③中情况，α(g)影响因子曲线应更加陡峭，表现为具备营销潜力。

为了说明此模型的实际应用效果，本文在单研究周期内以某款低温乳品商品进行数值实验。其每单位进价为15元，售价19.9元，根据聚类可知其营销状况欠佳且销售情况欠佳，具备营销潜质。在此基础上对此商品投入社会化营销，影响因子α(g)按上述规则设置，初始库存水平设置为2100、2300、2500。按如上模型进行数值实验，结果如下表2所示。

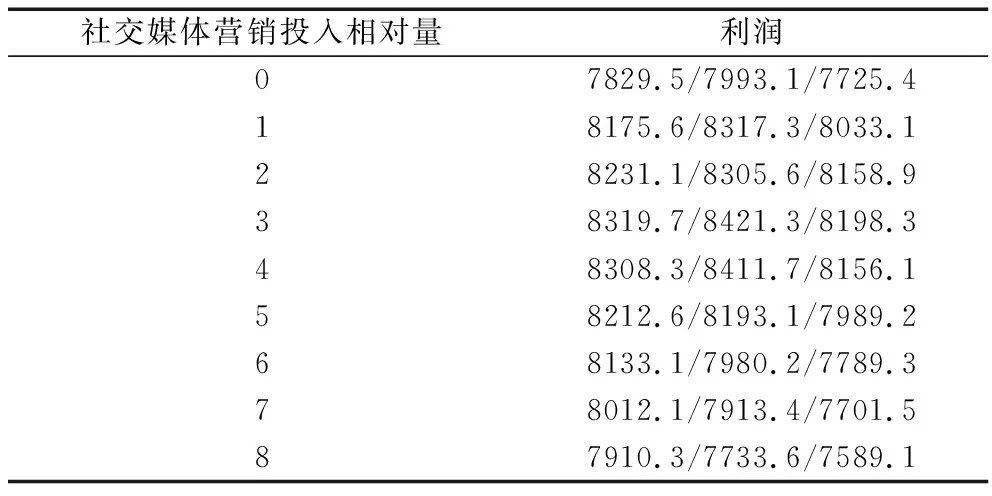
表2 数值实验结果表

由表2可见，某一研究期的利润为库存及社交媒体营销投入量的凹函数，利润先随着社交媒体营销投入量及库存水平升高而增加，经过极值点后便开始减小。由于社交媒体营销及库存存在成本，当二者量过大时，因二者所产生的利润无法弥补二者的固定成本。

由表2可知，当投入3单位社交媒体营销且初始库存为2300单位时，获得利润最大。该数值实验为实际中的一种可能情况，即投入社交媒体营销带来的净利润为正数，可在一定程度内投入社交媒体营销。当实际中选用不同货物时，即按情况修改售价、进价等超参数即可。

在模型实际应用中，通常会采用与本文数值实验不同的参数。为了验证以上模型对不同参数的适应情况，在此部分进行模型对各参数的灵敏度分析实验。大幅度改变售价及社交媒体营销因子验证模型性能，得到结果如图2所示。

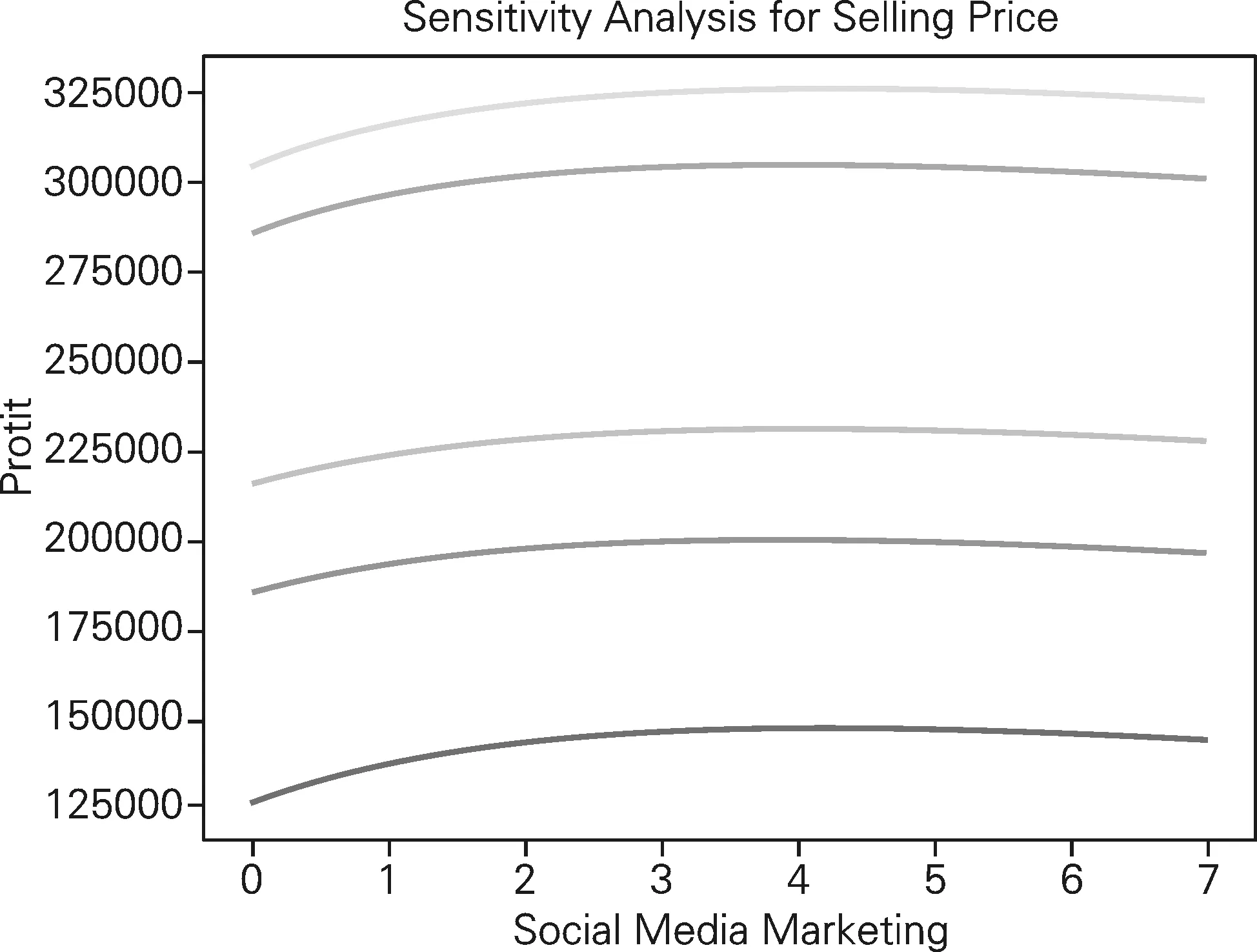
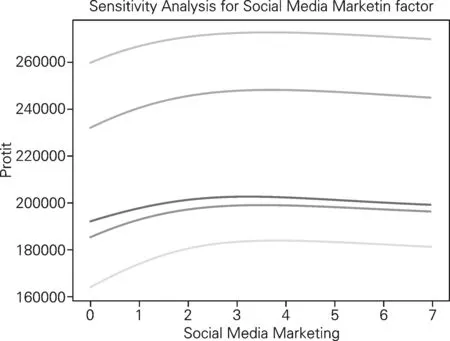
图2 模型对商品售价及营销影响因子的灵敏度

由图2可见，当改变售价及社交媒体营销因子时，模型求解曲线整体形状不变，说明本文提出模型对售价、社交媒体营销影响因子具有较强的鲁棒性，对不同场景下不同数据均具有较好的适应能力。

3 LSTM预测

根据算例分析部分可见，上述模型对方程参数具有鲁棒性。但仍会存在隐含小范围误差的风险。针对高成本商品，即使小范围的误差也会对利润产生较大影响，故此类商品在库存决策方面应尽可能减少误差。针对于此类商品，利用历史数据训练销量预测模型，使其达到精准预测。循环神经网络(Recurrent Neural Network，RNN)将当前时刻的输出作为输入流入下一步，可捕捉时间序列内部的关联性，对信号具有一定的记忆能力，因此，在时序相关数据预测方面取得了优异效果。但在传统RNN结构中，反向传播计算梯度时采用链式求导法则，即总梯度的计算公式为许多梯度值连乘的形式，一旦出现小于1的梯度值，累乘结果会越来越小直至消失，导致参数更新停止，致使网络丧失记忆能力，即梯度消失现象。为解决这一问题，本文采用LSTM对销量进行预测，其通过引入门结构，对网络中记忆状态进行保护，克服传统RNN劣势。典型LSTM结构图如图3所示。

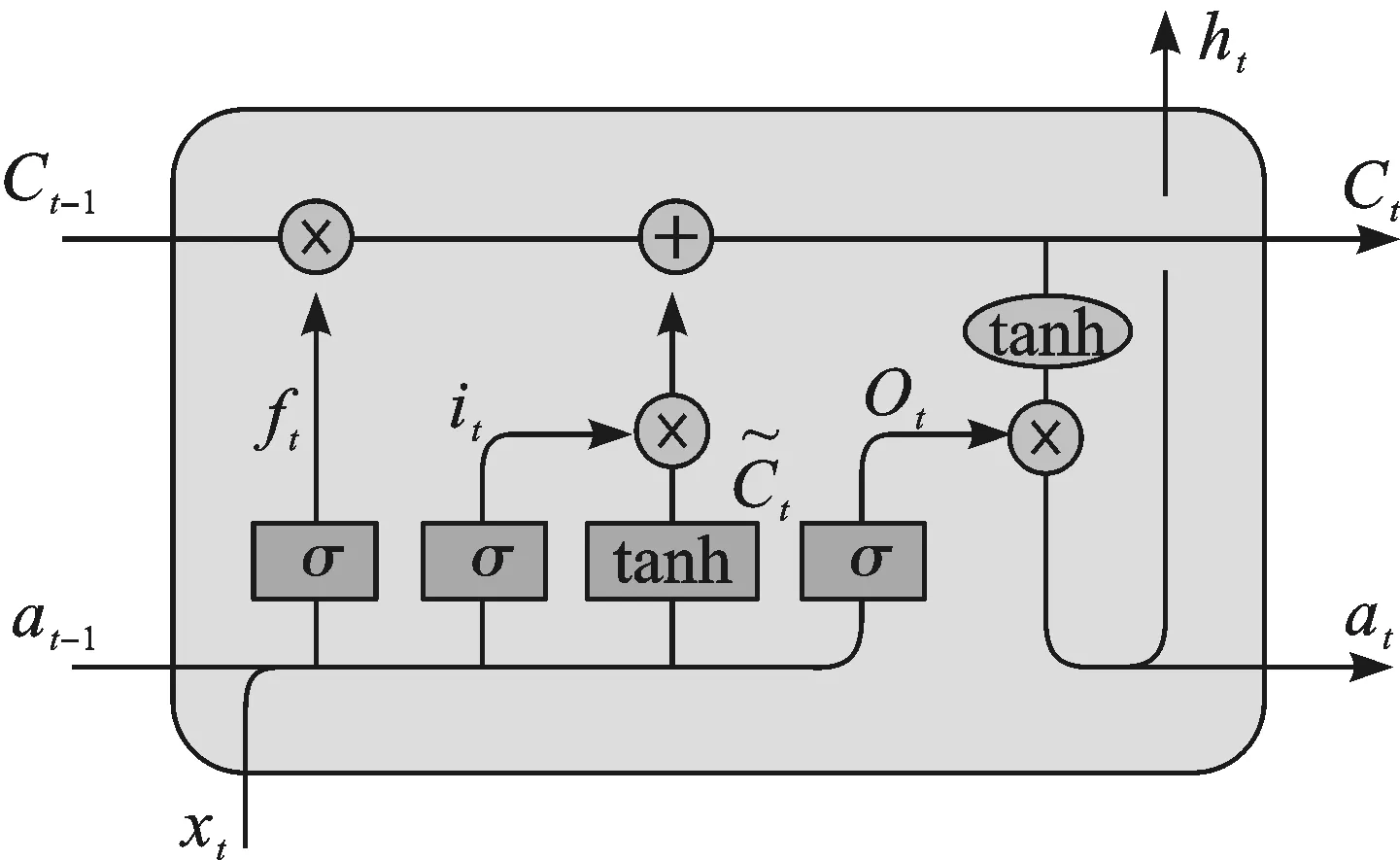
图3 典型LSTM结构

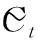
3.1 数据标准化

通过对训练数据分析可知，由于促销活动等因素，数据存在较大波动。如直接输入LSTM训练时会导致反向传播时变化幅度过大从而影响训练效果。故在训练前需对数据进行预处理，本文对Max-Min标准化及Z-Score标准化进行实验，二者计算公式如下。

由上可见，前者对原数据采用减最小值并除最大差值的方式，使新数据值域为[0，1]，后者对原始数据采用减均值并除标准差的方式，降低原始数据波动程度。

3.2实验过程

此部分实验环境基于Python3.7，Tensorflow2.0框架，训练数据与测试数据比例为8：2，其中LSTM隐藏层结点设为40，训练优化器采用Adam，损失函数采用均方误差(MSE)，设置学习率为0.01，循环迭代训练400epoch。针对3.1部分数据预处理方式及非线性激活函数选择，本文依据测试集MSE为依据进行选择，实验结果如表3所示。

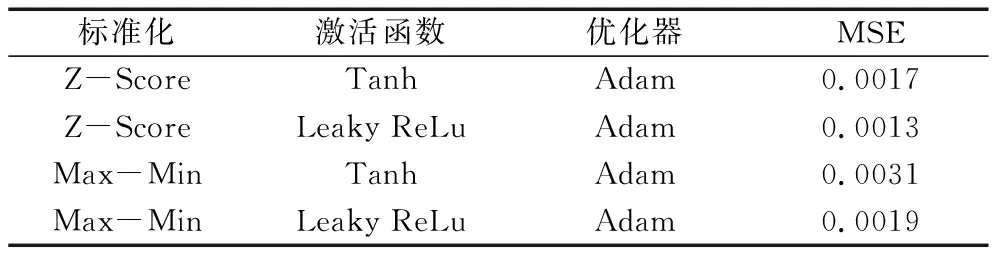
表3 LSTM实验

由表3可知，对数据进行Z-Score标准化并选用Leaky ReLu作为非线性激活函数对应误差最小。其在测试集上预测结果如图4所示。

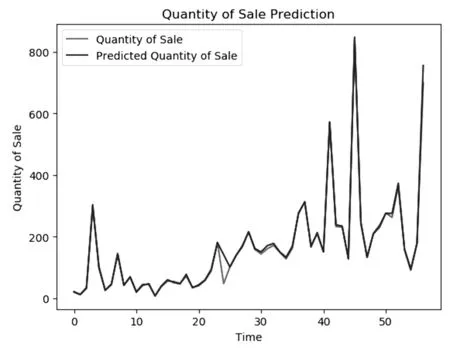
图4 LSTM销量预测结果图

由图4可见，训练所得模型对大幅度波动数据预测效果优异，可实现对销量的小误差预测，具有实际应用价值。

4 研究结论

本文研究对象为生鲜乳品，良好的需求预测能够精简库存，保证社会化媒体营销下的销售情况稳定。本文运用K-means聚类分析和改进报童模型，确定了所需研究商品类的最优订货量和社会化媒体营销投入量；同时，针对高价值商品采用长短时记忆网络精准预测需求量。根据算例分析部分数值实验及实验过程部分LSTM结果预测可知，商家在进行社会化媒体营销和库存联合决策时，要根据商品的属性、成本、售价等因素决定其临界点，从而保证电商总体利润最优，对于生鲜电商的库存和营销联合决策有较强的参考意义。