群智能优化算法在图像分割中的应用

王玉银

（桂林理工大学博文管理学院，桂林541006）

0 引言

图像分割是指从图像中提取出需要的目标，使得背景与目标分离。目前阈值分割法主要有最大类间方差法、二维灰度直方图的投影阈值法、最小交叉熵法、正态分布假设下的最小误差阈值法等。其中最大类间方差法是通过计算阈值t 将平面分为两部分，一部分是阈值低于t 的集合，一部分阈值高于t 的集合，从而得到二值化图像。最大类间方差法因其计算方法简单、速度快，被广泛应用于图像分割中。

近年来，人工智能的快速发展，越来越多的智能优化算法为解决图像分割提供了新的思路，例如粒子群算法、狼群算法、鸽群算法、萤火虫算法、遗传算法等对图像进行分割，而且相对于直接使用最大类间方差法或者聚类方法等，在图像分割的准确率、运算速度和收敛速度方面均有一定程度的提高。群体智能算法能够有效地解决非线性优化问题，因其收敛速度快、算法原理简单易实现、效率高等特点，引起许多研究者的关注，从而得到广泛应用。因此本文针对新的群体智能算法--海鸥优化算法，并结合OTSU 法将其应用于图像分割中，实验证明，该算法能够较好地实现图像分割。

1 海鸥算法

海鸥是最常见的海鸟，经常成对或成小群活动，或者在空中飞翔。海鸥是一种攻击力极强的动物，经常盘旋在空中凭借智慧来寻找和攻击猎物，海鸥会随着季节变化在不同区域之间迁移，以寻找最丰富的食物，从而提供足够的能量。海鸥在迁徙时，经常会攻击候鸟，在攻击时，群体做出螺旋自然运动形状。因此海鸥的两个最重要的特征是迁徙和攻击行为。海鸥的迁移和攻击猎物行为与优化目标函数类似，在给定的搜索空间中搜索最优解。

1.1 迁移

海鸥的迁移过程相等于全局搜索，根据迁移规则中的解决方案来找到当前最佳海鸥所在位置。在迁移过程中，海鸥需满足以下三个条件：

（1）避免碰撞

迁移时，每个海鸥的位置不同。为了避免邻居（即其他海鸥）之间的碰撞，使用附加变量A 来计算新的海鸥位置。

Cs(x)表示海鸥的新位置，该位置与其他海鸥不冲突。Ps(x)表示当前位置，x 表示当前迭代次数，A 表示在搜索空间中海鸥的运动行为，A 的范围为[0fc]。

fc可以控制变量A 的频率，它的值从2 线性降低到0。

（2）最佳位置方向

向最佳位置方向靠近：海鸥在迁移过程中，会向最佳位置方向移动。

Ms(x)表示最佳位置所在的方向，B是负责平衡全局和局部搜索的随机数。

B=2×A2×rd（4）rd是[0，1]范围内的随机数。

（3）接近最佳位置

接近最佳位置：海鸥向着最佳位置的所在方向移动，到达最佳位置。

Ds(x)是海鸥的新位置（最佳位置）。

1.2 攻击

海鸥的攻击行为相当于局部搜索，海鸥在迁徙过程中用翅膀和重量保持高度，不断改变角度和速度进行攻击。在攻击猎物过程中，保持螺旋形状运动。在空间x、y 和z 平面中的运动行为描述如下：

其中r 为螺旋的半径，α是[0，2π]范围内的随机值。u 和v 是螺旋形状的相关常数，e 是自然对数的底数。

海鸥的攻击位置由公式（10）计算得到。

Ps(x)表示海鸥的攻击位置，也就是搜索空间的最优解。

2 二维最大类间方差法（二维OTSU）

由于一维灰度直方图对于有噪声干扰的图像分割性能方面有所下降，一维灰度直方图不一定存在明显的波峰和波谷，因此在一维直方图的基础上，引入图像的邻域平均灰度值即构成二维灰度直方图，既考虑了图像的像素信息也考虑了图像的空间信息。二维最大类间方差法是采用像素点灰度值和其邻域像素的平均灰度值来计算阈值。二维灰度直方图（图1）中，若（s，t）为分割的阈值点，则二维直方图被分为四块，如图1所示。

图1 二维灰度直方图

绝大多数情况下，图像背景与目标的边界附近的像素点有明显的差异，对应的二维直方图为对角线的上的区域为目标（C0）和背景（C1），远离对角线的区域（C2和C3）为边缘或者噪声。

令P(C0)表示目标C0(s,t)的概率，P(C1)表示背景C1(s,t)的概率。则：

目标与背景对应的均值矢量分别为：

二维直方图上总的均值矢量为：

区域c2和c3表示目标和背景的边界信息。远离对角线的边界信息通常忽略不计，即区域i=s+1,…,L-1和j=0,…,t或者i=0,…,s和j=t+1,…,L-1 的概率和约为0，pij≈0。

所以：

类间的离散度矩阵表示为：

使用SB的迹作为类间的离散度测度：

最佳阈值(s*,t*)则由式（20）确定：

二维OTSU 算法是由图像像素灰度值与邻域平均灰度值构成，可以提高计算阈值的准确性和算法的抗噪能力，但是计算量却较大。在任一点（s，t）处计算SB的迹trSB（s，t），对均值矢量和概率都是从原点（0，0）开始重复计算相应项的累积和。因此本文计算OTSU 采用景晓军等[1]提出的快速递归算法计算目标和背景的距离测度来获取最佳阈值。采用快速递归算法能够减少计算时间以及所需的空间。

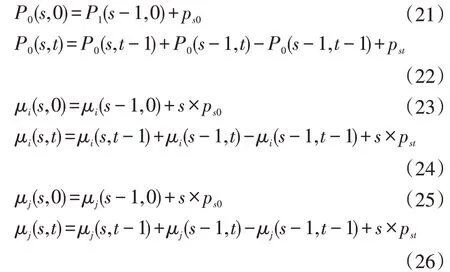
3 基于海鸥算法的图像分割技术

海鸥算法是Dhiman G 等人[2]提出的模拟自然界海鸥寻找食物的过程来寻求最优解。海鸥算法作为一种新的迭代优化方法，将每只海鸥的位置作为空间的解，最丰富的食物所在位置为最优解，海鸥不断地迁移和攻击来寻找丰富的食物。二维最大类间方差法在本质上是对图像在二维灰度空间中搜索最优解，使得目标函数获得最大值，计算量比较大，因此将海鸥算法应用于最大类间方差的图像分割中，可提高算法的效率。

基于海鸥算法的图像分割技术实际上是根据图像的灰度直方图信息，对海鸥算法进行初始化，使用类间的离散度测度作为适应度函数，对海鸥进行迁移和攻击操作，实现群体不断更新，使得群体中的个体不断进行优化，最终获得最大类间方差的最优分割阈值。海鸥算法的描述步骤如下：

（1）参数初始化。设置海鸥最大迭代次数MAXiteration、频率变量fc、螺旋形状的相关常数u和ν、rd以及θ。

（2）计算附加变量A（公式2）、负责平衡全局和局部因子的随机数B（公式4）

（3）根据适应度函数公式（公式19-26）求解每只海鸥的适应度的值Ps(x)和海鸥的所在位置Cs(x)（公式1）。

（4）将海鸥的迁移位置，步骤（3）中求解出来的适应度函数进行比较，从而找到比较好的位置Pbs(x)，根据海鸥的初始位置和较好位置得到较好位置所在方向Ms(x)（公式3）以及最佳位置Ds(x)（公式5），更新海鸥的适应度值和最佳位置。

（5）通过海鸥攻击半径r，计算攻击位置坐标，根据海鸥的位置、攻击半径、攻击方向坐标和最佳位置更新海鸥新的位置Ps(x)（公式10）。

（6）重复执行步骤3、4、5 更新海鸥位置。如果找到最佳位置停滞且不再发生变化，就终止此过程，否则转到步骤3 继续执行，直到达到最大迭代次数而停止。

（7）利用得到的最佳阈值Ps(x)对图像进行分割。

4 实验结果与分析

海鸥算法倾向于探索不同的较好的区域空间。在初始生成过程中，搜索区域变化较快。在迭代的初始步骤中，海鸥算法由于其自适应机制，收敛速度更快。为了验证本文算法的合理性，对coin 图像进行实验，图片的分辨率为512×512。实验环境为：Windows 7 操作系统、程序运行软件为：MATLAB 2016b。参数设置为：频率变量fc=2，螺旋形状的相关常数u=1，ν=1，Max_iterations=200，rd为[0，1]范围的随机数以及θ取（0，2 π）的随机角度值，其中搜索空间维数为2。

分别采用OTSU 算法和海鸥算法对图像进行分割，得到的分割效果如图2 所示。

图2 图像分割结果

从图2 图像分割结果中，可以看出本文算法分割的结果较OTSU 算法分割的结果更抗噪性，例如coin图像边缘部分分割中有一些改进。另外本文算法在对图像coin 分割时所需运行时间为0.988411 秒，而二维OTSU 算法所花费的时间为1.394627 秒。相比来说，海鸥算法有较好的分割结果以及较短的分割时间。

5 结语

本文主要采用群智能优化算法——海鸥算法进行图像分割，实验中对coin 图像实现了分割，并采用对比算法OTSU 算法来验证本文算法的优越性。从总体来看，这两种算法都可以对分割图像的轮廓展现出来。而在抗噪性和时间方面，海鸥算法都有一定的优势。实验结果表明，海鸥算法不仅能够获得二维OTSU 算法相当的分割结果，而且运算时间较短。因此，将海鸥算法应用图像分割中，可有效提高寻优能力，同时运行时间更短。在图像分割处理中，本文算法具有更好的实用价值。