结合未标签样本和CNN的高光谱遥感图像分类

韩彦岭，高仪，王静，张云，洪中华

(上海海洋大学 信息学院，上海 201306)

0 引言

高光谱图像(hyperspectral image，HSI)通常由数十至数百个相同场景的光谱数据通道组成，实现了遥感数据图像维与光谱维信息的有机融合，即在获得地物目标二维空间图像信息的同时，还可以获得表征其物理属性的高分辨率光谱信息，具有“图谱合一”的特性。因此，高光谱遥感数据被广泛应用于农业[1]、对地观测[2]和环境科学[3]等领域。在上述应用中，通过对高光谱图像进行像素级分类是其中的重要技术环节[4]。由于光谱和空间结构的复杂性、高维性以及有限的训练样本问题，高光谱图像的分类仍然是一项具有挑战性的任务。

由于高光谱遥感图像数据包括不同波段的图像，针对图像中每一像素都可以获得对应连续的光谱曲线，不同地物的光谱曲线也有所不同，因此传统的高光谱图像分类技术大多只利用了图像中的光谱信息，如K近邻(K-nearest-neighbors， KNN)、支持向量机(support vector machine， SVM)、罗杰斯特回归(Logistic regression， LR)等。为了充分利用高光谱图像中的空间信息，需要通过一定的提取方法来更好地表征空间特征[5]，如Su等[6]提出了一种基于灰度共生矩阵(gray-level co-occurrence matrix，GLCM)纹理分析的渤海海冰检测方法。Imani等[7]通过GLCM、Gabor滤波(gabor filtering)和形态学轮廓(morphology profiles， MPs)从相邻像素中提取空间信息，研究空间特征与光谱特征的不同组合。其中，基于统计学的GLCM算法由于其提取的特征维度小、鉴别能力强，且具有较强的适应性和鲁棒性，从而引起了人们的关注[8]。研究表明，引入空间信息能够有效地弥补单独使用光谱信息的不足，但是目前基于专家经验和先验知识所提取的浅层手工特征的方法往往忽略了深层特征，而且所提取的特征对于其他数据集的普适性也存在疑问，从而限制了高光谱图像分类精度的提升。

近几年，深度学习模型在计算机视觉领域获得了较好的发展。由于其由浅层到深层、由简单到复杂进行学习的特性，被广泛地应用到遥感领域。在2014年，Chen 等[9]在遥感领域首次提出了一种基于深度学习的高光谱图像分类方法，利用堆叠式自动编码器(stacked auto-encoder， SAE)提取高光谱图像的层次特征和鲁棒性特征。Hu等[10]采用深卷积神经网络(deep convolutional neural network， Deep CNN)直接对光谱领域中的高光谱图像进行分类。Chen等[11]针对深度学习的优点，利用三维卷积神经网络(3D-CNN)提取高光谱图像的光谱空间特征。Zhao等[12]提出了一种基于光谱空间特征的分类框架，该框架分别利用平衡的局部判别嵌入(local discriminant embedding， LDE)算法和CNN进行光谱特征提取和空间特征提取。2017年， Li等[13]提出了更轻量、更易训练的3D-CNN模型，有效地提取了深空谱组合特征。Chen等[14]提出了一种将Gabor滤波器和卷积滤波器相结合的高光谱图像分类方法。Gao等[15]将从原始图像中提取的各种特征作为输入，结合CNN和多特征学习建立新的高光谱图像分类框架。其中，CNN作为一种局部连接网络，通过卷积核从输入数据中自动地学习具有平移不变性的特征，将表示的特征与对应类别结合起来进行联合学习，同时对特征进行自适应调整，获得最佳的特征表示。而高光谱数据通常以三维数据立方体表示，契合了CNN中的三维卷积滤波器提取特征的输入方式，为同时提取空谱联合特征提供了简便有效的办法[13]。

基于以上研究，考虑到单独使用空间信息或光谱信息的局限性，本文提出一种基于GLCM和3D-CNN的空谱联合特征的高光谱遥感图像分类方法。利用原始高光谱图像，结合GLCM算法提取的相关纹理特征，并通过近邻未标签样本的信息进一步增加标签样本信息的多样性，最后利用三维卷积神经网络进行深层次空谱特征的联合提取，用于高光谱遥感图像的像素级分类，可以获得更高的分类精度。在高光谱遥感数据上的实验结果表明，相比其他方法，本文建议的方法具有更好的分类性能。

1 分类方法

1.1 本文高光谱图像分类框架

本文建议的方法主要思想是利用手工提取的地物纹理特征增强样本的空间特征，并融合标签样本及其近邻未标签样本，以增加样本信息的多样性，在较少的训练样本下即可获得较高的分类精度。该方法首先对高光谱原始数据进行主成分分析(principal component analysis， PCA)，并基于第一主成分通过GLCM提取手工空间特征，将其与原始高光谱数据融合，形成标签样本数据。考虑到3D-CNN中包含大量的待训练参数，为降低参数训练的负担，本文采用不含任何待训练参数且简单易实现的KNN算法来选择一定数量的未标签近邻样本，但未标签样本中同样包含冗余的空间信息，因此通过相关性分析去除相关性较高的成分以降低3D-CNN训练过程中的计算代价。将经过相关性分析之后的近邻未标签样本数据与相应的标签样本数据融合(将未标签样本数据的特征作为标签样本新的特征属性)，作为3D-CNN网络的输入，利用3D-CNN挖掘深层空谱特征。本文高光谱图像分类的总体框架图如图1所示。图1中GLCM-CNN是将GLCM算法所提取的空间特征与原始数据相结合，然后将其输入至CNN网络。

图1 本文高光谱分类方法框架图

1.2 GLCM算法

纹理特征是通过特征提取算法计算出来的一组度量，用来量化图像的感知纹理[8]。纹理特征通常在移动窗口中计算，为图像中的每一个像元设置一个明确和通用的邻域集[16]。GLCM方法就是通过统计图像中每个像元及其邻域的灰度属性来提取图像的纹理特征信息，即对图像上的分别具有某个灰度值的2个像元在给定偏置距离状况下出现的频率进行统计，它列出了像元对在不同灰度值下出现的联合概率分布。一般地，在计算GLCM的过程中，取位移过程中为0°、45°、90°、135°的4个方向角，然后对4个方向的特征值取平均值作为纹理特征值矩阵。从GLCM中计算得到纹理特征，本文从中提取了8个纹理标量形成纹理特征波段，分别为均值、方差、同质度、对比度、相异性、熵、角二阶矩、相关性。

1.3 3D-CNN

如何找到有效的特征是图像分类和模式识别中的核心问题。与基于谱特征的1D-CNN和基于空间特征的2D-CNN相比，基于空谱联合特征的3D-CNN在一定程度上兼顾了二者的优势，即同时自发地提取高光谱图像中的光谱信息和空间信息。通过无监督的方式进行初始化，然后以有监督的方式进行微调，不断从低层次特征中学习具有抽象性和不变性的高层次特征，有利于分类、目标检测等多种任务。

在高光谱图像分类中，3D-CNN可以将输入的HSI像素映射到输入像素标签，从而HSI中每个像素点都可通过网络来获得其类别标签，完成对HSI进行像素级分类的目的。相对而言，3D-CNN是从以某一像素点为中心像素点的小空间邻域的立方体中提取空谱信息，将输出层得到的类别标签作为中心像素点的标签。因此，3D-CNN的输入为从HSI中提取出的三维立体像素块，像素块大小为K×K×B。其中K为像素块的空间维大小，必须为奇数，B则是像素块在光谱维的大小，为原始HSI的波段数。3D-CNN的计算可用式(1)表示。

(1)

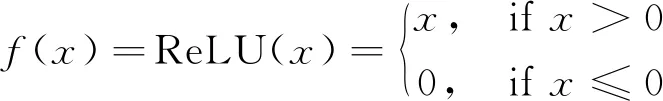
(2)

另外，本文采用自适应矩估计(adaptive moment estimation，Adam)算法作为梯度优化算法[17]。该算法结合了AdaGrad算法善于处理稀疏梯度和RMSProp算法善于处理非平稳目标的优点，利用梯度的一阶矩估计和二阶矩估计，动态地调整每个参数的学习率，经过偏置校正后，为不同的参数进行更新，具体表达如下。

首先，假设在t时刻，目标函数对于参数的一阶导数为gt。式(3)和式(4)是对梯度的有偏一阶矩估计和有偏二阶矩估计的更新，根据梯度通过式(5)和式(6)进行偏差修正，最后通过式(7)完成对参数的更新。

mt=β1mt-1+(1-β1)gt

(3)

(4)

(5)

(6)

(7)

式中：β1和β2为矩估计的指数衰减速率，分别为0.9和0.999；mt和vt为t时刻的一阶矩和二阶矩变量，初值均为0；η为学习率。为了防止分母为0，设置一个值为10-8小常数ε；θt为t时刻的3D-CNN参数变量，包含权重和偏置。

1.4 算法描述

具体的算法实现描述如下。

开始 1)特征提取。输入:原始HSI。①通过PCA算法对原始数据集进行主成分分析,取第一主成分PC;②根据GLCM算法,将滑动窗口在PC上按步长d和方向角滑动,每滑动一次计算该滑动窗口的灰度共生矩阵,并求得纹理特征值,将该窗口的纹理特征值赋值给窗口的中心像素;③重复步骤②,直到滑动窗口覆盖PC;④对某一纹理标量,将4个方向角下的某一纹理特征矩阵进行求和取平均,作为该纹理特征最终的纹理特征矩阵,其他纹理特征亦是如此;⑤重复步骤④,直至获得8个纹理特征;⑥特征提取完毕。输出:纹理特征。2)近邻未标签样本选择。输入:原始HSI。①对于原始数据中某一标签样本,计算其与所有未标签样本的欧式距离,并按升序排列;②重复步骤①,直到计算完所有标签样本;③所有标签样本的近邻样本提取完毕。输出:标签样本与未标签样本的近邻关系序列。3)输入数据预处理。输入:原始HIS、阶段1提取的纹理特征、阶段2输出的近邻关系序列。(1)标签样本。①将标签样本在阶段1特征提取中提取的空间特征作为新的特征属性,与原始数据进行融合;②标签样本数据获取完成。(2)未标签样本。①对未标签样本在阶段1特征提取中提取的空间特征进行相关性分析,剔除相关性较高的成分,获得空间特征;②未标签样本数据获取完成;③按照阶段2中的近邻关系,将a中的标签样本数据与b中未标签样本数据进行融合;④输入数据获取完成。输出:CNN的输入数据。4)3D-CNN。输入:阶段3获取的CNN的输入数据。将输入数据按训练策略随机分为训练样本和测试样本,每个样本的输入大小均为K×K×B。(1)训练阶段。①每次从训练样本中随机输入batch(batch=20)个训练样本到预先建立好的3D-CNN网络中进行训练;②假设第一层包含n个大小为C×C×D的卷积核,每个K×K×B大小的样本经过第一层的卷积运算后,则会输出n个(K-C+1)×(K-C+1)×(B-D+1)大小的数据立方体;第一层的输出作为第二层的输入,继续进行卷积运算(类似于第一层);如此类推,最终的输出被转换成一个特征向量输入进全连接层,将卷积过程中提取的局部特征映射融合,经Softmax交叉熵函数计算损失率后,通过反向传播计算每个参数的梯度,利用Adam算法动态地更新网络参数;③重复步骤①、②,直到完成预设定的迭代次数;④模型训练完毕。(2)测试阶段。①将测试样本输入到已训练好的3D-CNN模型中,根据预测标签与真实标签,计算混淆矩阵,并得到分类精度;②测试完成。5)输出混淆矩阵、总体分类精度、平均分类精度、Kappa。结束

2 实验结果与讨论

为了验证该方法的有效性，将它与3D-CNN和GLCM-CNN分类方法进行对比，并在3个被广泛使用的不同环境的高光谱数据集上进行评估。文中所有分类算法的实验结果均采用总体精度(overall accuracy， OA)、平均精度(average accuracy， AA)和Kappa值(kappa statistic， K)来评估，实验结果形式为平均值±标准差。

2.1 数据描述

1)Salinas数据集。Salinas数据集是1992年由AVIRIS(airborne visible/infrared imaging spectrometer)传感器在美国加利福尼亚州Salinas山谷采集的，图像大小为512像素×217像素，包含224波段，其空间分辨率为3.7 m。在去除吸水率和低信噪比波段后，使用204个波段进行分析。数据中共含有16个不同的类别，其图像和地面真值如图2所示，样本信息见表1。

图2 Salinas数据

表1 Salinas数据集中的类别和样本(像素)量

2)Indian数据集。Indian数据集是由NASA的AVIRIS仪器于1992年在印第安纳州西北部采集获得。Indian数据共包含224个波段，图像大小为145像素×145像素，空间分辨率为20 m。去除吸水率和低信噪比波段后，使用220个波段进行分析。该地点定义了16个类别，代表在此环境中产生的各种土地覆盖类型，其对应图像和类别信息分别如图3和表2所示。

图3 Indian数据

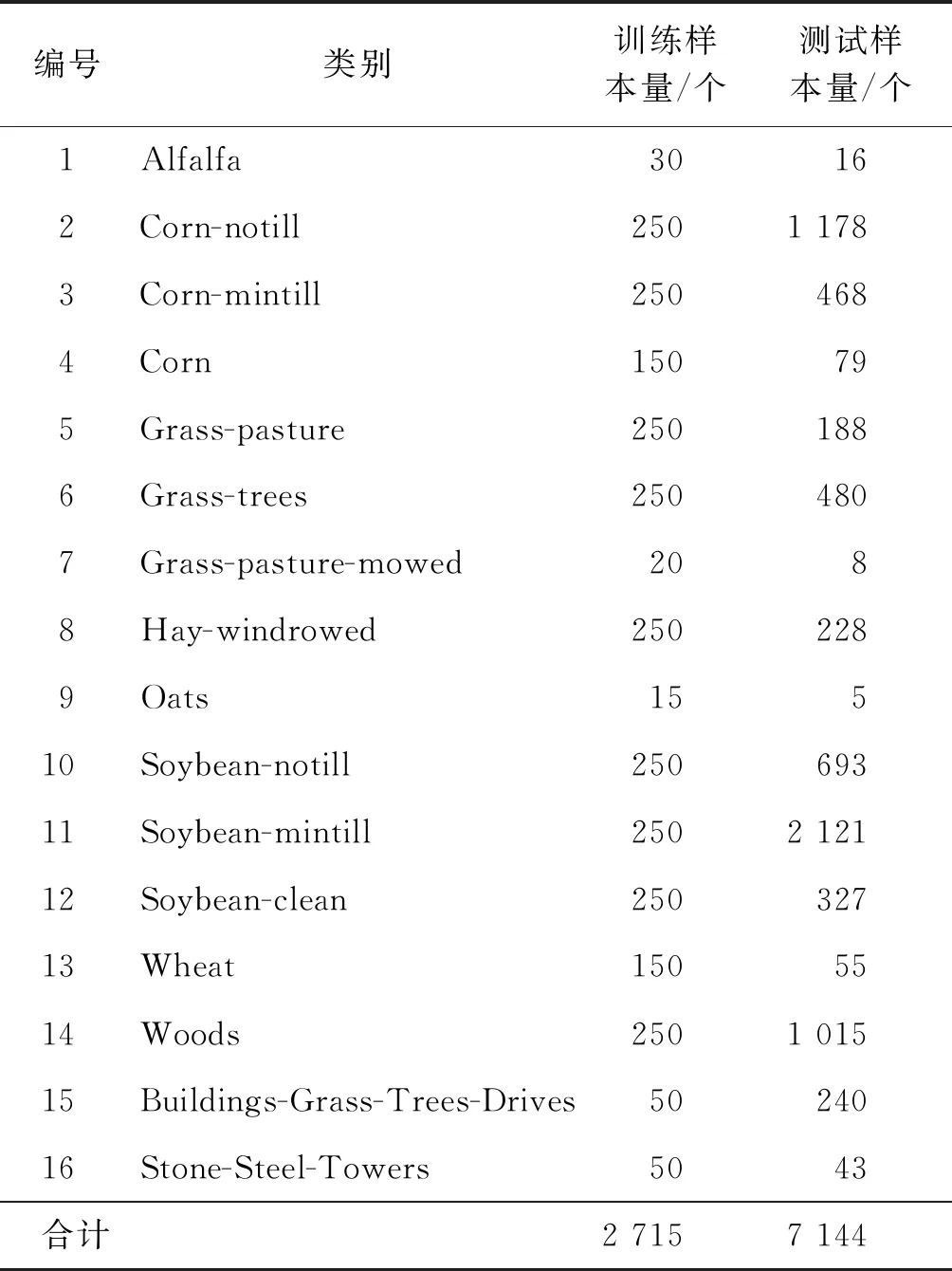
表2 Indian数据集中的类别和样本(像素)量

3)Pavia University数据集。第3个数据集是2001年在意大利北部Pavia大学由ROSIS传感器(reflective optics system imaging spectrometer)收集的。采集到的数据由115个波段组成，分辨率为1.3 m。在去除了覆盖吸水率的无隔音带和噪声带之后，只使用了103个波段。本文所使用的原始数据由610像素×340像素组成，包含了9种土地覆盖类别，如图4和表3所示。

图4 Pavia University数据

表3 Pavia University数据集中的类别和样本(像素)量

2.2 网络设计与实验设置

CNN中包含大量待训练参数，而网络的结构直接影响训练参数的多少，结构越复杂，训练参数越多，同时需要训练出成熟稳定的模型所耗时间也就越多。本文通过GLCM算法从第一主成分波段提取8个纹理特征，其中滑动窗口的大小均为5×5。对于近邻未标签样本的空间信息，采用相关性分析的方法，去除纹理特征中相关性较大的成分。表4、表5、表6分别为Salinas、Indian、Pavia University 3个数据集的纹理特征相关系数矩阵。在通过相关系数矩阵进行相关性分析时，有时需要去除冗余的变量成分。2个变量相关性较大时，可以对比变量与其他变量的相关性，保留整体相关性较小的变量。当2个纹理特征高度相关(相关系数绝对值大于0.8)时，则选择平均绝对相关性(average absolute correlation， AAC)[2]较小的纹理成分进一步研究。某一特征的AAC为该特征与其他特征(含该特征本身)的相关系数绝对值和的平均。例如，表4中，Hom(同质度)与Ent(熵)之间的相关系数为-0.931 1，Hom的平均绝对相关值为0.583 2，Ent的平均绝对相关值为0.561 9，则去除高相关成分Hom。因此最终Salinas数据集中保留的纹理成分为均值(Mea)、方差(Var)、对比度(Con)、相异性(Dis)、角二阶矩(ASM)、相关性(Cor)。Indian数据集保留的纹理成分为均值(Mea)、方差(Var)、熵(Ent)、角二阶矩(ASM)、相关性(Cor)。Pavia University数据集保留的纹理成分为均值(Mea)、对比度(Con)、角二阶矩(ASM)、相关性(Cor)。

表4 Salinas数据集的纹理特征相关矩阵

表5 Indian数据集的纹理特征相关矩阵

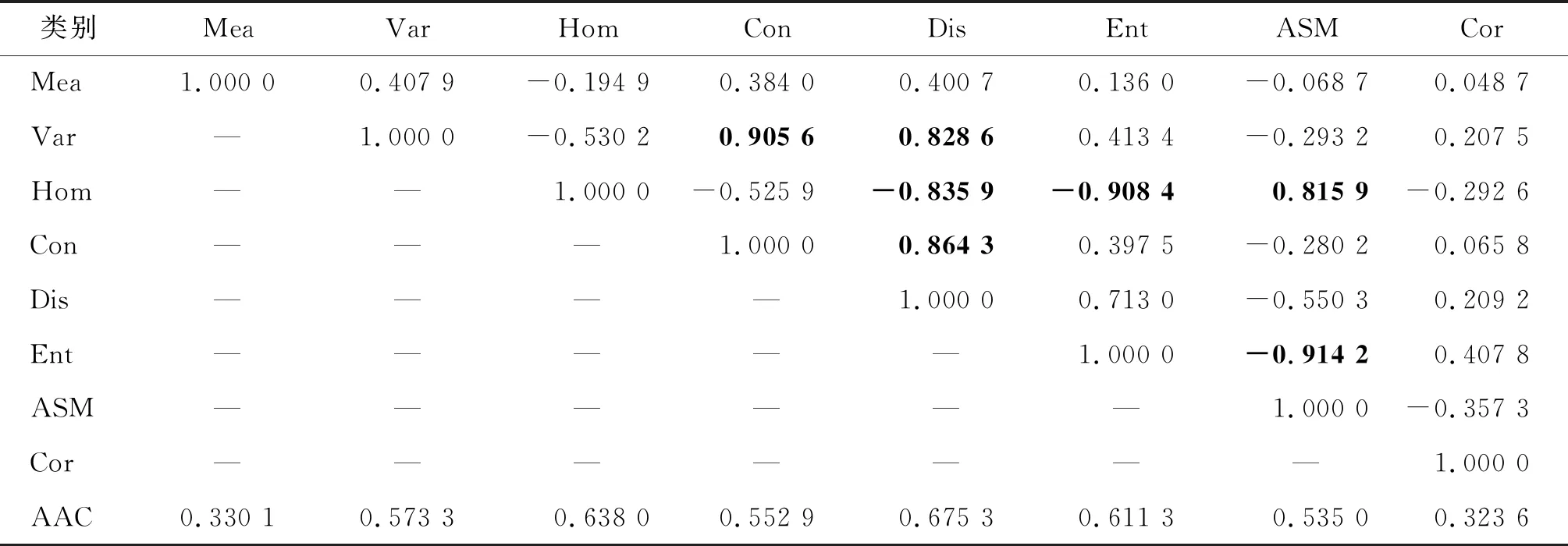
表6 Pavia University数据集的纹理特征相关矩阵

文献[13]中所提出的模型更轻量，且易训练、易调参，我们借鉴了其模型优势，并在算法和模型上加以改进。在本文中，网络的输入统一设置为邻域大小为5×5×B的三维数据块，B为输入的波段数。在近邻未标签样本的选择中，通过实验分别为Salinas、Indian、Pavia University 3个数据集中每个标签样本选择1、2、3个未标签样本。最终Salinas数据集的输入大小为5×5×218，其中218=204+8+6×1，类似地，Indian数据集的输入大小为5×5×218，Pavia University数据集的输入大小为5×5×123。每种分类方法均在随机选择训练样本的前提下重复5次，将5次实验结果累加求平均后的结果作为最终分类结果。根据输入大小对所设计网络的超参数进行微调，最终的网络结构包含2层卷积层，1层Dropout层，1层全连接层以及输入层和输出层，最后通过Softmax分类器和交叉熵代价函数训练模型。将输入数据归一化至[0， 1]，模型的学习率设置为0.001，Dropout值为0.5，批量输入网络的数据量大小为20，Salinas、Indian、Pavia University 3个数据集的训练迭代次数分别设置为15 000、6 000、20 000。3个数据集的网络结构如表7、表8、表9所示。

表7 Salinas数据集的网络结构

表8 Indian数据集的网络结构

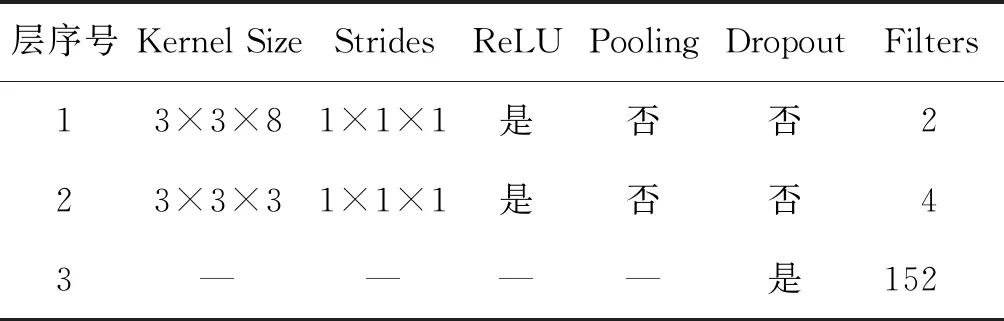
表9 Pavia University数据集的网络结构

2.3 实验结果

1)Salinas数据集分类结果。表10是3种分类算法在Salinas数据集上的分类结果，图5为对应的分类结果图，可以看出本文所提出的算法取得了较好的分类性能。三维卷积神经网络具有同时提取深光谱-空间信息的特点，相较于3D-CNN、GLCM-CNN在原始高光谱图像中提取纹理特征，进一步增强了空间信息，取得了较好的分类结果。而本文方法在保留标签样本光谱-空间信息的基础上，通过引入近邻的未标签样本的纹理特征，提高了随机抽取训练样本过程中的样本质量，同时提取标签样本与未标签样本的深层特征，增强了训练样本信息的多样性。表10中，本文方法取得了更高的分类精度值，相较于3D-CNN、GLCM-CNN，整体分类精度分别提高了4.92%、2.52%，Kappa值分别提高了5.45%、2.89%。对于类别8、9、10，本文方法比GLCM-CNN分别提高了3.71%、2.38%、1.31%。另外,本文方法OA的标准差为0.445 8，相较于3D-CNN和GLCM-CNN，本文方法的整体分类结果离散程度较小，体现了该方法的稳定性，表明未标签样本信息的引入有效降低了噪声样本在训练过程中产生的影响。

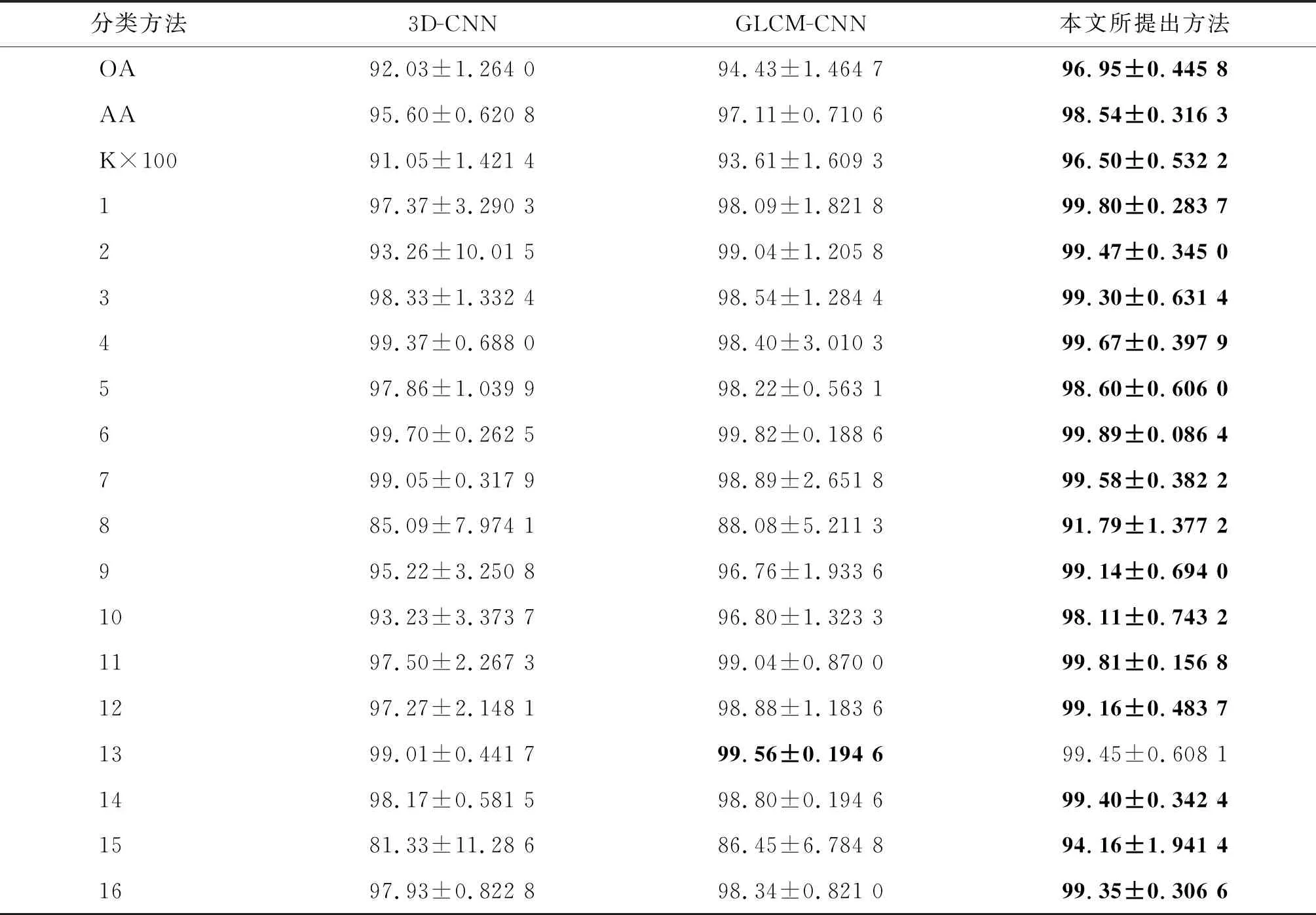
表10 Salinas数据集的分类结果 %

图5 Salinas数据分类结果图

2) Indian数据集分类结果。Indian数据集的分类结果如表11和图6所示。与其他分类算法相比，本文提出的算法均获得了最高的OA、AA、Kappa，进一步说明了本文算法的优越性。表11中，除类别3和类别7之外，类别5、6、8、13都获得了与GLCM-CNN接近的精度，其他类别的分类精度都得到了一定提升。例如相较于GLCM-CNN，本文方法中类别11和类别15分别提高了5.10%、6.18%。从整体分类结果来看，引入近邻未标签样本的信息适用于大多数类别，验证了该策略的有效性。而且，从分类结果图上看，本文方法有效地抑制了噪声点，分类结果图像更加平滑，对不同类间边缘区域的区分更加精细。

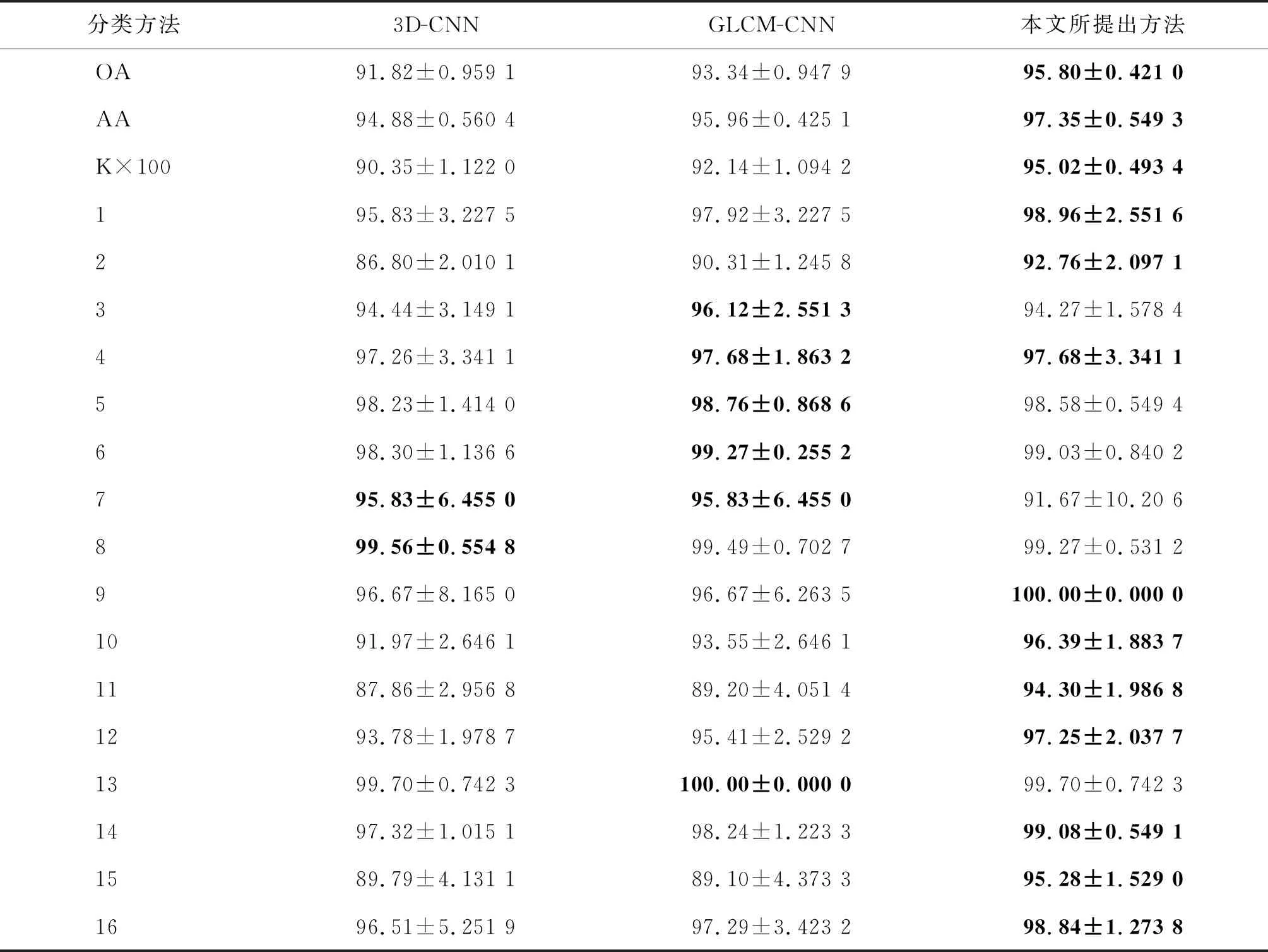
表11 Indian数据集的分类结果 %

图6 Indian数据分类结果图

3) Pavia University数据集分类结果。表12是Pavia University数据集的分类结果，其可视化分类结果如图7所示。与前2个数据类似，本文算法同样取得了最好的分类性能。GLCM-CNN算法所提取的纹理特征增强了空间信息，但与3D-CNN相比，在个别类别上仍有不足。而本文算法在GLCM-CNN分类方法的基础之上，结合未标签样本的多样性信息之后进一步提取深层特征，有效缓解了Hughs现象，体现了该算法的有效性和普适性。

表12 Pavia University数据集的分类结果 %

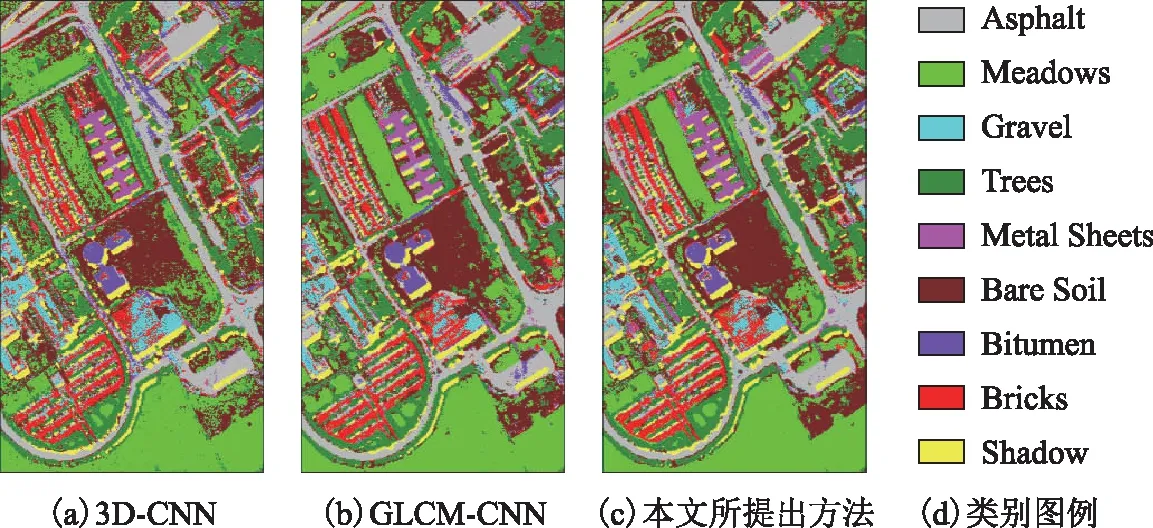
图7 Pavia University数据集分类结果图

2.4 参数的影响

1)训练样本数量的影响。在CNN的训练过程中，训练样本的数量是非常重要的因素。由于CNN中包含大量的待训练参数，需要大量的训练样本来保证样本的多样性，以提取更具有健壮性和有效性的特征。而对HSI来说，由于其地物标签获取的代价高以及大量未标注样本，如何通过少量样本来获取更高的分类精度是HSI分类领域中的重点和难点。

在本节讨论了3个数据集在不同训练样本比例下的分类精度，其结果如图8所示。通过图8可以发现，随着训练样本比例的增加，分类精度呈增长趋势。对于Salinas和Pavia University数据集，分别对比了每类训练样本在100至300个像素点和100至500个像素点的总体分类准确率的情况。对于Indian数据集则在训练样本比例为10%至50%时进行了分析。在3个数据集中，本文分类方法在不同数量或比例的训练样本下均优于其他分类方法。对于Salinas数据集，本文方法在每类训练样本为200个像素点时，整体分类精度为94.25%，略小于GLCM-CNN在每类训练样本量为300个像素时的精度(94.43%)。在Indian数据集中，本文算法中训练样本比例在30%(OA=98.09%)就超过了其他算法在50%(如GLCM-CNN，OA=97.76%)训练样本比例下的精度。因此相较来看，相同条件下，本文算法可以获得更高的精度；而获得相同的精度，本文算法则需要较少的训练样本，从而可以减少标注成本。

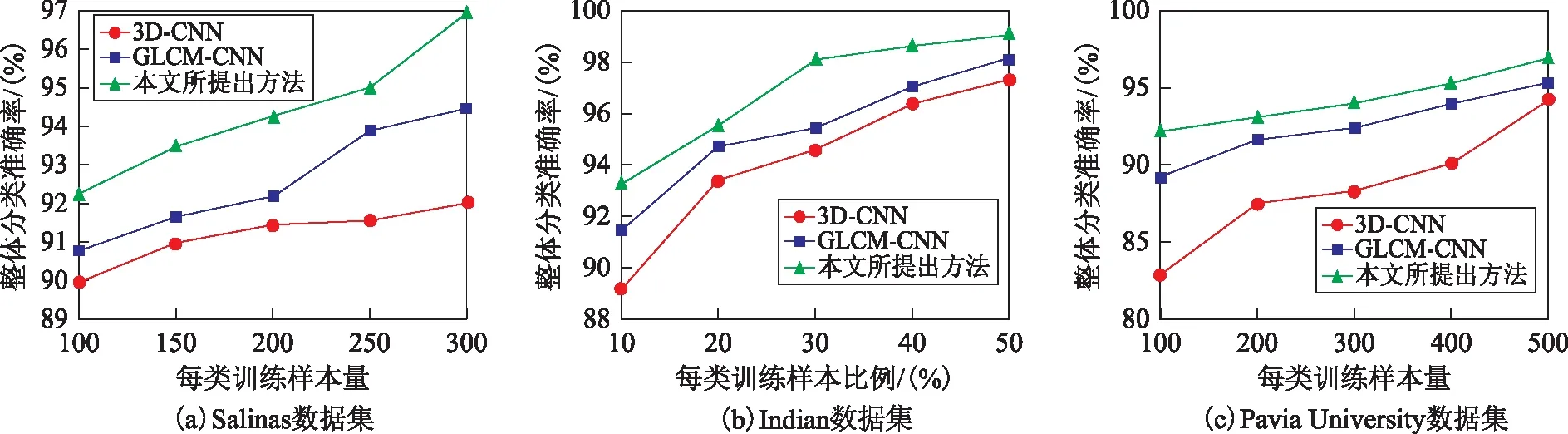
图8 训练样本数量的影响

2)GLCM滑动窗口大小的影响。GLCM算法通过在一定大小的滑动窗口中提取空间纹理信息，滑动窗口的不同影响特征的提取，而且计算代价随着窗口大小的增大而增大。为了选取合适的滑动窗口，本节选取了3×3、5×5、7×7 3种大小的窗口应用于3个数据集进行了探究，结果如表13、表14、表15所示。表14中，Indian数据集在窗口为5×5下达到了最高分类精度，而Salinas数据集和Pavia University数据集均在窗口大小为7×7时分类效果最好。综合3个数据集来看，窗口大小为5×5时优于3×3的分类结果，而窗口7×7与5×5时的分类精度相差较小。为综合考虑计算时间与样本信息问题，本文算法中滑动窗口大小为采用5×5。

表13 不同滑动窗口下的Salinas数据的分类结果 %

表14 不同滑动窗口下的Indian数据的分类结果 %

表15 不同滑动窗口下的Pavia University数据的分类结果 %

3)近邻样本数量的选择。KNN算法中不包含任何待训练参数，只有近邻样本数量的选取对结果产生影响。针对不同场景下的数据集，本文通过实验选择合适的近邻未标签样本的数量。本节主要探究了近邻样本量处于1至10时对本文算法的影响。如图9所示，随着近邻样本数量的增多，Indian数据集和Pavia University数据集的分类精度值呈先升后降的趋势，Salinas数据集整体呈下降趋势，表明在地物类别较复杂的场景，少量近邻未标签样本的引入有益于分类精度的提高，当未标签样本数量较多时，引起了Hughs现象，而且近邻样本的增多，也意味着CNN网络训练过程中的时间代价的增大，因此选择合适的近邻样本量需要综合考虑分类精度和模型的计算复杂度。本文使用的Salinas、Indian和Pavia University 3个数据集中，选择的近邻未标签样本量分别为1、2、3。

图9 近邻样本数量的选择

3 结束语

为充分挖掘标签样本的空间信息，本文采用GLCM算法增强空间特征和融合近邻样本信息的策略，提出了利用未标签样本的基于GLCM算法与3D-CNN算法的高光谱遥感图像分类方法，并将该方法与3D-CNN和GLCM-CNN方法进行了对比分析。实验结果表明，本文建议的方法可在较少的训练样本下，在总体上获得较优的分类性能。

通过GLCM算法可以有效地提取空间纹理信息。由于不同地物类别的敏感纹理特性有所不同，利用3D-CNN算法可以进一步深度挖掘空谱联合特征，适用HSI的三维数据结构和数据特征。同时利用高光谱图像中大量的未标签样本不但可以降低样本噪声，丰富样本信息，更可以减少CNN训练过程中对标签样本数量的需求。对于引入未标签样本信息所带来的额外的时间代价，通过相关性分析可以去除冗余特征，有效降低计算成本，获得更好的分类效果，为高光谱遥感图像分类提供了一种新的方法。