一类含有扰动项的常p-Laplace Hamilton系统周期解的存在性

黄丽丽

（吉首大学师范学院，湖南吉首 416000）

1 主要结果

本文考虑如下系统

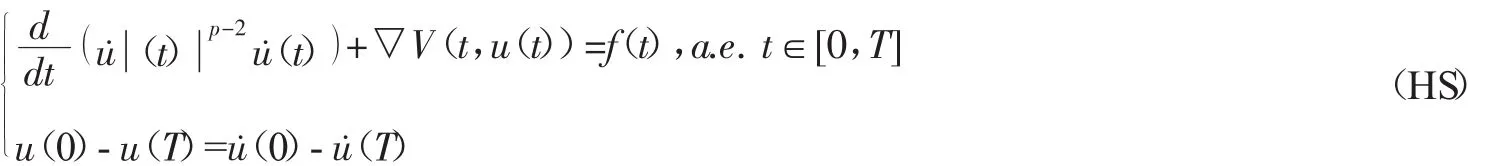
周期解的存在性，其中p＞1，V∶[0，T]×RN→R，f∈L1（[0，T]；RN），▽V（t，x）是V关于x的梯度，且V满足如下假设

（A）对∀x∈RN，V（t，x）关于t可测，对于a.e.t∈[0，T]，V（t，x）关于x连续可微，且存在a∈C（R+，R+），b∈L1（[0，T]；R+）使得

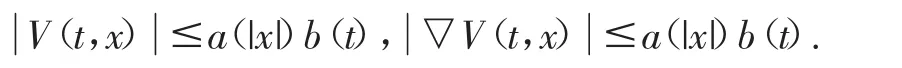
大多数学者研究了p=2且f=0的情形，见文献[1-3]，文献[4]和[5]研究了f=0的情形，本文受文献[4]和[5]的启发，利用鞍点定理研究系统（HS）在文献[5]中的局部渐进p-二次条件下的周期解的存在性，推广了文献[5]的结果，得到新的存在性定理.

定理1.1 若V满足（A）及以下条件

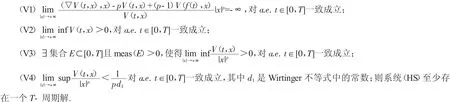
2 预备知识

又由文献[6]可设系统（HS）对应的泛函为

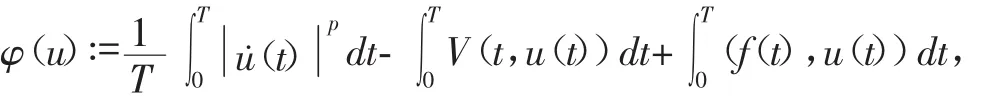
易知其是连续可微的，且其临界点对应系统（HS）的T-周期解，且对∀u，v∈W1，pT有

定义2.1[6]设X是实Banach空间，φ∈C1（X，R），若{un}⊆X，φ（un）有界，φ′（un）→0（n→∞）蕴含{un}有收敛的子列，则称φ满足Palais-Smale条件（简称PS条件）.

定义2.2[6]设X是实Banach空间，φ∈C1（X，R），若{un}⊆X，φ（un）有界，||φ（un）||（1+||un||）→0（n→∞）蕴含{un}有收敛的子列，则称φ满足Cerami条件（简称C条件）.

定理2.1[7]（Fatou引理）若｛fk（x｝）是E上的非负可测函数列，则

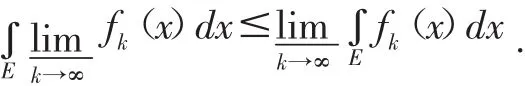
定理2.2[8]（鞍点定理）设X是实的Banach空间，φ∈C1（X，R），X=X1⊕X2，X1≠{0}是X的有限维子空间，若φ∈C1（X，R）满足（PS）条件以及：

则φ在X上必有临界点.

注2.1 鞍点定理在更弱的C条件下仍然成立，见文献[8].

3 定理1.1的证明

第一步，证明φ满足C条件.令{φ（un）}是空间中的C序列，则存在常数L＞0，使得对任意的n∈N有

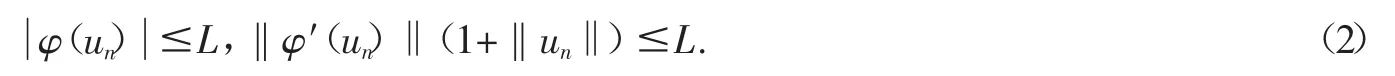
由（V2）可知存在常数 M1＞0，使得对所有的|x|≥M1，a.e.t∈[0，T]有

又由（V1）有，对任意的 β＞0，存在常数 M2＞M1＞0，使得对所有|x|≥M2，a.e.t∈[0，T]，有

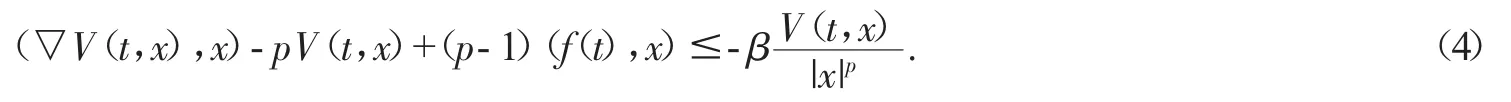
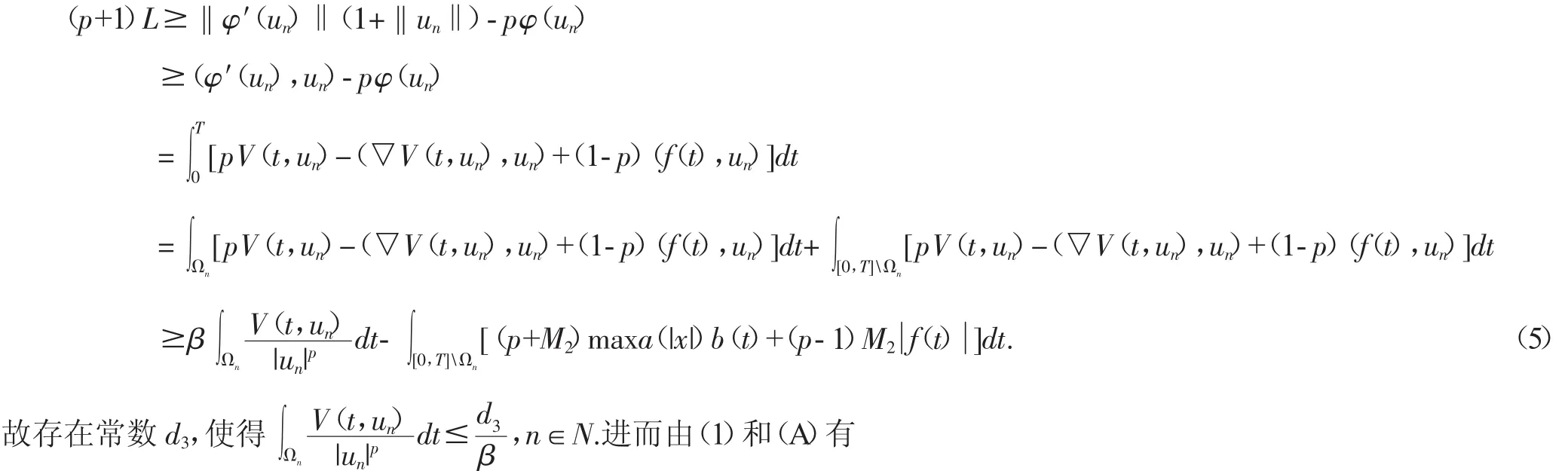
即当 ||u||→+∞ 时，φ（u）→-∞.