让数学课充满生长的力量

○朱宇

传统的以接受定论性知识为主的积累式学习方式，已不能适应当今信息化、智能化的时代。当下的数学学习应该聚焦知识的建构与创生，关注其意义理解与灵活运用，激发学生主动参与、深度思考，促进知识、学力、经验、智慧的生长。

【教学片段】人教版小学数学六年级上册第四单元《比的意义》

（情境导入）播放视频：航天英雄打开神舟七号气闸舱舱门，挥动五星红旗，向全国人民问好。

师：同学们对我国的国旗了解吗？请看大屏幕，航天英雄展示的国旗，长和宽分别是15厘米和10厘米。

师：你会用算式表示长和宽的倍数关系吗？

生：15÷10，10÷15。

师：两个除法算式分别是什么意思呢？

生：长是宽的几倍，宽是长的几分之几。

师：这里长与宽的倍数关系也可以说“长和宽的比是15比10，宽和长的比是10比15”，分别写作“15∶10”和“10∶15”。（板书）

【诊断分析】

上述教学片段从除法的意义入手，借助国旗长与宽的关系，从“两个数相除的倍数关系”迁移得到“两个数相除又叫做两个数的比”。看似浅显易懂，符合小学生的认知水平，但是仅凭国旗的长与宽这一组数据，直接由除法推出比的概念，就能够让学生感受两个有关联的数量之间的关系吗？学生虽然能模仿进行浅层次的复述，但是对“比”的意义有充分理解和感悟吗？学生最大的困惑是：“既然两个数相除又叫做两个数的比，那么，有了除法，为什么还要学习比？”单薄的素材不能驱动学生积极思考和主动探究，深层次的认知也无从实现。

【教学建议】

比的本质是表示两个有关联的数量之间的倍数关系，这种关系是基于某种客观规律而产生的。为此，要链接学生的生活经验，由现实问题启动意义的探索。

可以创设“兑牛奶要放奶粉和开水”的情境，从奶粉与水“1比3”的配比引入，初步体会“比可以表示两个数量之间的关系”。接下来，通过“如果有奶粉10克，要多少克水？20克奶粉呢？40克奶粉呢”等问题的解决，学生发现，“1份奶粉，3份水”“水一直都是奶粉的3倍”“奶粉和水的比是1∶3”，借助分数、份数、倍数来理解比的意义，将新知纳入已有认知经验，实现概念之间关系的沟通。从更长远的角度看，从“兑牛奶”的过程还可以引导学生发现，水和奶粉的变化中存在着某种规律，为比例的学习埋下伏笔。

通过奶粉与水、路程与时间、总价与数量等大量素材的感知，启发学生进行意义的抽象概括：两种数量在什么情况下可以用比来表示它们的关系？直指概念的本质，升华活动中获得的感性认识，促进学生对概念内涵的理解。

【教学片段】人教版小学数学五年级上册第二单元《用数对确定位置》

课件播放：人们在确定位置时，通常把竖排叫做列，横排叫做行。一般情况下，确定第几列从左往右数，确定第几行从前往后数。

师：现在再让你描述小军的位置，你想怎样说呢？

生：第4列第3行。

师：是啊，有了统一的规定，我们表达起来既准确又简洁。请大家再数一数列、数一数行。（学生齐数列与行。）

课件出示小红和小芳的位置，学生用第几列和第几行来交流。

【诊断分析】

上例中，学生以接纳的方式，掌握了用数对确定位置的方法，过程简单而顺畅。然而，在后续学习中，却暴露出诸多问题。例如，用数对表示教室里学生的位置，不能分辨左右，不能体会观察点规定的必要性；从座位图抽象成方格图，学生不理解方格图中“0”的实际意义……究其原因，上例中割裂了经验与新知的关联，没有组织学生通过观察分析、尝试表达、合作交流等方式，从用个性化的生活经验描述位置，逐步发展到用有规则的数学方法确定位置，学生的思维水平没有在经验的不断改造中逐步提升。

【教学建议】

教师应准确把握数学知识的存在基础和发展形态，促进认知结构的有效生长。从确定位置的经验出发，将教材提供的座位图进行适当的加工与整合，产生认知冲突，使学生整体把握知识结构，逐渐深化对数学知识本质的认识和理解。

《用数对确定位置》的教学，其本质是为第三学段平面直角坐标系的学习积累感性经验。因此，在方格图上用数对确定位置是教学重点。教师要引导学生经历确定位置方法的发展过程，结合多样的情境，从一维直线上确定位置开始，自主构建在二维平面中确定位置的方法系统，在比较、优化中深刻理解用数对确定位置的合理规则，感受用数对确定位置所体现的一一对应、数形结合的思想方法。

【教学片段】人教版小学数学二年级上册第六单元《7的乘法口诀》

出示：不计算，直接填出括号里的数。7×6=7×5+（ ）。

生：左边，六七四十二；右边，五七三十五，

42-35=7。

师：请注意，不计算。

（学生沉默，感到很为难。）

师：左边是6个7，右边呢？（指着7×5）

生：5个7。

生：再加上1个7。

师：很好，继续。请看6×7=6×6+（ ）。

生：左边是6个7，右边是6个6，还要加上1个7。

生：不对，应该是加上1个6。

【诊断分析】

该填数练习由“6个7比5个7多（ ），比7个7少（ ）”变化而来，意在通过计算和比较，帮助学生进一步理解相邻两句口诀之间的联系，丰富记忆口诀的方法。解决填数问题，需要借助“几个几”的意义来解释，而且需要从整体上把握等式两边的算式的含义，学生理解起来有一定的困难。这说明，乘法口诀的记忆与应用，死记硬背和机械训练较为常见，容易忽视乘法意义层面上的理解性记忆。所以，即使乘法口诀背熟了，学生对“几个几”的意义仍然生疏。

【教学建议】

出示7×6点子图。

师：从图中你看到几个几？

生：我看到了6个7。

生：我看到了7个6。

师：现在你能看出括号里该填什么吗？7×6=7×5+（），6×7=6×6+（）。

师：不计算，你能直接填写吗？

（一部分学生露出迷茫的神色。）

课件出示经过分割的点子图。

师：现在，对照图你能说一说吗？

生：从第一幅图看出，5个7加1个7，所以7×6=7×5+（7）。

生：从第二幅图看出，6个6加1个6，所以6×7=6×6+（6）。

同一幅7×6的点子图，展现不同的分割方法，借助数形结合的力量，展现数学知识背后丰富的思想方法和思维价值，让知识结构顺利生长。

【教学片段】人教版小学数学五年级上册第六单元《组合图形的面积》

巩固练习环节。

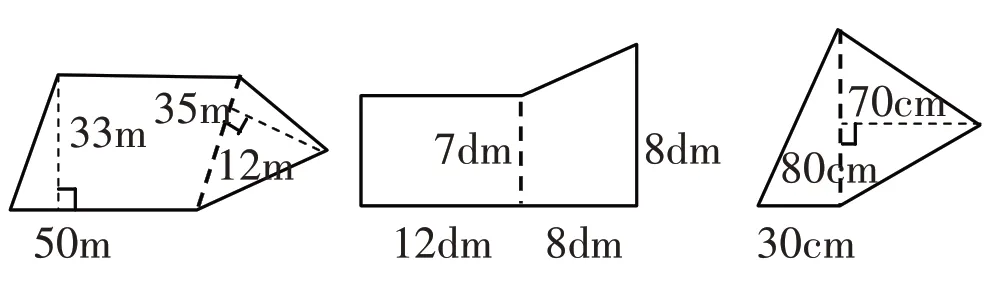
师：这些图形的面积各是多大？你会计算吗？

指名口答第一幅图的面积，然后学生完成后两幅图的面积计算。

【诊断分析】

生活中的组合图形面积计算，数据不会是现成的，测量哪些数据是有讲究的。课堂练习进行面积计算的重复训练，既不能培养学生解决实际问题的能力，也缺失了数学思考的成分。例如，如何对组合图形进行合理的分割或添补？测定哪些数据就可以解决问题？重复机械的练习，不但消解了已形成的探索体验，而且让转化、类比、优化等思想方法的积淀无从落实。

《组合图形的面积》教学主要包括方法的探索归纳与运用拓展。在方法探索环节，学生感知了大量的组合图形，基本图形的面积计算技能基本形成。练习环节就应该从添加辅助线、测量必需数据以及丰富问题背景等方面，设计从易到难、有一定梯度的练习，发展学生的空间想象能力和推理能力，在解决问题中培养学生思维的灵活性。

【教学建议】

教学中，可以从思维材料的组织入手，有意隐去组合图形中的部分数据，使学生由思维冲突引发思考：你觉得至少需要知道几个数据就能算出面积？变“简单机械地练”为“尝试探索着学”，真实的任务促进学习更深入的发生。学生对图形进行了不同的分解，准确锁定所缺少的条件，然后经过观察、分析，测量有效数据，寻求解题途径。最后，学生通过表达、倾听，进行思维碰撞，体会方法的多样性。

通过对思维材料的合理加工，改“成品”为“半成品”，按照“无辅助线，有数据”→“无辅助线，有部分数据”→“既无辅助线，也无数据”的顺序，摒弃重复训练，聚焦数学思考，让筛选、优化、转化等策略成为学生的自发需要，观察、分析、类比、想象、推理等思维方法得到运用，深刻性、灵活性、系统性等思维品质在数学学习过程中得到提升。